rabacus.f2py package¶
Submodules¶
rabacus.f2py.chem_cool_rates module¶
Wrapper to make the fortran calling identical to the python calling.
-
class
rabacus.f2py.chem_cool_rates.ChemistryRates(T, fcA_H2, fcA_He2, fcA_He3, H1i=None, He1i=None, He2i=None, fit_name='hg97', add_He2di=True)[source]¶ A chemistry rates class.
Provides access to collisional ionization and recombination rates as a function of temperature. The user can optionally supply photoionization rates which will become attributes of the returned instance. These chemistry and photoionization rates determine the evolution of the ionization fractions for primordial cosmological chemistry.
Args:
T (array): Temperatures.
fcA_H2 (array): Case A fraction for HII.
fcA_He2 (array): Case A fraction for HeII.
fcA_He3 (array): Case A fraction for HeIII.
Note
The case A fractions, fcA_H2, fcA_He2, and fcA_He3, interpolate between case A and case B recombination rates (0.0 = case B, 1.0 = case A).
Kwargs:
H1i (array): HI photoionization rate.
He1i (array): HeI photoionization rate.
He2i (array): HeII photoionization rate.
fit_name (string): Source of rate fits {
hg97}add_He2di (bool): If true, reHe2di is added to reHe2.
Attributes:
u (
Units): Units.ciH1 (array): HI collisional ionization rate.
ciHe1 (array): HeI collisional ionization rate.
ciHe2 (array): HeII collisional ionization rate.
reH2 (array): HII radiative recombination rate.
reHe2 (array): HeII radiative recombination rate.
reHe3 (array): HeIII radiative recombination rate.
reHe2di (array): HeII dielectronic recombination rate.
-
class
rabacus.f2py.chem_cool_rates.CoolingRates(T, fcA_H2, fcA_He2, fcA_He3, H1h=None, He1h=None, He2h=None, fit_name='hg97', add_He2di=True)[source]¶ A cooling rates class.
Provides access to collisional ionization, collisional excitation, recombination, bremsstrahlung, and inverse compton cooling rates as a function of temperature. The user can optionally supply photo-heating rates which will become attributes of the returned instance. These cooling and photo-heating rates determine the evolution of temperature in cosmological gas.
Note
For compton and bremsstrahlung cooling, only the temperature dependent part of rates are stored. See the functions
return_cooling()andreturn_heating()for the proper multiplicative factors.Note
The case A fractions, fcA_H2, fcA_He2, and fcA_He3, interpolate between case A and case B recombination rates (0.0 = case B, 1.0 = case A).
Args:
T (array): Temperatures.
fcA_H2 (array): Case A fraction for HII.
fcA_He2 (array): Case A fraction for HeII.
fcA_He3 (array): Case A fraction for HeIII.
Kwargs:
H1h (array): HI photoheating rate.
He1h (array): HeI photoheating rate.
He2h (array): HeII photoheating rate.
fit_name (string): Source of rate fits {‘hg97’}
add_He2di (bool): If true, recHe2di is added to recHe2.
Attributes:
u (
Units): Units.cicH1 (array): HI collisional ionization cooling rate.
cicHe1 (array): HeI collisional ionization cooling rate.
cicHe2 (array): HeII collisional ionization cooling rate.
cecH1 (array): HI collisional excitation cooling rate.
cecHe1 (array): HeI collisional excitation cooling rate.
cecHe2 (array): HeII collisional excitation cooling rate.
recH2 (array): HII radiative recombination cooling rate.
recHe2 (array): HeII radiative recombination cooling rate.
recHe3 (array): HeIII radiative recombination cooling rate.
recHe2di (array): HeII dielectronic recombination cooling rate.
compton (array): Inverse Compton scattering cooling rate.
bremss (array): Bremsstrahlung radiation cooling rate.
-
return_cooling(nH, nHe, x, z, Hz=None)[source]¶ Returns a cooling rate in erg/(s cm^3).
Args:
nH (array): Number density of hydrogen.
nHe (array): Number density of helium.
x (ionization fractions): An object which contains ionization fractions. For example, instances of the classes in
ion_solver.z (float): Redshift.
Kwargs:
Hz (float): Hubble parameter at z if Hubble cooling is desired.
-
return_heating(nH, nHe, x)[source]¶ Returns a heating rate in erg/(s cm^3).
Args:
nH (array): Number density of hydrogen.
nHe (array): Number density of helium.
x (ionization fractions): An object which contains ionization fractions. For example, instances of the classes in
ion_solver.
-
rabacus.f2py.expint module¶
rabacus.f2py.ion_solver module¶
Wrapper to make the fortran calling identical to the python calling.
-
class
rabacus.f2py.ion_solver.Solve_CE(kchem)[source]¶ Calculates and stores collisional ionization equilibrium (i.e. all photoionization rates are equal to zero) given a chemistry rates object. This is an exact analytic solution.
Args:
kchem (ChemistryRates): Chemistry ratesKwargs:
fpc (bool): If True, perform floating point error correction.Attributes:
T (array): temperature
T_floor (float): minimum possible input temperature
H1 (array): neutral hydrogen fraction,
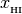 =
= 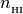 /
/ 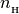
H2 (array): ionized hydrogen fraction,
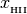 =
= 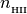 /
/ 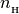
He1 (array): neutral helium fraction,
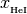 =
= 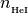 /
/ 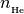
He2 (array): singly ionized helium fraction,
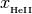 =
=  /
/ 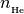
He3 (array): doubly ionized helium fraction,
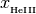 =
=  /
/ 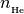
Notes:
This class finds solutions (H1, H2, He1, He2, He3) to the following equations
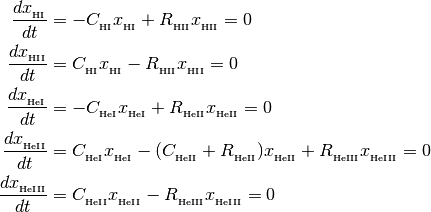
with the following closure relationship
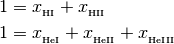
where the
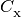 are collisional ionization rates and the
are collisional ionization rates and the
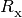 are recombination rates. These solutions depend only
on temperature.
are recombination rates. These solutions depend only
on temperature.Examples:
The following code will solve for collisional ionization equilibrium at 128 temperatures equally spaced between 1.0e4 and 1.0e5 K using case A recombination rates for all species:
import numpy as np import rabacus as ra N = 128 T = np.logspace( 4.0, 5.0, N ) * ra.u.K fcA_H2 = 1.0; fcA_He2 = 1.0; fcA_He3 = 1.0 kchem = ra.ChemistryRates( T, fcA_H2, fcA_He2, fcA_He3 ) x = ra.Solve_CE( kchem )
See also
-
set(kchem)[source]¶ This function is called when a new instance of
Solve_CEis created. Updated ionization fractions can be calculated by calling it again with a new kchem object.Args:
kchem (ChemistryRates): Chemistry rates
-
-
class
rabacus.f2py.ion_solver.Solve_PCE(nH, nHe, kchem, tol=1e-08)[source]¶ Calculates and stores photo collisional ionization equilibrium given the density of hydrogen and helium plus a chemistry rates object. This is an iterative solution. The density and temperature arrays must have the same size and the output arrays are 1-D of that size.
Note
The user must pass in photoionization rates for each species when creating the chemistry rates object (see examples below).
Args:
nH_in (array): number density of hydrogen
nHe_in (array): number density of helium
kchem (
ChemistryRates): Chemistry ratesKwargs:
tol (float): convergence tolerance, abs(1 - ne_new / ne_old) < tolAttributes:
nH (array): H number density.
nHe (array): He number density.
ne (array): electron number density
T (array): temperature
T_floor (float): minimum possible temperature
H1 (array): neutral hydrogen fraction,
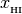 =
= 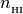 /
/ 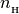
H2 (array): ionized hydrogen fraction,
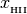 =
= 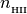 /
/ 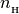
He1 (array): neutral helium fraction,
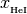 =
= 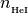 /
/ 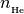
He2 (array): singly ionized helium fraction,
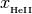 =
=  /
/ 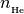
He3 (array): doubly ionized helium fraction,
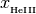 =
=  /
/ 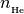
Hatom (
Hydrogen): H atomitr (int): number of iterations to converge
ne_min (array): electron density in collisional equilibrium
ne_max (array): electron density for full ionization
xH1_ana (array): analytic H neutral fraction (neglects electrons from elements other than H)
ne_ana (array): electron number density implied by xH1_ana
x_ce (
Solve_CE): the collisional equilibrium solutions.Notes:
This class finds solutions (H1, H2, He1, He2, He3) to the following equations
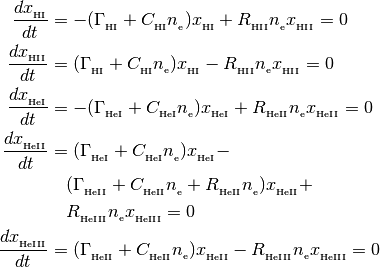
with the following closure relationships
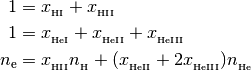
where the
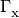 are photoionization rates, the
are photoionization rates, the
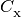 are collisional ionization rates and the
are collisional ionization rates and the
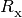 are recombination rates. These solutions depend on
temperature and density.
are recombination rates. These solutions depend on
temperature and density.Examples:
The following code will solve for photo-collisional ionization equilibrium at 128 density-temperature pairs using recombination rates half way between case A and case B for all species. Note that the photoionization rate arrays are grouped with the chemistry rates and so should always be the same size as the temperature array:
import numpy as np import rabacus as ra fcA_H2 = 0.5; fcA_He2 = 0.5; fcA_He3 = 0.5 N = 128; Nrho = NT = N; Yp = 0.24 nH = 10**np.linspace( -4.0, -3.0, Nrho ) / ra.U.cm**3 nHe = nH * 0.25 * Yp / (1-Yp) T = 10**np.linspace( 4.0, 5.0, NT ) * ra.U.K H1i = np.ones( NT ) * 8.22e-13 / ra.U.s He1i = np.ones( NT ) * 4.76e-13 / ra.U.s He2i = np.ones( NT ) * 3.51e-15 / ra.U.s kchem = ra.f2py.ChemistryRates( T, fcA_H2, fcA_He2, fcA_He3, H1i=H1i, He1i=He1i, He2i=He2i ) x = ra.f2py.Solve_PCE( nH, nHe, kchem )
See also
-
class
rabacus.f2py.ion_solver.Solve_PCTE(nH, nHe, kchem, kcool, z, Hz=None, tol=1e-08)[source]¶ Stores and calculates photo-collisional-thermal ionization and temperature equilibrium given the density of hydrogen and helium plus chemistry and cooling rate objects. In other words, a self-consistent equilibrium temperature and ionization state will be found for the input density and redshift. This is an iterative solution. All input arrays should be 1-D. Note that the temperature arrays in kchem and kcool will be altered. It is not important which temperatures are used to initialize the objects kchem and kcool. It IS important that you initialize them with photoionization and photoheating rates. Because we are searching for one temperature for each density all input arrays must have the same shape.
Note
The user must pass in photoionization rates for each species when creating the chemistry rates object and photoheating rates for each species when creating the cooling rates object (see examples below).
Args:
nH (array): number density of hydrogen
nHe (array): number density of helium
kchem (
ChemistryRates): chemistry rateskcool (
CoolingRates): cooling ratesz (float): Redshift. Important for Compton cooling
Kwargs:
Hz (float): Hubble parameter at z if Hubble cooling is desired.
tol (float): convergence tolerance, abs(1 - ne_new / ne_old) < tol
Attributes:
nH (array): H number density.
nHe (array): He number density.
ne (array): electron number density
T_floor (float): minimum possible temperature
H1 (array): neutral hydrogen fraction,
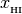 =
= 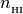 /
/ 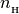
H2 (array): ionized hydrogen fraction,
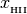 =
= 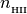 /
/ 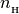
He1 (array): neutral helium fraction,
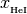 =
= 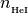 /
/ 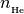
He2 (array): singly ionized helium fraction,
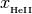 =
=  /
/ 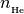
He3 (array): doubly ionized helium fraction,
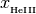 =
=  /
/ 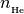
Teq (array): equilibrium temperature
cool (array): cooling rate at final state (should be equal to heat)
heat (array): heating rate at final state (should be equal to cool)
itr (int): number of iterations to converge
Tcmb (float): CMB temperature at input redshift
Notes:
This class finds solutions (H1, H2, He1, He2, He3, Teq) to the following equations
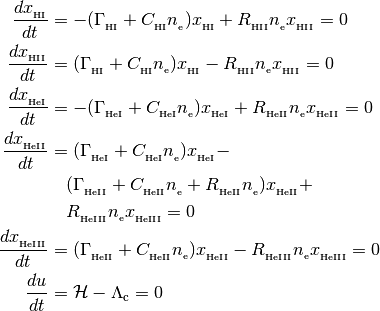
with the following closure relationships
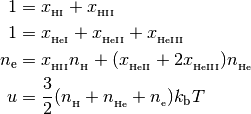
In the equations above, the
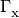 are photoionization
rates, the
are photoionization
rates, the 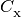 are collisional ionization rates, the
are collisional ionization rates, the
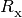 are recombination rates,
are recombination rates, 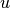 is the internal
energy,
is the internal
energy, 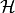 is the heating function, and
is the heating function, and
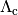 is the cooling function. These solutions depend
on temperature and density.
is the cooling function. These solutions depend
on temperature and density.Examples:
The following code will solve for photo-collisional-thermal ionization equilibrium at 128 densities using case B recombination rates for all species. The photoionization and heating rates are taken from the Haardt and Madau 2012 model. Note that the photoionization rate arrays are grouped with the chemistry rates and the photoheating rate arrays are grouped with the cooling rates:
import numpy as np import rabacus as ra N = 128; Yp = 0.24; z=3.0 fcA_H2 = 0.0; fcA_He2 = 0.0; fcA_He3 = 0.0 nH = 10**np.linspace( -4.0, -3.0, N ) / ra.U.cm**3 nHe = nH * 0.25 * Yp / (1-Yp) T = 10**np.linspace( 4.0, 5.0, N ) * ra.U.K hmr = ra.uv_bgnd.HM12_Photorates_Table() H1i = np.ones(N) * hmr.H1i(z) He1i = np.ones(N) * hmr.He1i(z) He2i = np.ones(N) * hmr.He2i(z) kchem = ra.f2py.ChemistryRates( T, fcA_H2, fcA_He2, fcA_He3, H1i=H1i, He1i=He1i, He2i=He2i ) H1h = np.ones(N) * hmr.H1h(z) He1h = np.ones(N) * hmr.He1h(z) He2h = np.ones(N) * hmr.He2h(z) kcool = ra.f2py.CoolingRates( T, fcA_H2, fcA_He2, fcA_He3, H1h=H1h, He1h=He1h, He2h=He2h ) x = ra.f2py.Solve_PCTE( nH, nHe, kchem, kcool, z )
rabacus.f2py.setup module¶
A python script that sets up the f2py shared object (fc.so).
rabacus.f2py.slab_base module¶
Slab geometry base class.
rabacus.f2py.slab_bgnd module¶
Wrapper to make python calling easy.
-
class
rabacus.f2py.slab_bgnd.Slab2Bgnd(Edges, T, nH, nHe, rad_src, rec_meth='fixed', fixed_fcA=1.0, atomic_fit_name='hg97', find_Teq=False, z=None, Hz=None, verbose=False, tol=0.0001, thin=False)[source]¶ Bases:
rabacus.f2py.slab_base.SlabBaseSolves a slab geometry in a uniform background. Radiation is implicitly incident from both sides of the slab. The slab is divided into Nl layers.
- Args:
Edges (array): Distance to layer edges
T (array): Temperature in each layer
nH (array): hydrogen number density in each layer
nHe (array): helium number density in each layer
rad_src (
BackgroundSource): Background source
Note
The arrays T, nH, and nHe must all be the same size. This size determines the number of shells, Nl. Edges determines the positions of the layer edges and must have Nl+1 entries.
Kwargs:
rec_meth (string): How to treat recombinations {“fixed”, “ray”}
fixed_fcA (float): If rec_meth = “fixed”, constant caseA fraction
atomic_fit_name (string): Source for atomic rate fits {“hg97”}
find_Teq (bool): If
False, use fixed input T, ifTruesolve for equilibrium Tz (float): Redshift, only need if find_Teq =
TrueHz (float): Hubble parameter at z if Hubble cooling is desired.
verbose (bool): Verbose output?
tol (float): tolerance for all convergence tests
thin (bool): if
Trueonly solves optically thinAttributes:
U (
Units)z_c (array): distance from surface of slab to center of layer
dz (array): thickness of layer
NH_c (array): H column density from surface of slab to center of layer
dNH (array): H column density through layer
NH1_c (array): HI column density from surface of slab to center of layer
dNH1 (array): HI column density through layer
H1i (array): HI photo-ionization rate
H1h (array): HI photo-heating rate
xH1 (array): H neutral fraction nHI / nH
xH2 (array): H ionized fraction nHII / nH
ne (array): electron number density
fcA_H2 (array): HII case A fraction
cool (array): cooling rate [erg / (cm^3 K)]
heat (array): heating rate [erg / (cm^3 K)]
heatH1 (array): contribution to heat from H1 photoheating
dtauH1_th (array): HI optical depth at H1 ionizing threshold through layer
tauH1_th_lo (array): HI optical depth below this layer
tauH1_th_hi (array): HI optical depth above this layer
NH1_thru (float): HI column density through entire slab
Nl (int): Number of layers
itr (int): Number of iterations to converge
Note
For many of the attributes above, there are analagous versions for helium. We also note that the source of the atomic rates fit is stored in the variable atomic_fit_name, but the source of the photoionization cross section fits are stored in the point source object in the variable px_fit_type.
-
write_to_file(fname, top_group='/', write_layers=True, write_centrals=True, write_averages=True, write_source=True)[source]¶ Writes a background slab out to an hdf5 file.
-
write_to_file_generic(fname, top_group, grp_name, obj, write_temperature=True, write_number_density=True, write_ionization_fractions=True, write_photoion_rates=True, write_photoheat_rates=True, write_mu=True)[source]¶ writes a lot of attributes to file fname in hdf5 group,
fname/top_group/grp_namethe attributes are taken from obj.
rabacus.f2py.slab_plane module¶
Wrapper to make the fortran calling identical to the python calling.
-
class
rabacus.f2py.slab_plane.SlabPln(Edges, T, nH, nHe, rad_src, rec_meth='fixed', fixed_fcA=1.0, atomic_fit_name='hg97', find_Teq=False, z=None, Hz=None, verbose=False, tol=0.0001, thin=False)[source]¶ Bases:
rabacus.f2py.slab_base.SlabBaseSolves a slab geometry with plane parallel radiation incident from one side. The slab is divided into Nl layers.
- Args:
Edges (array): Distance to layer edges
T (array): Temperature in each layer
nH (array): hydrogen number density in each layer
nHe (array): helium number density in each layer
rad_src (
PlaneSource): Plane source
Note
The arrays T, nH, and nHe must all be the same size. This size determines the number of shells, Nl. Edges determines the positions of the layer edges and must have Nl+1 entries.
Kwargs:
rec_meth (string): How to treat recombinations {“fixed”, “ray”}
fixed_fcA (float): If rec_meth = “fixed”, constant caseA fraction
atomic_fit_name (string): Source for atomic rate fits {“hg97”, “enzo13”}
find_Teq (bool): If
False, use fixed input T, ifTruesolve for equilibrium Tz (float): Redshift, only need if find_Teq =
TrueHz (float): Hubble parameter at z if Hubble cooling is desired.
verbose (bool): Verbose output?
tol (float): tolerance for all convergence tests
thin (bool): if
Trueonly solves optically thinAttributes:
U (
Units)z_c (array): distance from C to center of layer
dz (array): radial thickness of layer
NH_c (array): H column density from C to center of layer
dNH (array): H column density through layer
NH1_c (array): HI column density from C to center of layer
dNH1 (array): HI column density through layer
H1i (array): HI photo-ionization rate
H1h (array): HI photo-heating rate
xH1 (array): H neutral fraction nHI / nH
xH2 (array): H ionized fraction nHII / nH
ne (array): electron number density
fcA_H2 (array): HII case A fraction
cool (array): cooling rate [erg / (cm^3 K)]
heat (array): heating rate [erg / (cm^3 K)]
heatH1 (array): contribution to heat from H1 photo-heating
dtauH1_th (array): HI optical depth at H1 ionizing threshold through layer
tauH1_th_lo (array): HI optical depth below this layer
tauH1_th_hi (array): HI optical depth above this layer
NH1_thru (float): HI column density from C to R
Nl (int): Number of layers
itr (int): Number of iterations to converge
Note
For many of the attributes above, there are analagous versions for helium. We also note that the source of the atomic rates fit is stored in the variable atomic_fit_name, but the source of the photoionization cross section fits are stored in the point source object in the variable px_fit_type.
-
class
rabacus.f2py.slab_plane.Slab2Pln(Edges, T, nH, nHe, rad_src, rec_meth='fixed', fixed_fcA=1.0, atomic_fit_name='hg97', find_Teq=False, z=None, Hz=None, verbose=False, tol=0.0001, thin=False, i_rec_ems_prf=0)[source]¶ Bases:
rabacus.f2py.slab_base.SlabBaseSolves a slab geometry with plane parallel radiation incident from both sides. The slab is divided into Nl layers.
- Args:
Edges (array): Distance to layer edges
T (array): Temperature in each layer
nH (array): hydrogen number density in each layer
nHe (array): helium number density in each layer
rad_src (
PlaneSource): Plane source
Note
The arrays T, nH, and nHe must all be the same size. This size determines the number of shells, Nl. Edges determines the positions of the layer edges and must have Nl+1 entries.
Kwargs:
rec_meth (string): How to treat recombinations {“fixed”, “ray”}
fixed_fcA (float): If rec_meth = “fixed”, constant caseA fraction
atomic_fit_name (string): Source for atomic rate fits {“hg97”}
find_Teq (bool): If
False, use fixed input T, ifTruesolve for equilibrium Tz (float): Redshift, only need if find_Teq =
TrueHz (float): Hubble parameter at z if Hubble cooling is desired.
verbose (bool): Verbose output?
tol (float): tolerance for all convergence tests
thin (bool): if
Trueonly solves optically thini_rec_ems_prf (int): if
0recombination radiation is emitted isotropically (i.e. more attenuation), if1recombination radiation is emitted perpendicular to the layers.Attributes:
U (
Units)z_c (array): distance from surface of slab to center of layer
dz (array): thickness of layer
NH_c (array): H column density from surface of slab to center of layer
dNH (array): H column density through layer
NH1_c (array): HI column density from surface of slab to center of layer
dNH1 (array): HI column density through layer
H1i (array): HI photo-ionization rate
H1h (array): HI photo-heating rate
xH1 (array): H neutral fraction nHI / nH
xH2 (array): H ionized fraction nHII / nH
ne (array): electron number density
fcA_H2 (array): HII case A fraction
cool (array): cooling rate [erg / (cm^3 K)]
heat (array): heating rate [erg / (cm^3 K)]
heatH1 (array): contribution to heat from H1 photoheating
dtauH1_th (array): HI optical depth at H1 ionizing threshold through layer
tauH1_th_lo (array): HI optical depth below this layer
tauH1_th_hi (array): HI optical depth above this layer
NH1_thru (float): HI column density through entire slab
Nl (int): Number of layers
itr (int): Number of iterations to converge
Note
For many of the attributes above, there are analagous versions for helium. We also note that the source of the atomic rates fit is stored in the variable atomic_fit_name, but the source of the photoionization cross section fits are stored in the point source object in the variable px_fit_type.
rabacus.f2py.special_functions module¶
Wrapper to special function fortran module.
rabacus.f2py.sphere_base module¶
Sphere geometry base class.
rabacus.f2py.sphere_bgnd module¶
Solves a sphere immersed in a uniform background.
-
class
rabacus.f2py.sphere_bgnd.SphereBgnd(Edges, T, nH, nHe, rad_src, rec_meth='fixed', fixed_fcA=1.0, atomic_fit_name='hg97', find_Teq=False, z=None, Hz=None, em_H1_fac=1.0, em_He1_fac=1.0, em_He2_fac=1.0, verbose=False, tol=0.0001, thin=False, Nmu=32)[source]¶ Bases:
rabacus.f2py.sphere_base.SphereBaseStores and calculates equilibrium ionization (and optionally temperature) structure in a spherically symmetric geometry immersed in a uniform background. The sphere is divided into Nl shells. We will refer to the center of the sphere as “C” and the radius of the sphere as “R”.
Args:
Edges (array): Radius of all shell edges
T (array): Temperature in each shell
nH (array): Hydrogen number density in each shell
nHe (array): Helium number density in each shell
rad_src (
BackgroundSource): Background sourceNote
The arrays T, nH, and nHe must all be the same size. This size determines the number of shells, Nl. Edges determines the positions of the shell edges and must have Nl+1 entries.
Kwargs:
rec_meth (string): How to treat recombinations {“fixed”, “outward”, “radial”, “isotropic”}
fixed_fcA (float): If rec_meth = “fixed”, constant caseA fraction
atomic_fit_name (string): Source for atomic rate fits {“hg97”}
find_Teq (bool): If
False, use fixed input T, ifTruesolve for equilibrium Tz (float): Redshift, only need if find_Teq =
TrueHz (float): Hubble parameter at z if Hubble cooling is desired.
em_H1_fac (float): multiplicative factor for H1 recomb emission
em_He1_fac (float): multiplicative factor for He1 recomb emission
em_He2_fac (float): multiplicative factor for He2 recomb emission
verbose (bool): Verbose output?
tol (float): tolerance for all convergence tests
thin (bool): if
Trueonly solves optically thinNmu (int): number of polar angle bins
Attributes:
U (
rabacus.constants.units.Units)r_c (array): distance from C to center of shell
dr (array): radial thickness of shell
NH_c (array): H column density from C to center of shell
dNH (array): H column density through shell
NH1_c (array): HI column density from C to center of shell
dNH1 (array): HI column density through shell
H1i (array): HI photo-ionization rate
H1h (array): HI photo-heating rate
xH1 (array): H neutral fraction nHI / nH
xH2 (array): H ionized fraction nHII / nH
ne (array): electron number density
fcA_H2 (array): HII case A fraction
cool (array): cooling rate [erg / (cm^3 K)]
heat (array): heating rate [erg / (cm^3 K)]
heatH1 (array): contribution to heat from H1 photo-heating
dtauH1_th (array): HI optical depth at H1 ionizing threshold through shell
tauH1_th_lo (array): HI optical depth below this shell
tauH1_th_hi (array): HI optical depth above this shell
NH1_thru (float): HI column density from C to R
Nl (int): Number of shells
itr (int): Number of iterations to converge
Note
For many of the attributes above, there are analagous versions for helium. We also note that the source of the atomic rates fit is stored in the variable atomic_fit_name, but the source of the photoionization cross section fits are stored in the point source object in the variable px_fit_type.
rabacus.f2py.sphere_stromgren module¶
Solves a sphere with a point source at the center. Canonical examples are Tests 1 and 2 from http://arxiv.org/abs/astro-ph/0603199.
-
class
rabacus.f2py.sphere_stromgren.SphereStromgren(Edges, T, nH, nHe, rad_src, rec_meth='fixed', fixed_fcA=1.0, atomic_fit_name='hg97', find_Teq=False, z=None, Hz=None, em_H1_fac=1.0, em_He1_fac=1.0, em_He2_fac=1.0, verbose=False, tol=0.0001, thin=False, Nmu=32)[source]¶ Bases:
rabacus.f2py.sphere_base.SphereBaseStores and calculates equilibrium ionization (and optionally temperature) structure in a spherically symmetric geometry with a point source at the center. The sphere is divided into Nl shells. We will refer to the center of the sphere as “C” and the radius of the sphere as “R”.
Args:
Edges (array): Radius of all shell edges
T (array): Temperature in each shell
nH (array): Hydrogen number density in each shell
nHe (array): Helium number density in each shell
rad_src (
PointSource): Point sourceNote
The arrays T, nH, and nHe must all be the same size. This size determines the number of layers, Nl. Edges determines the positions of the shells that bound the layers and must have Nl+1 entries.
Kwargs:
rec_meth (string): How to treat recombinations {“fixed”, “outward”, “radial”, “isotropic”}
fixed_fcA (float): If rec_meth = “fixed”, constant caseA fraction
atomic_fit_name (string): Source for atomic rate fits {“hg97”}
find_Teq (bool): If
False, use fixed input T, ifTruesolve for equilibrium Tz (float): Redshift, only need if find_Teq =
TrueHz (float): Hubble parameter at z if Hubble cooling is desired.
em_H1_fac (float): multiplicative factor for H1 recomb emission
em_He1_fac (float): multiplicative factor for He1 recomb emission
em_He2_fac (float): multiplicative factor for He2 recomb emission
verbose (bool): Verbose output?
tol (float): tolerance for all convergence tests
thin (bool): if
Trueonly solves optically thinNmu (int): number of polar angle bins
Attributes:
U (
rabacus.constants.units.Units)r_c (array): distance from C to center of shell
dr (array): radial thickness of shell
NH_c (array): H column density from C to center of shell
dNH (array): H column density through shell
NH1_c (array): HI column density from C to center of shell
dNH1 (array): HI column density through shell
H1i (array): HI photo-ionization rate
H1h (array): HI photo-heating rate
xH1 (array): H neutral fraction nHI / nH
xH2 (array): H ionized fraction nHII / nH
ne (array): electron number density
fcA_H2 (array): HII case A fraction
cool (array): cooling rate [erg / (cm^3 K)]
heat (array): heating rate [erg / (cm^3 K)]
heatH1 (array): contribution to heat from H1 photo-heating
dtauH1_th (array): HI optical depth at H1 ionizing threshold through shell
tauH1_th_lo (array): HI optical depth below this shell
tauH1_th_hi (array): HI optical depth above this shell
NH1_thru (float): HI column density from C to R
Nl (int): Number of shells
itr (int): Number of iterations to converge
Note
For many of the attributes above, there are analagous versions for helium. We also note that the source of the atomic rates fit is stored in the variable atomic_fit_name, but the source of the photoionization cross section fits are stored in the point source object in the variable px_fit_type.