Single Zone Solvers¶
The single zone solvers calculate ionization and/or temperature equilibrium in situations where the densities and temperature can be characterized by single values. Three classes are used to handle three types of equilibrium,
Solve_CE:- Collisional Ionization Equilibrium. Finds ionization fractions at a fixed temperature such that collisional ionizations balance recombinations.
Solve_PCE:- Photo Collisional Ionization Equilibrium. Finds ionization fractions at a fixed temperature such that photo and collisional ionizations balance recombinations.
Solve_PCTE:- Photo Collisional Thermal Equilibrium. Finds ionization fractions and temperatures such that photo and collisional ionizations balance recombinations and heating balances cooling.
More preceisely, the single zone solvers find ionization fractions and/or temperatures that satisfy the following set of equations,
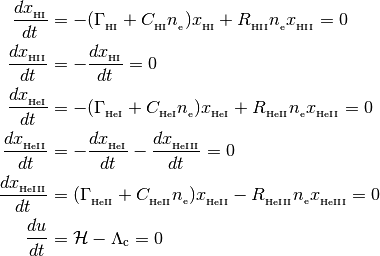
with the following closure relationships
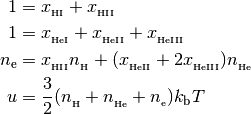
In the equations above, the 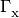 are photoionization
rates, the
are photoionization
rates, the 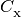 are collisional ionization rates, the
are collisional ionization rates, the
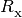 are recombination rates,
are recombination rates, 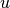 is the internal
energy,
is the internal
energy, 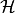 is the heating function, and
is the heating function, and
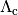 is the cooling function.
is the cooling function.
Collisional Ionization Equilibrium¶
The Solve_CE class assumes a fixed
temperature and that all photoionization rates are zero.
In this case, there is an analytic solution to the above
equations which depends only on the collisional ionization and recombination
rates at a given temperature. The following example will produce a solution
for 4 temperatures and will use case A rates for each solution (although
the case A fraction arguments can also be arrays).
import numpy as np
import rabacus as ra
N = 4
T = 10**np.linspace( 4.0, 5.0, N ) * ra.u.K
fcA_H2 = 1.0; fcA_He2 = 1.0; fcA_He3 = 1.0
kchem = ra.ChemistryRates( T, fcA_H2, fcA_He2, fcA_He3 )
x_ce = ra.Solve_CE( kchem )
The object x_ce now contains ionization fractions for neutral and
ionized hydrogen at the four input temperatures,
print x_ce.H1
[ 9.97918208e-01 3.73423460e-02 2.86333499e-04 1.71296398e-05] dimensionless
print x_ce.H2
[ 0.00208179 0.96265765 0.99971367 0.99998287] dimensionless
and ionization fractions for neutral, singly ionized, and doubly ionized helium at the same temperatures,
print x_ce.He1
[ 9.99999998e-01 9.78969652e-01 1.44418832e-02 1.60194516e-04] dimensionless
print x_ce.He2
[ 1.77227599e-09 2.10303478e-02 9.83482722e-01 1.13874960e-01] dimensionless
print x_ce.He3
[ 1.84382466e-34 2.68487133e-12 2.07539496e-03 8.85964845e-01] dimensionless
Photo Collisional Ionization Equilibrium¶
The Solve_PCE class assumes that the
temperature is fixed but includes non-zero photoionization rates.
These solutions depend on the density of hydrogen and helium as well
as temperature. In order to make the solvers aware of photoionization rates
they need to be included as arguments in the chemistry rates object. The
following example will get photoionization rates from the Haardt and Madau
2012 model and use them to solve for photo collisional equilibrium at
4 density-temperature pairs using case B recombination rates.
import numpy as np
import rabacus as ra
N = 4
Yp = 0.24
nH = np.ones(N) * 1.0e-3 / ra.u.cm**3
nHe = nH * 0.25 * Yp / (1-Yp)
pt = ra.HM12_Photorates_Table()
z = 3.0
H1i = np.ones(N) * pt.H1i(z)
He1i = np.ones(N) * pt.He1i(z)
He2i = np.ones(N) * pt.He2i(z)
T = 10**np.linspace( 4.0, 5.0, N ) * ra.u.K
fcA_H2 = 0.0; fcA_He2 = 0.0; fcA_He3 = 0.0
kchem = ra.ChemistryRates( T, fcA_H2, fcA_He2, fcA_He3,
H1i=H1i, He1i=He1i, He2i=He2i )
x_pce = ra.Solve_PCE( nH, nHe, kchem )
In the above example we have made the densities and photoionization
rates equal for all four temperatures, but this is not necessary
(i.e. each element of those arrays can have a different value). The
object x_pce now contains ionization fractions for neutral and
ionized hydrogen at the four input temperatures,
print x_pce.H1
[ 3.54508432e-04 1.82664733e-04 5.51303759e-05 6.31418283e-06] dimensionless
print x_pce.H2
[ 0.99964549 0.99981734 0.99994487 0.99999369] dimensionless
and ionization fractions for neutral, singly ionized, and doubly ionized helium at the same temperatures,
print x_pce.He1
[ 1.99727141e-04 7.38265776e-05 2.63511233e-05 2.42439604e-05] dimensionless
print x_pce.He2
[ 0.32318511 0.21074971 0.12540601 0.03435841] dimensionless
print x_pce.He3
[ 0.67661516 0.78917647 0.87456764 0.96561735] dimensionless
Photo Collisional Thermal Equilibrium¶
The Solve_PCTE class finds a
temperatures and ionization fractions that satisfy the above equations
for an array of densities.
Because inverse Compton scattering off of CMB photons can be an appreciable
cooling mechanism, this class takes a redshift as one of its arguments.
The following example will get photoionization and photoheating rates from
the Haardt and Madau 2012 model and use them to solve for photo collisional
thermal equilibrium at 4 densities.
Note that the photoheating rates are attached to the cooling object just
as the photoionization rates are attached to the chemistry object.
Also note that temperatures are used to initialize the chemistry and cooling
objects, but these temperatures will be changed to the equilibrium
temperatures during the call to the solver.
import numpy as np
import rabacus as ra
N = 4
Yp = 0.24
nH = 10**np.linspace( -5.0, -1.0, N ) / ra.u.cm**3
nHe = nH * 0.25 * Yp / (1-Yp)
pt = ra.HM12_Photorates_Table()
z = 3.0
H1i = np.ones(N) * pt.H1i(z)
He1i = np.ones(N) * pt.He1i(z)
He2i = np.ones(N) * pt.He2i(z)
H1h = np.ones(N) * pt.H1h(z)
He1h = np.ones(N) * pt.He1h(z)
He2h = np.ones(N) * pt.He2h(z)
T = 10**np.linspace( 4.0, 5.0, N ) * ra.u.K
fcA_H2 = 0.0; fcA_He2 = 0.0; fcA_He3 = 0.0
kchem = ra.ChemistryRates( T, fcA_H2, fcA_He2, fcA_He3,
H1i=H1i, He1i=He1i, He2i=He2i )
kcool = ra.CoolingRates( T, fcA_H2, fcA_He2, fcA_He3,
H1h=H1h, He1h=He1h, He2h=He2h )
x_pcte = ra.Solve_PCTE( nH, nHe, kchem, kcool, z )
Note
Hubble cooling can be included by passing in the hubble parameter at the desired redshift using the keyword argument Hz. For example
Hz = ra.planck13_cosmology.Hz(z)
x_pcte = ra.Solve_PCTE( nH, nHe, kchem, kcool, z, Hz=Hz )
We have used non-uniform values for both the density and
temperature arrays in this example. The particular temperatures used
to instantiate the chemistry and cooling objects is not important as
this solver will converge to the equilibrium temperatures for the
given densities. The returned object x_pcte contains ionization
fractions and equilibrium temperatures for the input densities. The
ionization fractions for neutral and ionized hydrogen are,
print x_pcte.H1
[ 2.19371954e-06 2.40811392e-05 8.76128859e-04 2.65644453e-02] dimensionless
print x_pcte.H2
[ 0.99999781 0.99997592 0.99912387 0.97343555] dimensionless
The ionization fractions for neutral, singly ionized, and doubly ionized helium are,
print x_pcte.He1
[ 1.26614727e-08 1.94244006e-06 9.45705638e-04 4.52573115e-02] dimensionless
print x_pcte.He2
[ 0.00311191 0.03711927 0.56211876 0.93000539] dimensionless
print x_pcte.He3
[ 0.99688808 0.96287879 0.43693553 0.0247373 ] dimensionless
and the equilibrium temperatures at the input densities are,
print x_pcte.Teq
[ 17989.27445847 35889.65514996 19901.78191525 12452.52329718] K