Back to Guide

Surface tutorial

_images/surface.png

Example of a Surface formed by four triangles.

class pyny3d.geoms.Surface(polygons, holes=[], make_ccw=True, melt=False, check_contiguity=False, **kwargs)[source]

This class groups contiguous polygons (coplanars or not). These polygons cannot overlap each other on the z=0 projection*.

This object is a composition of polygons and holes. The polygons can be used to “hold up” other objects (points, other polygons...) and to compute shadows. The holes exist only to prevent the program to place objects on them. The shadows computation do not take care of the holes**, instead, they can be emulated by a collection of polygons.

Instances of this class work as iterable object. When indexed, returns the pyny.Polygons which conform it.

Parameters:
  • polygons (list of ndarray, list of pyny.Polygon) – Polygons to be set as Surface. This is the only necessary input to create a Surface.
  • holes (list of ndarray, list of pyny.Polygon) – Polygons to be set as holes of the Surface.
  • make_ccw (bool) – If True, points will be sorted ccw for each polygon.
  • melt (bool) – If True, the melt() method will be launched at initialization.
  • check_contiguity (bool) – If True, contiguous() will be launched at initialization.
Returns:

None

Note

* For models with planes stacked in column, use the Place class to distinct them. For example, a three-storey building structure can be modeled by using one pyny.Place for storey where the floor is a Surface and the columns are Polyhedra.

Note

** In the future versions of this library it will simulate shadows through the holes.

Non-trivial methods

Following the same structure than Polygon tutorial, the non-trivial methods will be explained and the trivial ones will be only listed. You can also use the Surface documentation.

Trivial methods:

method description
.get_area() Returns the real area
.get_height() Returns the z value for a list of points
.contiguous() Returns whether a set of polygons are contiguous
.add_holes() Add holes to the surface
.lock() Precomputes some values to speedup shading

The methods to transform the classes are explained in detail separately in Transformations.

The .classify() method is discussed separately in PiP and Classify tutorial.

intersect_with

Calculates the intersection between the polygons in the surface and an external polygon, in the z=0 projection.

This method fully rely on the shapely.Polygon.intersection() method. The way this method is used is intersecting this polygon recursively with all the identified polygons which overlaps with it in the z=0 projection.

The only thing that can be confusing is the output. It is a dictionary in which, the different intersections are classified with the index of the Surface’s polygon involved.

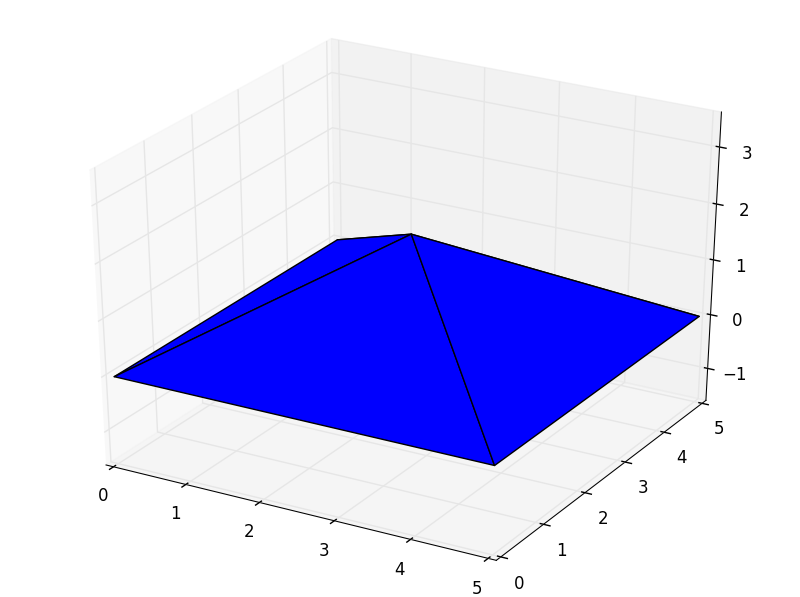
To illustrate it:

import numpy as np
import pyny3d.geoms as pyny

# Geometries (all in z=0)
surface = pyny.Surface([np.array([[0,0], [5,0], [2.5,2.5]]),
                        np.array([[5,0], [5,5], [2.5,2.5]]),
                        np.array([[5,5], [0,5], [2.5,2.5]]),
                        np.array([[0,5], [0,0], [2.5,2.5]])])
clip_polygon = pyny.Polygon(np.array([[1, 0], [4, 0], [2.5, 5]]))

# Intersection
inter_polys = surface.intersect_with(clip_polygon)

# Viz
## Creating a surface with the intersection polygons
inter_surf = pyny.Surface([pyny.Polygon(poly) for _, poly in inter_polys.items()])
surface.plot('b')
clip_polygon.plot('b')
inter_surf.plot('b')
_images/clip.png

Four coplanar and contiguous polygons, another polygon to clip with and the result of clipping

The inter_polys dictionary has four entries: the four polygons generated through the intersection referenced to the Surface.polygons.

In [1]: inter_polys
Out[1]: 
{0: array([[ 4.        ,  0.        ],
           [ 1.        ,  0.        ],
           [ 1.42857143,  1.42857143],
           [ 2.5       ,  2.5       ],
           [ 3.57142857,  1.42857143]]),
 1: array([[ 3.07692308,  3.07692308],
           [ 3.57142857,  1.42857143],
           [ 2.5       ,  2.5       ]]),
 2: array([[ 2.5       ,  5.        ],
           [ 3.07692308,  3.07692308],
           [ 2.5       ,  2.5       ],
           [ 1.92307692,  3.07692308]]),
 3: array([[ 1.42857143,  1.42857143],
           [ 1.92307692,  3.07692308],
           [ 2.5       ,  2.5       ]])}

contiguous and melt

.contiguous() checks whether a set of convex polygons are all contiguous and coplanar and melt() computes the union of these polygons if they give True in the first method. Two polygons are considered contiguous if they share, at least, two vertices.

The verification is not complete, it is simplified. For a given set of polygons this method will chechk if the number of common vertices among them equals or exceeds a certain number of common vertices. Anyway, this little algorithm will never declare a contiguous set of polygons as non-contiguous, but it can fail in the reverse for certain geometries where polygons have several common vertices among them.

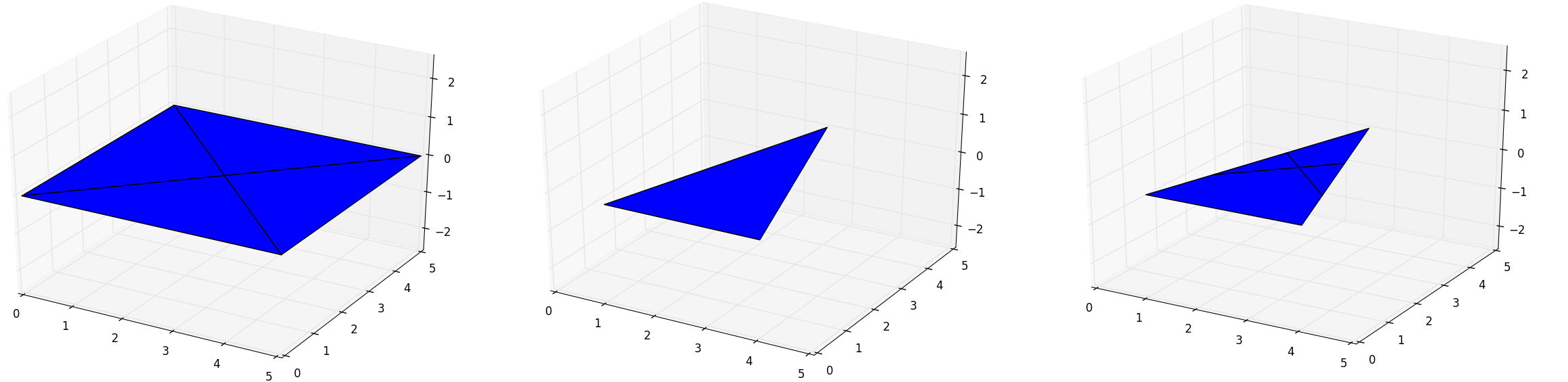
The next example is done for the previous set of polygons:

In [2]: import numpy as np
   ...: import pyny3d.geoms as pyny
   ...: 

In [3]: surface = pyny.Surface([np.array([[0,0], [5,0], [2.5,2.5]]),
   ...:                         np.array([[5,0], [5,5], [2.5,2.5]]),
   ...:                         np.array([[5,5], [0,5], [2.5,2.5]]),
   ...:                         np.array([[0,5], [0,0], [2.5,2.5]])])
   ...: 

In [4]: surface.plot('b')

In [5]: pyny.Surface.contiguous(surface.polygons)  # static method
Out[5]: True

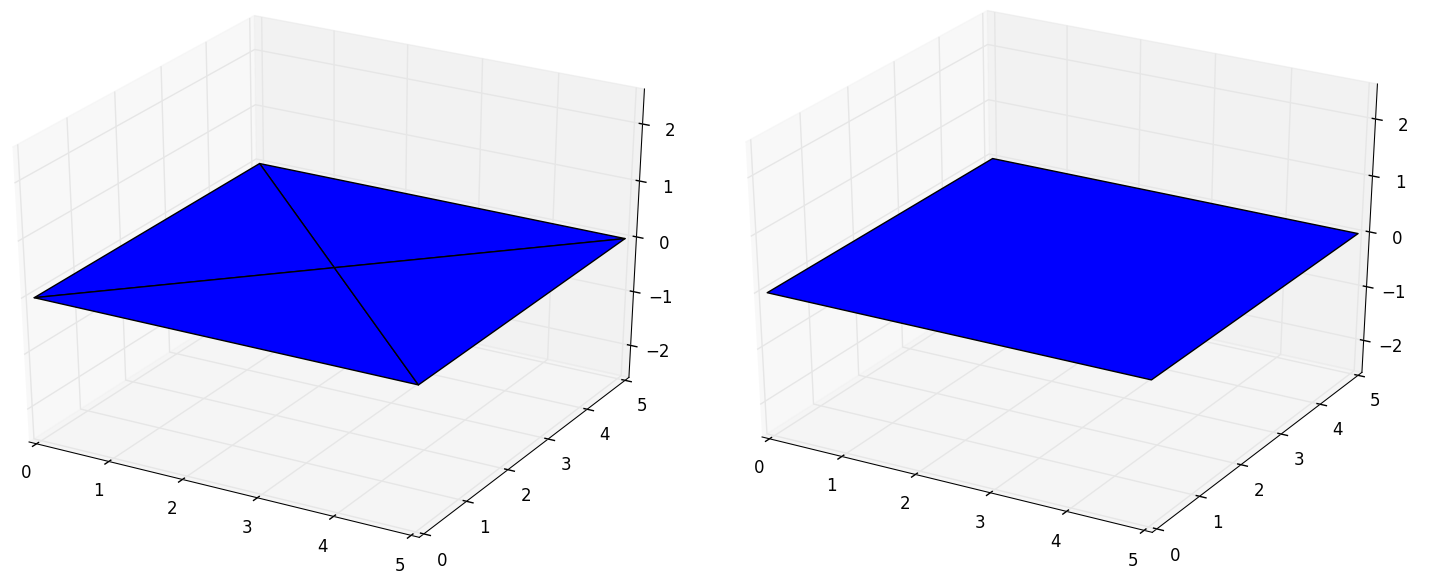
In [6]: surface.melt()
   ...: surface.plot('b')
   ...:
_images/melt1.png

Union of four coplanar and contiguous polygons

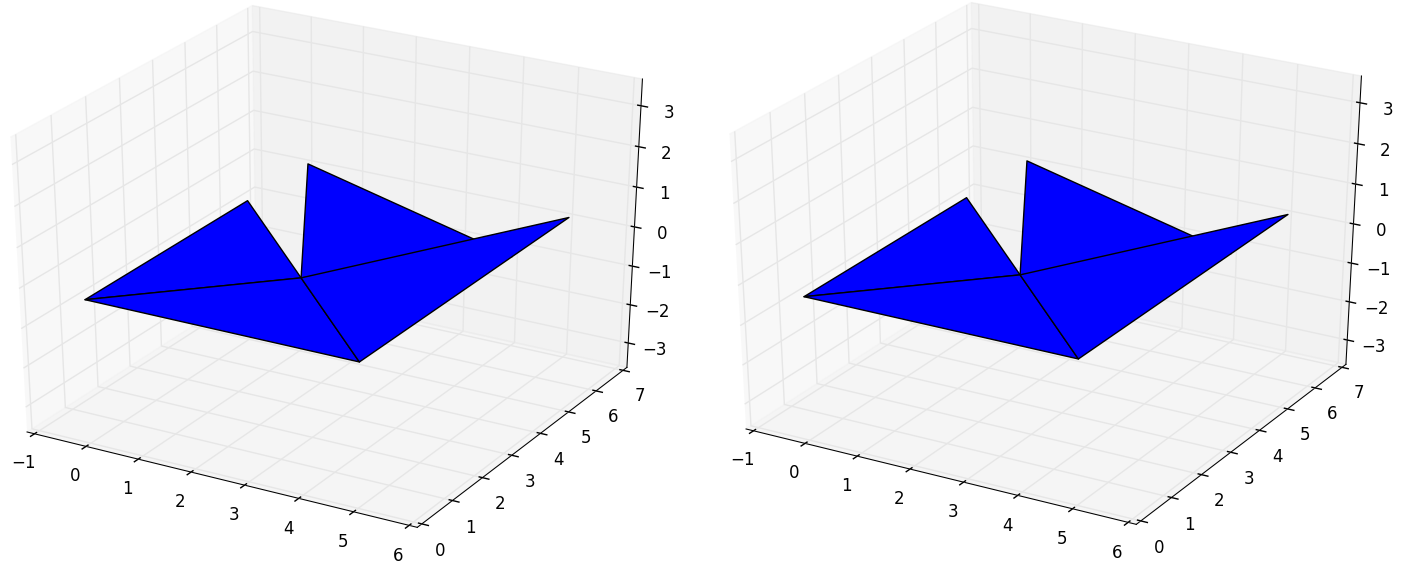
On the other hand, if the union is non-convex, although the polygons individually are, the method will compute the convex union anyway. This will happen when the number of non-coincident vertices are close to cero. In the next examples we are going to see how for one vertex we can make the method fail but we cannot for two.

In [7]: surface = pyny.Surface([np.array([[0,0], [5,0], [2.5,2.5]]),
   ...:                         np.array([[5,0], [5,5], [2.5,2.5]]),
   ...:                         np.array([[5,5], [0,7], [2.5,2.5]]),
   ...:                         np.array([[0,5], [0,0], [2.5,2.5]])])
   ...: 

In [8]: surface.plot('b')

In [9]: pyny.Surface.contiguous(surface.polygons)
Out[9]: True

In [10]: surface.melt()
   ....: surface.plot('b')
   ....:
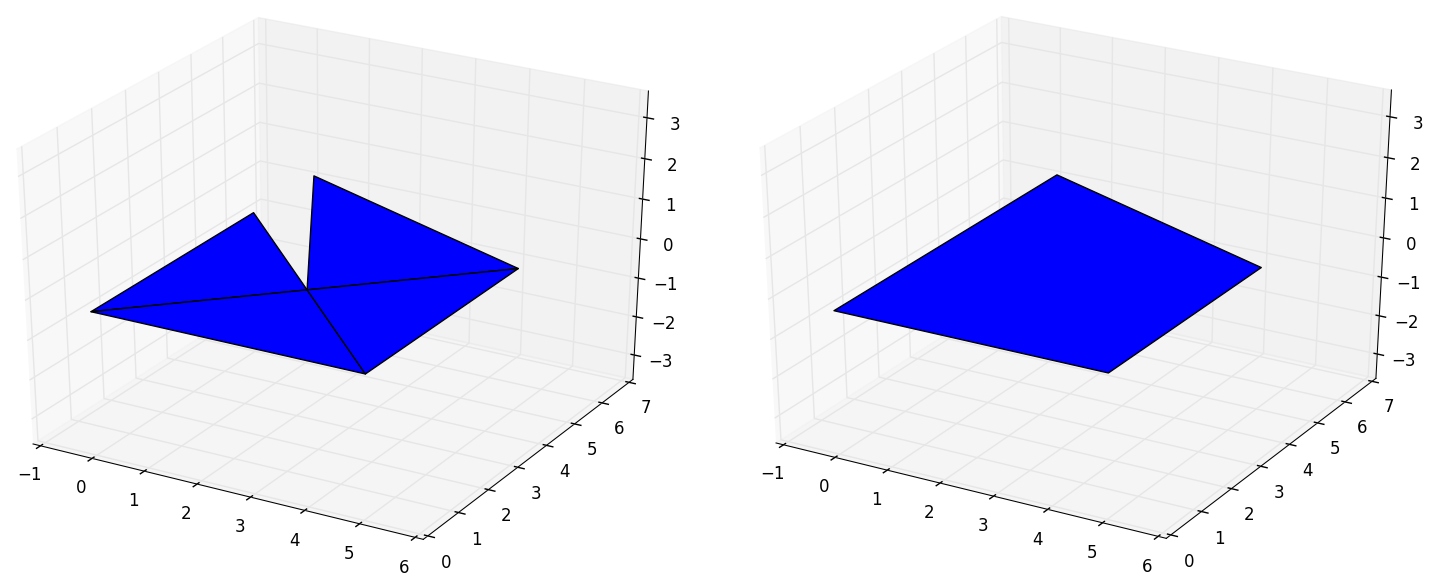
_images/melt2.png

Error at melting non-convex polygons with one non-coincident vertex

When the .melt() method cannot apply any union it lefts the Surface as it is:

In [11]: surface = pyny.Surface([np.array([[0,0], [5,0], [2.5,2.5]]),
   ....:                         np.array([[5,0], [5,7], [2.5,2.5]]),
   ....:                         np.array([[5,5], [0,7], [2.5,2.5]]),
   ....:                         np.array([[0,5], [0,0], [2.5,2.5]])])
   ....: 

In [12]: surface.plot('b')

In [13]: pyny.Surface.contiguous(surface.polygons)
Out[13]: False

In [14]: surface.melt()
   ....: surface.plot('b')
   ....:
_images/melt3.png

A Surface with two non-coincident vertices

Does this mean that .melt() method is unusable? Absolutely not. If the set of polygons are known to have a convex union the problem will not exist. And anyway, the method fails in very specific and known cases so you can control when and where use it. Furthermore, you can check the results visually.


Next tutorial: Polyhedron tutorial