Back to Guide
Transformations¶
pyny3d have some global methods to transform objects. These are .move(),
.rotate(), .mirror() and .matrix(). In this section we are
going to see some examples for all of them for the following geometry:
import numpy as np
import pyny3d.geoms as pyny
# Declaring the geometry
polygon = pyny.Polygon(np.array([[8,0], [15,0], [15,9], [8,9]]))
## Surface
poly_surf_0 = [np.array([[0,0,0], [7,0,0], [7,10,2], [0,10,2]]),
np.array([[0,10,2], [7,10,2], [3,15,3.5]]),
np.array([[0,10,2], [3,15,3.5], [0,15,3.5]]),
np.array([[7,10,2], [15,10,2], [15,15,3.5], [3,15,3.5]])]
## Obstacles
wall_1 = np.array([[0,0,4], [0.25,0,4], [0.25,15,4], [0,15,4]])
wall_2 = np.array([[0,14.7,5], [15,14.7,5], [15,15,5], [0,15,5]])
chimney = np.array([[4,0,7], [7,0,5], [7,3,5], [4,3,7]])
# Building the solution
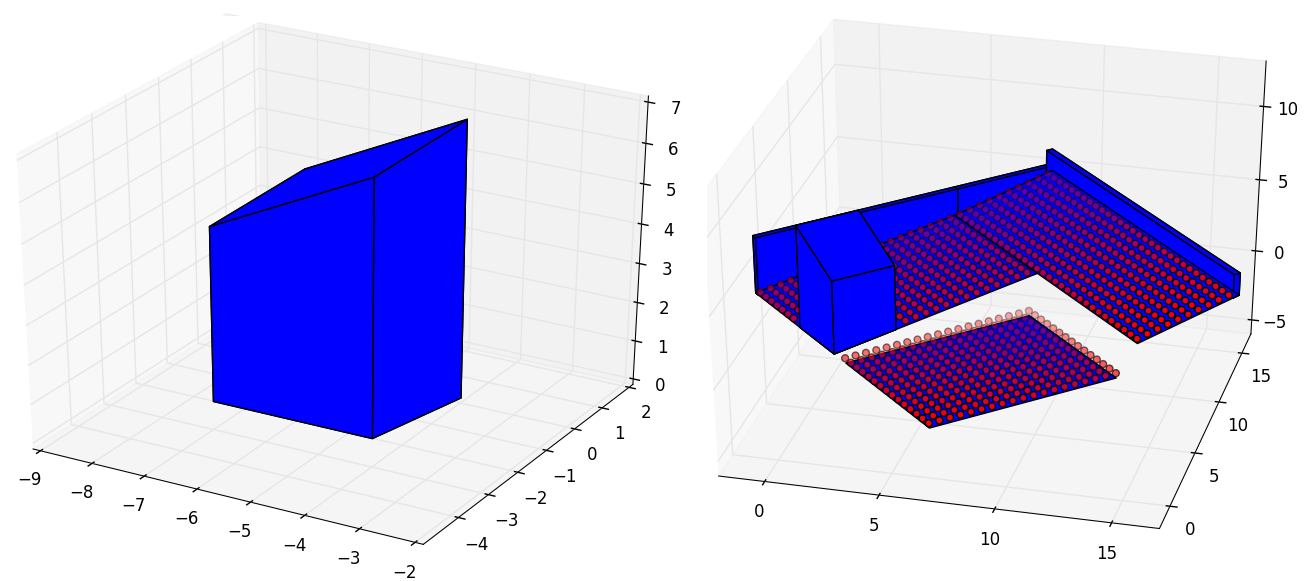
place_0 = pyny.Place(poly_surf_0, melt=True)
place_0.add_extruded_obstacles([wall_1, wall_2, chimney])
polyhedron = place_0.polyhedra[-1]
place_1 = pyny.Place(pyny.Surface(polygon))
space = pyny.Space([place_0, place_1])
space.mesh(0.5)
# Viz
space.iplot(c_poly='b')
It is important to note that in the case that the object we want to transform
is a Space, we have, except for .rotate(), the inplace option. Through
its activation we can tell the library to automatically add the transformed
form of the object to the current Space. That is, if we move an Space with
inplace=True we are actually duplicating it, because we are adding a new
Space to the original one. For the rest of classes this lacks of sense, because
they do not stack; instead, they will return independent instances or lists of
intances.
For example, it is completely normal to move a building and add the copy to the same Space of the original (creating a neibourhood) but it is incongruent to move a Polygon and add the new Polygon to the original one. A Polygon object only contains one Polygon.
move¶
This method is the simplest one. Indeed we will see how it works internally in the Space tutorial section. We only need to give the distance we want to displace in a tuple or ndarray:
In [1]: polygon_moved = polygon.move((100, 200, 300))
...: polygon_moved.plot('b')
...:
In [2]: space.save() # save the current state of the Space
...: space.move((-10, -10, 10), inplace=True)
...: space.iplot(c_poly='b', s_sop=10)
...: space = space.restore() # restore the Space to the state before the duplication
...:
rotate¶
It is possible to rotate all the elements in an object through a matrix operation that changes its the reference system. If the axis argument is left None (by default) the rotation will be done about the centroid.
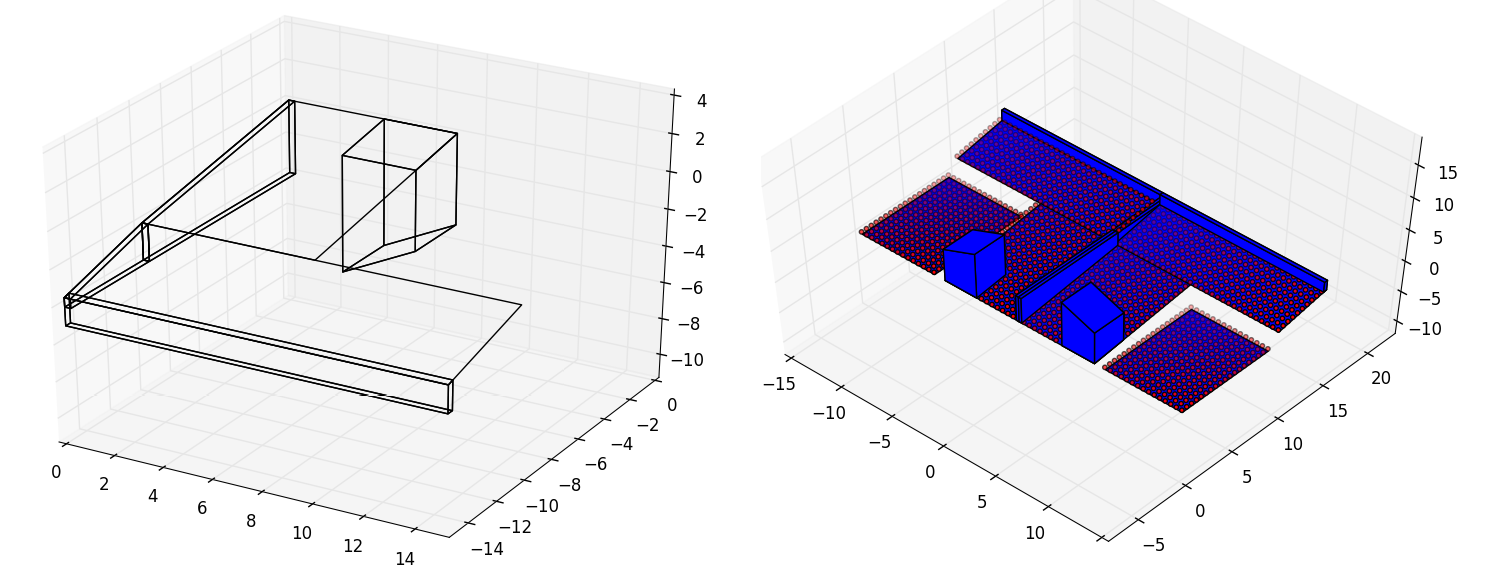
In [3]: polyhedron_rotated = polyhedron.rotate(np.pi)
...: polyhedron_rotated.plot('b')
...:
In [4]: space_rotated = space.rotate(-np.pi/4)
...: space_rotated.iplot(c_poly='b')
...:
Note
In the version 0.2, it is possible to rotate about axes aligned with x and y, not only with z.
mirror¶
Generates a symmetry of the Space respect global axes. If 'x' is inputed,
the symmetry will be done so that all the x coordinates will be -x. It
is also possible to do multiple symmetries at once by introducing, for
example 'xy'.
In [5]: place_symmetry = place_0.mirror('yz')
...: place_symmetry.plot('t') # better visualization in transparent
...:
In [6]: space.save()
...: space.mirror('x', inplace=True)
...: space.iplot(c_poly='b', s_sop=10)
...: space = space.restore()
...:
matrix¶
This function is actually the .move() method repeated for the main
directions. The first number of the tuple is the times that the object has to
be repeated and the second one is the distance between the same point for
the copies.
In order to improve the visualization I am going to add a Surface in z=0 that simulates the floor.
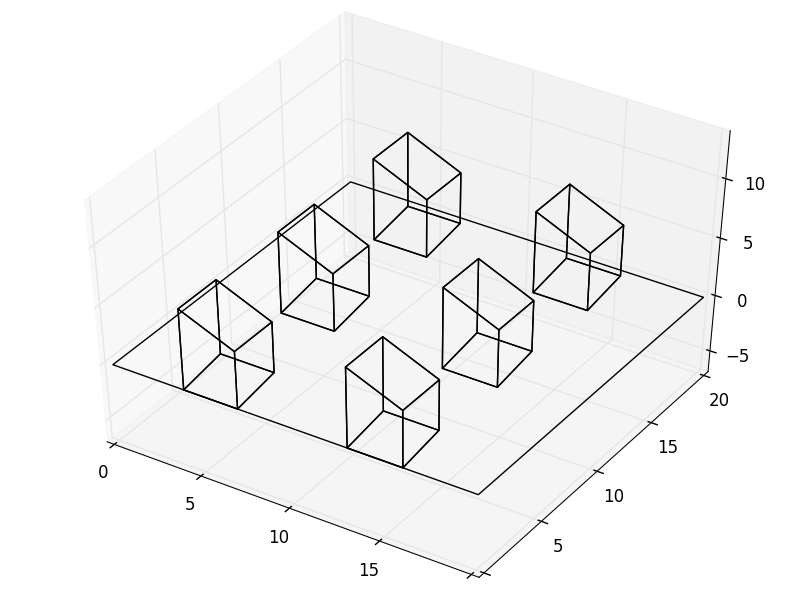
In [7]: polyhedra_list = polyhedron.matrix(x=(2, 9), y=(3, 8))
...: place = pyny.Place(surface=np.array([[0, 0], [20, 0], [20, 20], [0, 20]]),
...: polyhedra=polyhedra_list)
...: place.plot('t')
...:
Next tutorial: Polygon tutorial