Back to Guide
Basic shading tutorial¶
First of all: what does “shading” imply in pyny3d?:
The shading simulation is a process where a discrete data time series is assigned to a set of sensible points spreaded through a pyny.Space object accordingly to its geometric distribution and to the Sun positions.
What is really important to understand here is that it is a discrete operation. Discrete because the Sun positions are given by a finite number of data samples associated to (azimuth, zenit) pairs, and discrete because the shadows projections are not calculated over continuous surfaces, it is done independently for each point in the Space. In short:
For each sample, each point will be asked whether it is illuminated by the Sun or not.
Well, not exactly. If it were totally true the execution time would be very too expensive. What pyny3d does to shorten this process is to discretize the cartesian plane where the (azimuth, zenit) pairs lay. Thanks to this discretization (Voronoi) it is possible to reduce the Sun positions from several thousands to few hundreds without loosing too much information.
In view of the fact that there are, for example, more than 8000 sunny half-hour intervals in an year, the program precomputes a discretization for the Solar Horizont, (azimuth, zenit) pairs, and classify the time vector and the data into it. The goal is to approximate these 8000 static simulations to a less than 300 with an error of less than 3º (0.05rads). Of course, it is possible to select the fineness for the discretization process due to this affects the performance of the simulations.
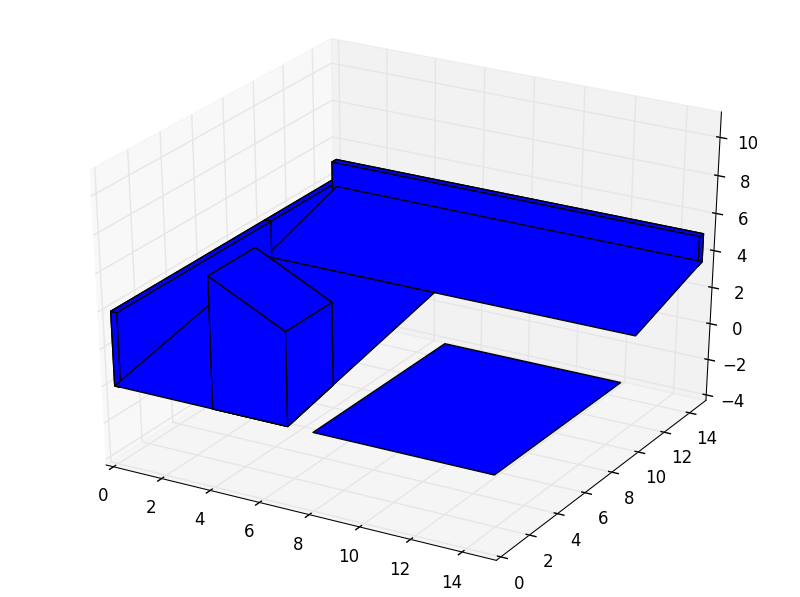
For this tutorial we are going to use the same geometry model that we have been using in previous tutorials but, in these case, we are not initialize it with points:
import numpy as np
import pyny3d.geoms as pyny
# Declaring the geometry
## Surface
poly_surf_0 = [np.array([[0,0,0], [7,0,0], [7,10,2], [0,10,2]]),
np.array([[0,10,2], [7,10,2], [3,15,3.5]]),
np.array([[0,10,2], [3,15,3.5], [0,15,3.5]]),
np.array([[7,10,2], [15,10,2], [15,15,3.5], [3,15,3.5]])]
poly_surf_1 = [np.array([[8,0,0], [15,0,0], [15,9,0], [8,9,0]])]
## Obstacles
wall_1 = np.array([[0,0,4], [0.25,0,4], [0.25,15,4], [0,15,4]])
wall_2 = np.array([[0,14.7,5], [15,14.7,5], [15,15,5], [0,15,5]])
chimney = np.array([[4,0,7], [7,0,5], [7,3,5], [4,3,7]])
# Building the solution
place_0 = pyny.Place(poly_surf_0, melt=True)
place_0.add_extruded_obstacles([wall_1, wall_2, chimney])
place_1 = pyny.Place(poly_surf_1)
space = pyny.Space([place_0, place_1])
# Viz
space.iplot(c_poly='b')
shadows module¶
This pyny3d’s module contains two classes to manage the shading simulations and its visualizations. Indeed, they are named ShadowsManager and Viz, respectively.
In general, performing shading simulations is quite simple but, in order to keep everything under control it is very important to know what the simualtor needs, and distinct what of their needs can be omitted. For this reason, we are going to start by the simplest usage of the classes mentioned:
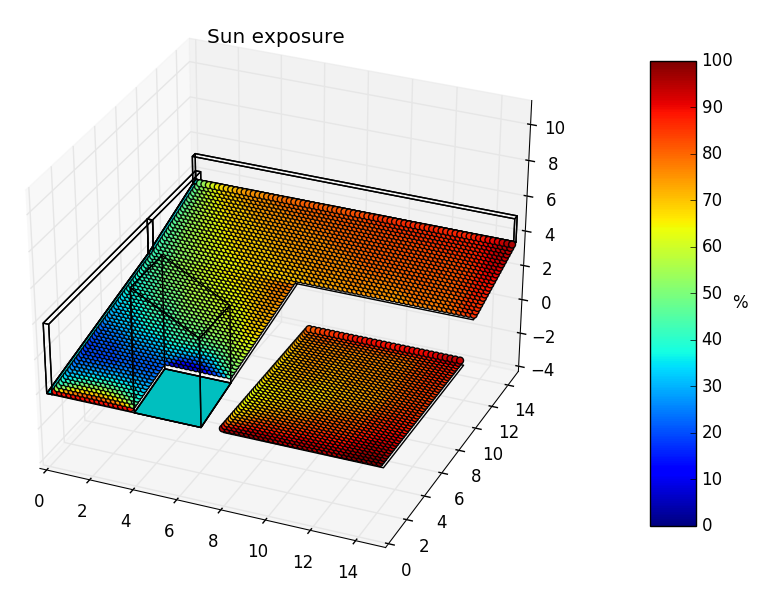
In [1]: S = space.shadows(init='auto', resolution='high') # Initializes a ShadowsManager object
In [2]: S
Out[2]: <pyny3d.shadows.ShadowsManager at 0xb0dfd37e48>
In [3]: S.viz.exposure_plot(c_poly='b') # Use ShadowsManager.Viz.<plot> for visualizations
As you are probably wondering, it is imposible to perform such calculation
without information like latitude or radiation time series. And You are right,
it is impossible. What init='auto' actually does is to fill automatically
all the simulation parameters with arbitrary information. For this reason, the
'auto' initialization should be used only as a verification that everything
goes as predicted.
ShadowsManager¶
The ShadowsManager (doc: ShadowsManager) can be initialize as
standalone object or associated to a pyny.Space through the .shadows()
method, which is the natural way.
For convenience, the time is managed in absolute minutes within the range of a year, that is, the first possible interval is the Jan 1 00:00 [0] and the last is Dec 31 23:59 [525599]. February 29 is not taken into account.
To compute a shading simulation over a pyny.Space, the following requeriments have to be satisfied:
The pyny.Space needs to have a set of points. Or, more specifically, at least one pyny.Place in the pyny.Space needs to have a set of points.
The following ShadowsManager attributes should be declared. They are easily recognizable because all of them have the ‘arg_’ prefix:
.arg_data
Data timeseries to project on the 3D model (radiation, for example). If None, by default, it will created a auxiliar data vector which fits with
.arg_tand it will be filled with ones.type: ndarray (shape=N), None
.arg_t
Time vector in absolute minutes or datetime objects. It needs to fit with
.arg_data.type: ndarray or list, None
.arg_dt
Interval time in minutes to generate t vector. If
.arg_tis None, it will be created as a regular interval time vector.type: int, None
.arg_latitude
Local latitude.
type: float (radians)
.arg_vor_size
For now, the Solar Horizont discretization is approached only with squared meshes (this will be changed in the future). The way to control the fineness of the mesh (the mesh size) is setting this attribute. By default, it is 0.15 radians (8.6 deg).
type: float (radians)
The rest of the arguments are optative. With them, we can ask for the real time in the computations (instead of solar time) or tune the simulation process itself:
.arg_run_true_time
If True, the simulation will return the solution in both solar and real time. In this case, it is required to set the next two attributes (
.arg_longitude,.arg_UTC). By default it is False.type: bool
.arg_longitude
Local longitude. Only used if
.arg_run_true_time = Truetype: float (radians)
.arg_UTC
Local UTC. Only used if
.arg_run_true_time = Truetype: int
.arg_zenitmin
Minimum zenit used in calculations. Due to trigonometric approximations when zenit tends to 0, it is safer to avoid values lower than a certain threshold. For low threshold values the affection to the results’ quality is irrelevant because the ignored intervals are very few and at sunrise and sunset, where the radiation is unsignificant relatively to the rest of the day. It is 0.1 radians (5.7 deg) by default.
type: float (radians)
init=’auto’¶
When we set the init parameter in space.shadows() as ‘auto’, what we
are technically declaring is: “I don’t care about the .arg_ parameters or
whether the Space has points declared or not, just fill them all as you want
and generate a sample simulation”. Obviously, you will not have a “true time”
solution this way.
However, this initialization will let you introduce the following parameters (but will not obligate):
- data
- t
- dt
- latitude
Even, it will respect the Space’s set of points, if it exists. Here we can see an example:
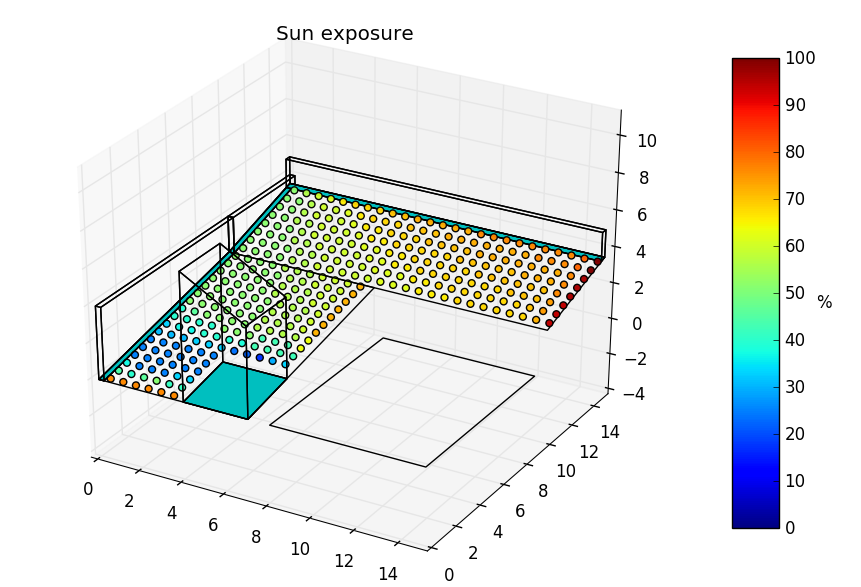
In [4]: space_copy = space.copy()
...: space_copy.clear_sets_of_points()
...: space_copy[0].mesh(0.6) # Points only in place #1
...:
In [5]: S = space_copy.shadows(init='auto', dt=120, latitude=0.001)
...: S.viz.exposure_plot()
...:
To make our life easier, we can adjust the simulations in 'auto' mode with
the resolution argument. This also affects the time vector generated and
the Voronoi’s diagram mesh size.
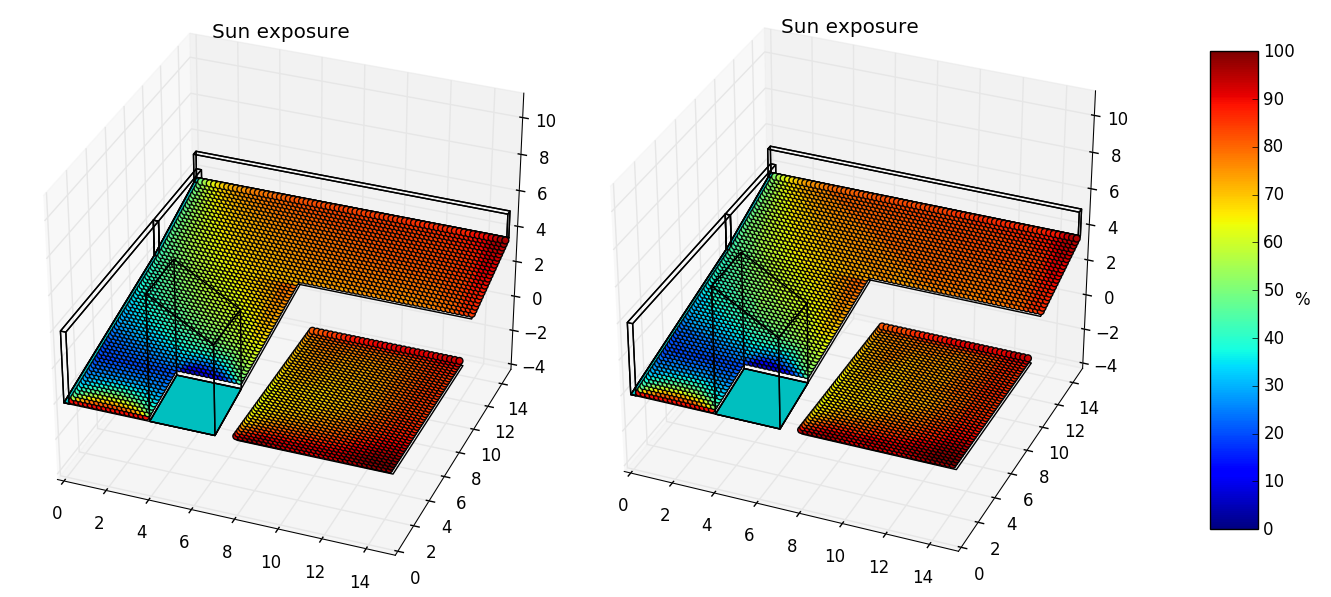
In [6]: space.clear_sets_of_points()
In [7]: space_copy = space.copy()
...: space_copy.shadows(init='auto', resolution='low').viz.exposure_plot()
...:
In [8]: space_copy = space.copy()
...: space_copy.shadows(init='auto', resolution='mid').viz.exposure_plot()
...:
In [9]: space_copy = space.copy()
...: space_copy.shadows(init='auto', resolution='high').viz.exposure_plot()
...:
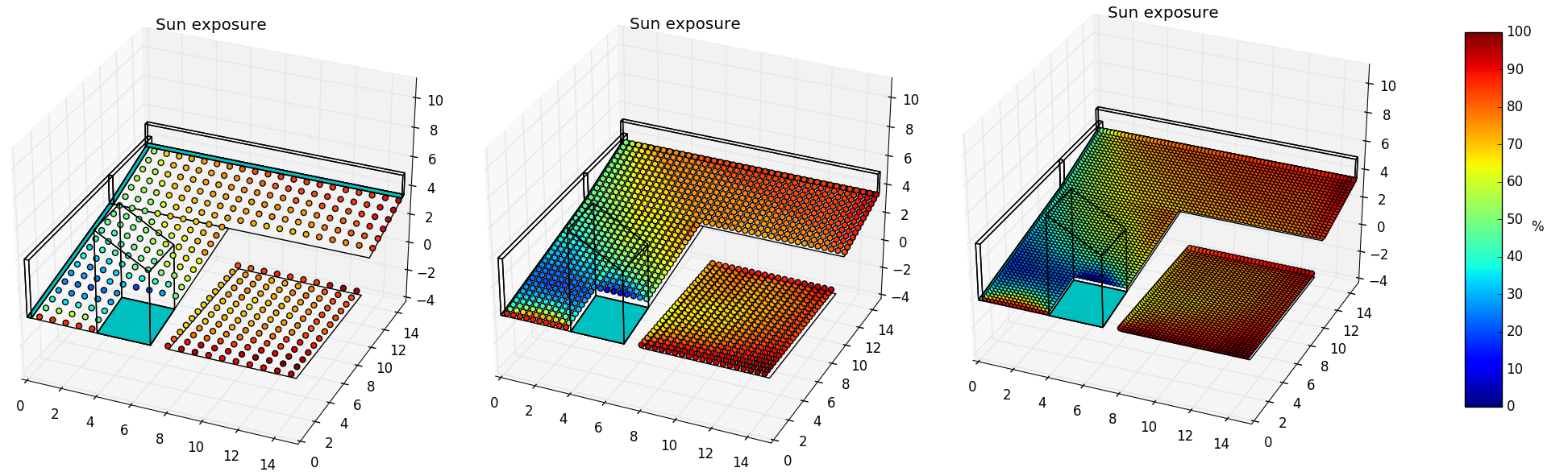
Visualization for the low, mid and high resolution. The execution time was 443 ms, 1.12 s and 3.58 s respectively.
Warning
The points generated through init=’auto’ are left attached to the Space after the simulation.
Warning
Simulations made in 'auto' mode are tuned to perform
relatively fast in order to get a rapid and smooth visualization. For this
reason, the t vector generated is considerably short and the Voronoi’s
diagram mesh size is excedingly small. If you are going to use real
information I strongly recommend you to do not use the 'auto'
initialization for the serious work.
The solution¶
pyny3d was created to work as a complement for larger applications. Until now, we have seen how to insert data, work with them and perform simulations. The next step is: “how and where is the simulation’s solution?”.
The answer is that it is a numpy array (surprise) that stores the ON/OFF state of each sensible point in each instant indicated in t. This array is in ShadowManager.light and its rows correspond to the t instants while its columns matches the points in the Space. For this example, we have computed 614 intervals for 4184 sensible points:
In [10]: S.light
Out[10]:
array([[ True, True, True, ..., True, True, True],
[ True, True, True, ..., True, True, True],
[ True, True, True, ..., True, True, True],
...,
[ True, True, True, ..., False, False, False],
[ True, True, True, ..., True, True, True],
[ True, True, True, ..., True, True, True]], dtype=bool)
In [11]: S.light.shape
Out[11]: (614, 4184)
Note that for real computations where you probably have samples each 15 or 30 minutes, the number of rows will increase to 17500 - 35000.
On the other side, there is another version of the solution called light_vor stored in ShadowsManager.light_vor. In this case, the rows are the Voronoi’s diagram’s polygons, that is, the ON/OFF state of each point is referenced directly to the Solar Horizont discretization. Remember that each polygon of this discretization contains multiple (azimuth, zenit) pairs from the t and data vector.
In [12]: S.light_vor.shape
Out[12]: (277, 4184)
As we can see, the simulation has been made for 277 Sun positions that englobes the total 614 samples. However, if we run a simulation with a dt parameter considerably shorter the difference will be also considerably larger:
In [13]: S = space.shadows(init='auto', dt=15, resolution='high')
In [14]: S.light.shape # 35040 samples in t
Out[14]: (35040, 4184)
In [15]: S.light_vor.shape # 1139 polygons in the Voronoi's diagram
Out[15]: (1139, 4184)
In the next section we will see how we can control more specifically the parameters in order to generate more adjuted solutions, avoiding wasting resources.
Solar Horizont discretization¶
Finally, we are going to see a comparison between a coarse discretization and a much finer one.
The following visualizations are:
- vor: Voronoi diagram of the Solar Horizont. Samples in blue, polygon
centroinds in red. Polygons in semi-transparent blue.
- data: Accumulated time integral of the data projected
in the Voronoi diagram of the Solar Horizont.
- freq: Frequency of Sun positions in t in the Voronoi
diagram of the Solar Horizont.
In [16]: # Coarse discretization
...: S1 = space.shadows(init='auto', dt=856, resolution='mid')
...: S1.viz.vor_plot('vor')
...: S1.viz.vor_plot('data')
...: S1.viz.vor_plot('freq')
In [17]: # Fine discretization
...: S2 = space.shadows(init='auto', dt=13, resolution='mid')
...: S2.viz.vor_plot('vor')
...: S2.viz.vor_plot('data')
...: S2.viz.vor_plot('freq')
It is very clear that the discretization avoids the simulation to last 66 times longer for the second one, even when it has 66 times more samples. Instead of this, it groups the samples by proximity, and consequently, the execution time, which depends only to the number of polygons, is homogenized.
The correspondant exposure_plots for the previous examples are:
As you can see, the visualization is in practice the same but, as we have seen, the problem have been solved with different time resolutions. Does this mean that the solution is exactly the same? Of course not. If you have some pyny3d processes inside a larger software processing, for example photovoltaic electric generation, I am sure that you prefer to know the ON/OFF state of the solar cells each quarter hour than each 14 hours, even the visualization where a year is summed up looks the same.
Note
If you are curious about the left cut in the previous Solar Horizont discretization (at about -1.5 radians solar azimuth), remember that the 3D model has a lateral wall on this side. This wall prevents the Sun to fully illuminate the points in the first hours of the mornings.
Next tutorial: Advanced shading tutorial