Learning Time-Dependent Models¶
Time-Dependent Parameters¶
In addition to learning static parameters, QInfer can be used to learn the values of parameters that change stochastically as a function of time. In this case, the model parameter vector \(\vec{x}\) is interpreted as a time-dependent vector \(\vec{x}(t)\) representing the state of an underlying process. The resulting statistical problem is often referred to as state-space estimation. By using an appropriate resampling algorithm, such as the Liu-West algorithm [LW01], state-space and static parameter estimation can be combined such that a subset of the components of \(\vec{x}\) are allowed to vary with time.
QInfer represents state-space filtering by the use of
the Simulatable.update_timestep() method, which samples
how a model parameter vector is updated as a function of time.
In particular, this method is used by SMCUpdater to draw samples from the
distribution \(f\)
where \(t_{\ell}\) is the time at which the experiment \(e_{\ell}\)
is measured, and where \(t_{\ell+1}\) is the time step immediately
following \(t_{\ell}\). As this distribution is in general dependent
on the experiment being performed, update_timestep()
is vectorized in a manner similar to likelihood() (see
Designing and Using Models for details). That is,
given a tensor \(X_{i,j}\) of model parameter vectors and a vector
\(e_k\) of experiments,
update_timestep() returns a tensor \(X_{i,j,k}'\)
of sampled model parameters at the next time step.
Random Walk Models¶
As an example, RandomWalkModel implements update_timestep()
by taking as an input a Distribution specifying steps
\(\Delta \vec{x} = \vec{x}(t + \delta t) - \vec{x}(t)\). An
instance of RandomWalkModel decorates another model in
a similar fashion to other derived models.
For instance, the following code declares a precession model in
which the unknown frequency \(\omega\) changes by a normal
random variable with mean 0 and standard deviation 0.005 after
each measurement.
>>> from qinfer import (
... SimplePrecessionModel, RandomWalkModel, NormalDistribution
... )
>>> model = RandomWalkModel(
... underlying_model=SimplePrecessionModel(),
... step_distribution=NormalDistribution(0, 0.005 ** 2)
... )
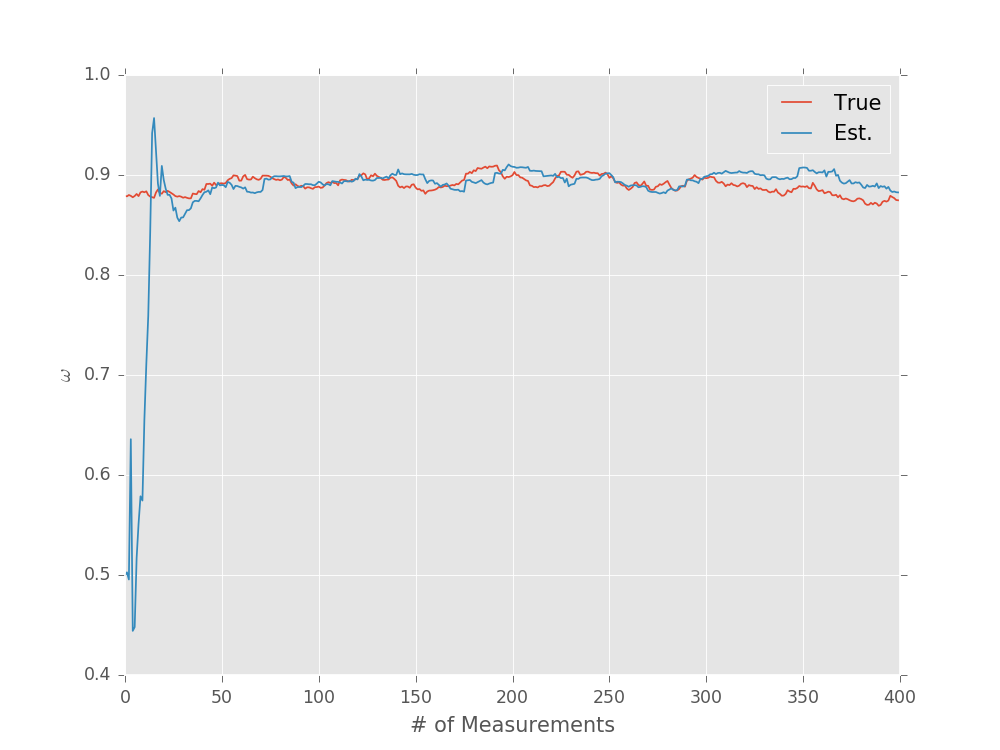
We can then draw simulated trajectories for the true and estimated value of \(\omega\) using a minor modification to the updater loop discussed in Sequential Monte Carlo.
model = RandomWalkModel(
# Note that we set a minimum frequency of negative
# infinity to prevent problems if the random walk
# causes omega to cross zero.
underlying_model=SimplePrecessionModel(min_freq=-np.inf),
step_distribution=NormalDistribution(0, 0.005 ** 2)
)
prior = UniformDistribution([0, 1])
updater = SMCUpdater(model, 2000, prior)
expparams = np.empty((1, ), dtype=model.expparams_dtype)
true_trajectory = []
est_trajectory = []
true_params = prior.sample()
for idx_exp in range(400):
# We don't want to grow the evolution time to be arbitrarily
# large, so we'll instead choose a random time up to some
# maximum.
expparams[0] = np.random.random() * 10 * np.pi
datum = model.simulate_experiment(true_params, expparams)
updater.update(datum, expparams)
# We index by [:, :, 0] to pull off the index corresponding
# to experiment parameters.
true_params = model.update_timestep(true_params, expparams)[:, :, 0]
true_trajectory.append(true_params[0])
est_trajectory.append(updater.est_mean())
plt.plot(true_trajectory, label='True')
plt.plot(est_trajectory, label='Est.')
plt.legend()
plt.xlabel('# of Measurements')
plt.ylabel(r'$\omega$')
plt.show()
(Source code, svg, pdf, hires.png, png)
Specifying Custom Time-Step Updates¶
The RandomWalkModel example above is somewhat unrealistic,
however, in that the step distribution is independent of the evolution
time. For a more reasonable noise process, we would expect that
\(\mathbb{V}[\omega(t + \Delta t) - \omega(t)] \propto \Delta t\).
We can subclass SimplePrecessionModel to add this behavior
with a custom update_timestep() implementation.
class DiffusivePrecessionModel(SimplePrecessionModel):
diffusion_rate = 0.0005 # We'll multiply this by
# sqrt(time) below.
def update_timestep(self, modelparams, expparams):
step_std_dev = self.diffusion_rate * np.sqrt(expparams)
steps = step_std_dev * np.random.randn(
# We want the shape of the steps in omega
# to match the input model parameter and experiment
# parameter shapes.
# The axis of length 1 represents that this model
# has only one model parameter (omega).
modelparams.shape[0], 1, expparams.shape[0]
)
# Finally, we add a new axis to the input model parameters
# to match the experiment parameters.
return modelparams[:, :, np.newaxis] + steps
model = DiffusivePrecessionModel()
prior = UniformDistribution([0, 1])
updater = SMCUpdater(model, 2000, prior)
expparams = np.empty((1, ), dtype=model.expparams_dtype)
true_trajectory = []
est_trajectory = []
true_params = prior.sample()
for idx_exp in range(400):
expparams[0] = np.random.random() * 10 * np.pi
datum = model.simulate_experiment(true_params, expparams)
updater.update(datum, expparams)
true_params = model.update_timestep(true_params, expparams)[:, :, 0]
true_trajectory.append(true_params[0])
est_trajectory.append(updater.est_mean())
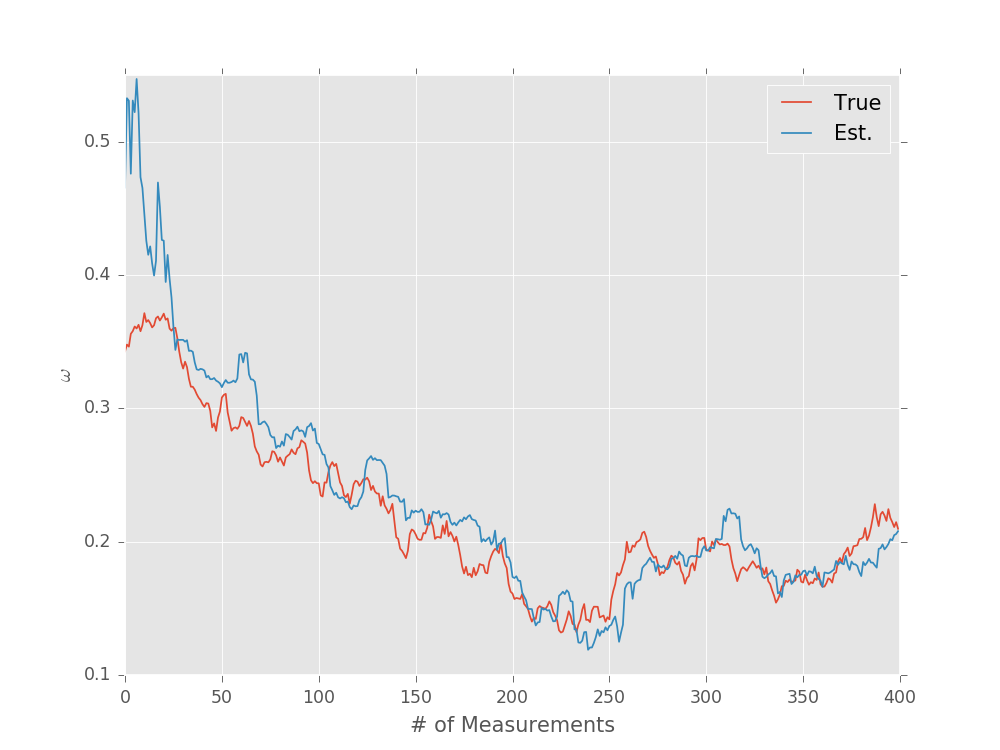
plt.plot(true_trajectory, label='True')
plt.plot(est_trajectory, label='Est.')
plt.legend()
plt.xlabel('# of Measurements')
plt.ylabel(r'$\omega$')
plt.show()
(Source code, svg, pdf, hires.png, png)