pymodelfit.builtins.Plane

class pymodelfit.builtins.Plane(varorder='xyz', vn=(1, 0, 0), wn=(0, 1, 0), origin=(0, 0, 0))

Bases: pymodelfit.core.FunctionModel

Models a plane of the form

i.e. (a,b,c) is the normal vector and d/a, b ,or c are the intercepts.

__init__(varorder='xyz', vn=(1, 0, 0), wn=(0, 1, 0), origin=(0, 0, 0))

Methods

__init__([varorder, vn, wn, origin])
chi2Data([x, y, weights, ddof])	Computes the chi-squared statistic for the data assuming this model.
distance(x, y, z)	compute the distance of a set of points in the 3D space from
f(x[, a, b, c, d])
fitData(x, y, z[, w])	Least squares fit using the output variable as the dependent variable.
getCov()	Computes the covariance matrix for the last fitData() call.
getMCMC(x, y[, priors, datamodel])	Generate an Markov Chain Monte Carlo sampler for the data and model.
inv(output, *args, **kwargs)	Compute the inverse of this model for the requested output.
isVarnumModel()	Determines if the model represented by this class accepts a variable number of parameters (i.e.
plot3d((data=array([[-1,  1],        [-1, ...)	data should be 3 x N
proj(x, y, z)	Project points onto the plane from the 3D space
resampleFit([x, y, xerr, yerr, bootstrap, ...])	Estimates errors via resampling.
residuals([x, y, retdata])	Compute residuals of the provided data against the model.
stdData([x, y])	Determines the standard deviation of the model from data.
unproj(v, w)	Extract points from the plane back into the 3D space

Attributes

data	The fitting data for this model.
defaultparval	int(x=0) -> int or long
errors	Error on the data.
fittype	str(object=’‘) -> string
fittypes	A Sequence of the available valid values for the fittype
fixedpars	tuple() -> empty tuple
n	non-normalized unit vector
nhat	normalized unit vector
origin
params	A tuple of the parameter names.
pardict	A dictionary mapping parameter names to the associated values.
parvals	The values of the parameters in the same order as params
rangehint
varorder
vn	3D vector to project on to plane to get 2D basis vector 1
weightstype	Determines the statistical interpretation of the weights in data.
wn	3D vector to project on to plane to get 2D basis vector 2

chi2Data(x=None, y=None, weights=None, ddof=1)

Computes the chi-squared statistic for the data assuming this model.

Parameters:

• x (array-like or None) – Input data value or None to use stored data
• y (array-like or None) – Output data value or None to use stored data
• weights (array-like or None) – Weights to adjust chi-squared, typically for error bars. Statistically interpreted based on the weightstype attribute. If None, any stored data will be used.
• ddof (int) – Delta Degrees of Freedom. The divisor used for the reduced chi-squared is n-m-ddof, where N is the number of points and m is the number of parameters in the model.

Returns:

tuple of floats (chi2,reducedchi2,p-value)

data None

The fitting data for this model. Should be either None, or a tuple(datain,dataout,weights). Note that the weights are interpreted statistically as errors based on the weightstype attribute.

distance(x, y, z)

compute the distance of a set of points in the 3D space from the plane

errors None

Error on the data. Sets the weights on data assuming the interpretation for errors given by weightstype. If data is None/missing, a TypeError will be raised.

fitData(x, y, z, w=None)

Least squares fit using the output variable as the dependent variable.

fittypes None

A Sequence of the available valid values for the fittype attribute. (Read-only)

getCov()

Computes the covariance matrix for the last fitData() call.

Returns:The covariance matrix with variables in the same order as params. Diagonal entries give the variance in each parameter.

Warning

This is not guaranteed to work for custom fit-types, but will always work with the default (leastsq) fit.

getMCMC(x, y, priors={}, datamodel=None)

Generate an Markov Chain Monte Carlo sampler for the data and model. This function requires the PyMC package for the MCMC internals and sampling.

Parameters:

• x (array-like) – Input data value
• y (array-like) – Output data value
• priors (dictionary) –

  Maps parameter names to the priors to assume for that parameter. There must be an entry for every parameter in the model. The prior specification can be in any of the following forms:

  • A pymc.Stochastric object
  • A 2-tuple (lower,upper) for a uniform prior
  • A scalar > 0 to use a gaussian prior of the provided width centered at the current value of the parameter
  • 0 for a Poisson prior with k set by the current value of the parameter
• datamodel –

  Specifies the model to assume for the fitting data points. May be any of the following:

  • None

    A normal distribution with sigma given by the data’s standard deviation.

  • A tuple (dist,dataname,kwargs)

    The first element is the pymc.distribution to be used as the distribution representing the data and the second is the name of the argument to be associated with the FunctionModel1D’s output, and the third is kwargs for the distribution (“observed” and “data” will be ignored, as will the data argument)

  • A sequence

    A normal distribution is used with sigma for each data point specified by the sequence. The length must match the model.

  • A scalar

    A normal distribution with the given standard deviation.

Raises ValueError:  

If a prior is not provided for any parameter.

Returns:

A pymc.MCMC object ready to sample for this model.

inv(output, *args, **kwargs)

Compute the inverse of this model for the requested output.

Parameters:output – The output value of the model at which to compute the inverse. Returns:The input value at which the model produces output Raises ModelTypeError:  If the model is not invertable for the provided data set.

classmethod isVarnumModel()

Determines if the model represented by this class accepts a variable number of parameters (i.e. number of parameters is set when the object is created).

Returns:True if this model has a variable number of parameters.

n None

non-normalized unit vector

nhat None

normalized unit vector

params None

A tuple of the parameter names. (read-only)

pardict None

A dictionary mapping parameter names to the associated values.

parvals None

The values of the parameters in the same order as params

Plane.plot3d(data=array([[-1, 1],

[-1, 1],

[-1, 1]]), n=10, showdata=False, clf=True, **kwargs)

data should be 3 x N

proj(x, y, z)

Project points onto the plane from the 3D space

Parameters:

• x (array-like length N) – first cartesian coordinate.
• y (array-like length N) – second cartesian coordinate.
• z (array-like length N) – third cartesian coordinate.

Returns:

A 2 x N array in the plane for each of the input points.

resampleFit(x=None, y=None, xerr=None, yerr=None, bootstrap=False, modely=False, n=250, prefit=True, medianpars=False, plothist=False, **kwargs)

Estimates errors via resampling. Uses the fitData function to fit the function many times while either using the “bootstrap” technique (resampling w/replacement), monte carlo estimates for the error, or both to estimate the error in the fit.

Parameters:

• x (array-like or None) – The input data - if None, will be taken from the data attribute.
• y (array-like or None) – The output data - if None, will be taken from the data attribute.
• xerr (array-like, callable, or None) – Errors for the input data (assumed to be normally distributed), or if None, will be taken from the data. Alternatively, it can be a function that accepts the input data as the first argument and returns corresponding monte carlo sampled values.
• yerr (array-like, callable, or None) – Errors for the output data (assumed to be normally distributed), or if None, will be taken from the data. Alternatively, it can be a function that accepts the output data as the first argument and returns corresponding monte carlo sampled values.
• bootstrap (bool) – If True, the data is also resampled (with replacement).
• modely – If True, the fitting data will be generated by offseting from model values (evaluated at the x-values) instead of y-values.
• n (int) – The number of times to draw samples.
• prefit (bool) – If True, the data will be fit without resampling once before the samples are recorded.
• medianpars (bool) – If True, the median from the histogram will be set as the value for the parameter.
• plothist (bool or string) – If True, histograms will be plotted using matplotlib.pyplot.hist() for each of the parameters, or if it is a string, only the histogram for the requested parameter will be shown.

kwargs are passed into fitData

Returns:(histd,cov) where histd is a dictionary mapping parameters to their histograms and cov is the covariance matrix of the parameters in parameter order.

Note

If x, y, xerr, or yerr are provided, they do not overwrite the stored data, unlike most other methods for this class.

residuals(x=None, y=None, retdata=False)

Compute residuals of the provided data against the model. E.g. .

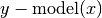Parameters:

• x (array-like or None) – Input data value or None to use stored data
• y (array-like or None) – Output data value or None to use stored data
• retdata (bool) – If True, returns the data along with the model.

Returns:

Residuals of model from y or if retdata is True, a tuple (x,y,residuals).

Return type:

array-like

stdData(x=None, y=None)

Determines the standard deviation of the model from data. Data can either be provided or (by default) will be taken from the stored data.

Parameters:

• x (array-like or None) – Input data value or None to use stored data.
• y (array-like or None) – Output data value or None to use stored data.

Returns:

standard deviation of model from y

unproj(v, w)

Extract points from the plane back into the 3D space

Parameters:

• x (array-like length N) – first in-plane coordinate.
• y (array-like length N) – second in-plane coordinate.

Returns:

a 3 x N (x,y,z) array

vn None

3D vector to project on to plane to get 2D basis vector 1

weightstype None

Determines the statistical interpretation of the weights in data. Can be:

• ‘ierror’

  Weights act as inverse errors (default)

• ‘ivar’

  Weights act as inverse variance

• ‘error’

  Weights act as errors (non-standard - this makes points with larger error bars count more towards the fit).

• ‘var’

  Weights act as variance (non-standard - this makes points with larger error bars count more towards the fit).

wn None

3D vector to project on to plane to get 2D basis vector 2