2. Global functions

pypol module has some functions to work with polynomials. If you need other utility functions check the pypol.funcs and pypol.roots modules.

polynomial() algebraic_fraction() monomial() poly1d()

poly1d_2() gcd() lcm()

pypol.poly1d(coeffs, variable='x', right_hand_side=True)

Make a 1 dimension polynomial from a list of coefficients.

Parameters:

• coeffs (list) – the list of the polynomial coefficients
• variable (string) – the letter of the polynomial, default x
• right_hand_side (bool or None) – if True, the last term of coeffs will be the right hand-side of the polynomial

Examples

We create the polynomials 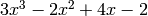, 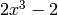and .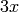

>>> poly1d([3, -2, 4, -2])
+ 3x^3 - 2x^2 + 4x - 2
>>> poly1d([2, 0, 0, -2])
+ 2x^3   - 2

pay attention here:

>>> poly1d([3], right_hand_side=False)
+ 3x

because if you don’t do this:

>>> poly1d([3])
+ 3

3 will be interpreted as the right_hand_side of the polynomial.

An alternative solution may be:

>>> poly1d([3, 0])
+ 3x

pypol.poly1d_2(monomials, variable='x')

Make a 1 dimension polynomial from a list of lists.

Parameters:

• monomials (list) – a list of lists that represents the polynomial’s monomial; evary sub-list has the coefficient and the power of the variable
• variable (string) – the letter of the polynomial (default x)

Return type:

Polynomial

Examples

We want to create these two polynomials: 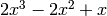and :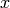

>>> poly1d_2([[-1, 7], [2, 3], [-2, 2], [1, 1]])
- x^7 + 2x^3 - 2x^2 + x
>>> poly1d_2([[1, 1]])
+ x

This function is very useful when you need a polynomial with negative powers or with spread powers:

>>> poly1d_2([[1, -1], [2, -3], [3, 5]])
+ 3x^5 + x^-1 + 2x^-3

or:

>>> poly1d_2([[2, 9], [1, 2]])
+ 2x^9 + x^2

in this case, if you want to use poly1d() or polynomial() you can do this:

>>> poly1d([2, 0, 0, 0, 0, 0, 0, 1, 0, 0])
+ 2x^9 + x^2
>>> poly1d([2, 0, 0, 0, 0, 0, 0, 1, 0], right_hand_side=False)
+ 2x^9 + x^2
>>> polynomial('2x^9 + x^2')
+ 2x^9 + x^2
>>> polynomial('2x9 x2')
+ 2x^9 + x^2

pypol.polynomial(string=None, simplify=True)

Returns a Polynomial object.

Parameters:

• string (string or None) – a string that represent a polynomial, default is None.
• simplify (bool) – if True, the polynomial will be simplified on __init__ and on update.

Return type:

Polynomial

Warning

With this function you cannot make polynomials with negative powers. In case you want to use negative powers, use poly1d_2() instead.

Examples

We want to make the polynomial :

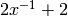>>> polynomial('2x^-1 + 2')
+ 2x + 1 ## Wrong!
>>> k = poly1d_2([[2, -1], [2, 0]])
>>> k
+ 2x^-1 + 2
>>> k.sort(key=k._key('x'))
>>> k
+ 2x^-1 + 2

2.1. polynomial()‘s syntax rules

Powers can be expressed using the ^ symbol. If a digit follows a letter then it is interpreted as an exponent. So the following expressions are equal:

>>> polynomial('2x^3y^2 + 1') == polynomial('2x3y2 + 1')
True

but if there is a white space after the letter then the digit is interpreted as a positive coefficient. So this:

>>> polynomial('2x3y 2 + 1')

represents this polynomial:

2x^3y + 3

>>> polynomial('2x3y 2 + 1')
+ 2x^3y + 3

pypol.algebraic_fraction(s1, s2='1', simplify=True)

Wrapper function that returns an AlgebraicFraction object.

Parameters s1, s2:  two strings that represent a polynomial

>>> algebraic_fraction('3x^2 - 4xy', 'x + y')
AlgebraicFraction(+ 3x² - 4xy, + x + y)
>>> algebraic_fraction('3x^2 - 4xy', 'x + y').terms
(+ 3x^2 - 4xy, + x + y)

See also

AlgebraicFraction

pypol.monomial(coeff=1, **vars)

Simple function that returns a Polynomial object.

Parameters:coeff – the coefficient of the polynomial Key **vars:the monomial’s letters

>>> monomial(5, a=3, b=4)
+ 5a^3b^4
>>> m = monomial(5, a=3, b=4)
>>> m
+ 5a^3b^4
>>> type(m)
<class 'pypol.src.pypol.Polynomial'>
>>> m.monomials
((5, {'a': 3, 'b': 4}),)

This function is useful when you need a monomial. Without it you should do:

>>> Polynomial(((5, {'a': 3, 'b': 4}),))
+ 5a^3b^4

Either coeff or **vars is optional:

>>> monomial()
+ 1
>>> monomial(1)
+ 1

Equivalent to:

def monomial(coeff=1, **vars):
    return Polynomial(((coeff, vars),))

New in version 0.2.

New in version 0.4: The *var parameter

pypol.parse_polynomial(string, max_length=None)

Parses a string that represent a polynomial. It can parse integer coefficients, float coefficient and fractional coefficient.

Parameters:

• string – a string that represent a polynomial
• max_length (integer or None) – represents the maximum length that the polynomial can have.

An example:

>>> parse_polynomial('2x^3 - 3y + 2')
[(2, {'x': 3}), (-3, {'y': 1}), (2, {})]
>>> parse_polynomial('x3 - 3y2 + 2')
[(1, {'x': 3}), (-3, {'y': 2}), (2, {})]

See also

polynomial()’s syntax rules

pypol.gcd(a, b)

Returns the Greatest Common Divisor between two polynomials:

>>> gcd(polynomial('3x'), polynomial('6x^2'))
+ 3x

pypol.lcm(a, b)

Returns the Least Common Multiple between two polynomials:

>>> lcm(polynomial('3x'), polynomial('6x^2'))
+ 6x^2

See also

pypol.funcs for other utility functions.