Navigation

5. The funcs module

New in version 0.3.

This module add some utility function to pypol.

Note

In all these examples it will be assumed that all items in the pypol.funcs namespace have been imported:

from pypol.funcs import *

5.1. Basic functions

The pypol.funcs module offers some basic functions for derivation, integration, interpolation and others.

pypol.funcs.divisible(a, b)

Returns True whether a and b are divisible, i.e. a % b == 0

Params a:the first polynomial
Params b:the second polynomial
Return type:bool

Examples

>>> a, b = poly1d([1, 7, 6]), poly1d([1, -5, -6])
>>> a, b
(+ x^2 + 7x + 6, + x^2 - 5x - 6)
>>> c = gcd(a, b)
>>> c
+ 12x + 12
>>> divisible(a, c)
True
>>> divisible(b, c)
True

New in version 0.3.

pypol.funcs.from_roots(roots, var='x')

Make a polynomial from its roots. These can be integer, float or fractions.Fraction objects but the complex type is not supported.

Examples

>>> p = from_roots([4, -2, 153, -52])
>>> p
+ x^4 - 103x^3 - 7762x^2 + 16720x + 63648
>>> p(4)
0
>>> p(-2)
0
>>> p(153)
0
>>> p(-52)
0
>>> roots.newton(p, 1000)
153.0
>>> roots.newton(p, 100)
-2.0
>>> roots.newton(p, 10)
4.0
>>> roots.newton(p, -10000)
-52.0

Note

From pypol 0.5 onwards, you can also construct a Polynomial using the classmethod from_roots().

pypol.funcs.random_poly(coeff_range=xrange(-10, 11), len_=None, len_range=xrange(-10, 11), letters='xyz', max_letters=3, unique=False, exp_range=xrange(1, 6), right_hand_side=None, not_null=None)

Returns a polynomial generated randomly.

Parameters:
  • coeff_range – the range of the polynomial’s coefficients, default is xrange(-10, 11).
  • len_ – the len of the polynomial. Default is None, in this case len_ will be a random number chosen in coeff_range. If len_ is negative it will be coerced to be positive: len_ = -len_.
  • letters – the letters that appear in the polynomial.
  • max_letter – is the maximum number of letter for every monomial.
  • unique –

    if True, all the polynomial’s monomials will have the same letter (chosen randomly). For example, if you want to generate a polynomial with a letter only, you can do:

    >>> random_poly(letters='x')
+ 3x^5 - 10x^4 - 4x^3 + x - 9
>>> random_poly(letters='x')
- 12x^4 - 6x^2
>>> random_poly(letters='z')
+ 8z^5 - 7z^3 + 10z^2 + 10
>>> random_poly(letters='y')
- 12y^5 - 15y^4 - y^3 + 9y^2 + 4y

    or:

    >>> random_poly(unique=True)
+ 6z^5 - 8z^4 + 6z^3 + 7z^2 + 2z
>>> random_poly(unique=True)
- 2z^5 + 3
>>> random_poly(unique=True)
- 19y^5 - y^4 - 8y^3 - 5y^2 - 4y
>>> random_poly(unique=True)
- 2x^4 - 10x^3 + 2x^2 + 3
  • exp_range – the range of the exponents.
  • right_hand_side – if True, the polynomial will have a right-hand side. Default is None, that means the right-hand side will be chosen randomly.
  • not_null – if True, the polynomial will not be an empty polynomial
Return type:

pypol.Polynomial

Some examples:

>>> random_poly()
 + 2x^4y^5 + 3y^5 + 5xy^5 + 10x^2y^3z^3 - 5z
>>> random_poly()
 + 7xy^5 - 3z^4 - 2
>>> random_poly(len_=3, letters='ab')
 + 9a^5 + 7a^2b^4 - 8ab^2
>>> random_poly(letters='abcdef', max_letters=1)
- 9
>>> random_poly(letters='abcdef', max_letters=1)
- 5e^5 + 2f^4 + 5a^2
>>> random_poly(letters='abcdef', max_letters=2)
- 9f^5 - d - 10
>>> random_poly(letters='abcdef', max_letters=2)
- 9de^5 - 4a^3d^5 - 5d^5 + 4af^3 + 2e^2f - 3f^2
>>> random_poly(letters='abcdef', max_letters=2, exp_range=xrange(0, 20, 5))
- 7e^15 + 5d^15 - 10c^15 - 9b^10 - 12e^5 - 12c^5 - 2f^5

New in version 0.2: The unique parameter.

New in version 0.3: The not_null parameter.

pypol.funcs.polyder(poly, m=1)

Returns the derivative of the polynomial poly.

Parameters:m (integer) – order of differentiation (default 1)
Return type:pypol.Polynomial

Examples

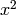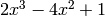Let’s calculate the derivative of the polynomials x^2 and 2x^3 - 4x^2 + 1:

>>> p1 = poly1d([1, 0, 0]) ## or poly1d([1, 0], right_hand_side=False)
>>> p1
 + x^2
>>> polyder(p1)
 + 2x
>>> p2 = poly1d([2, -4, 0, 1])
>>> p2
 + 2x^3 - 4x^2  + 1
>>> polyder(p2)
 + 6x^2 - 8x

New in version 0.3.

New in version 0.4: The m parameter.

pypol.funcs.polyint(poly, m=1, C=[])
Returns the indefinite integral of the polynomial poly:
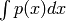
\int p(x)dx
Parameters:
  • poly (Polynomial) – the polynomial
  • m (integer) – the order of the antiderivative (default 1)
  • C (list of integers or integer - if m = 1) – integration costants. They are given in order of integration: those corresponding to highest-order terms come first.
Return type:

pypol.Polynomial

Examples

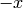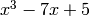Let’s calculate the indefinite integrals of the polynomials: -x and x^3 - 7x + 5:

>>> p1, p2 = poly1d([-1, 0]), poly1d([1, 0, -7, 5])
>>> p1, p2
(- x, + x^3 - 7x + 5)
>>> polyint(p1)
- 1/2x^2
>>> polyint(p2)
+ 1/4x^4 - 7/2x^2 + 5x
>>> polyder(polyint(p2))
+ x^3 - 7x + 5
>>> polyder(polyint(p1))
- x

The integration costants default to zero, but can be specified:

>>> polyder(p2)
+ 3x^2 - 7
>>> polyint(polyder(p2))
+ x^3 - 7x ## + 5 is missing!
>>> polyint(polyder(p2), [5])
+ x^3 - 7x + 5
>>> p = poly1d([1]*3)
>>> p
+ x^2 + x + 1
>>> P = polyint(p, 3, [6, 5, 3])
>>> P
+ 1/60x^5 + 1/24x^4 + 1/6x^3 + 3x^2 + 5x + 3
>>> polyint(p, 3, [6, 5, 3]) == polyint(polyint(polyint(p, C=[6]), C=[5]), C=[3])
True
>>> polyint(poly1d([1, 2, 3]))
+ 1/3x^3 + x^2 + 3x
>>> polyint(poly1d([1, 2, 3]), C=[2])
+ 1/3x^3 + x^2 + 3x + 2
>>> polyint(poly1d([1, 2, 3]), C=2)
+ 1/3x^3 + x^2 + 3x + 2
>>> polyint(poly1d([1, 2, 3]), 2, [4, 2])
+ 1/12x^4 + 1/3x^3 + 3/2x^2 + 4x + 2
>>> polyint(poly1d([1]*4), 3, [3, 2, 1])
+ 1/120x^6 + 1/60x^5 + 1/24x^4 + 1/6x^3 + 3/2x^2 + 2x + 1
>>> polyint(poly1d([1]*4), 3, [3, 2, 1, 5]) ## Take only the first 3
+ 1/120x^6 + 1/60x^5 + 1/24x^4 + 1/6x^3 + 3/2x^2 + 2x + 1

References

MathWorld

New in version 0.3.

pypol.funcs.polyint_(poly, a, b)
Returns the definite integral of the polynomial poly, with upper and lower limits:
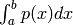
\int_{a}^{b}p(x)dx
Parameters:
  • a (integer) – the lower limit
  • b (integer) – the upper limit
Return type:

pypol.Polynomial

Examples

>>> p = poly1d([1, -3, -9, 1])
>>> p
+ x^3 - 3x^2 - 9x + 1
>>> q = (x - 4) * (x + 1) ** 3
>>> q
+ x^4 - x^3 - 9x^2 - 11x - 4
>>> polyint_(p, 2, 5)
56.25
>>> polyint_(p, 2, -3)
-23.75
>>> polyint_(q, -2, 5)
63.350000000000001
>>> polyint_(q, -2, -5)
523.35000000000002
>>> polyint_(q, -2, -2)
0.0
>>> polyint_(q, -2, 2)
51.200000000000003

References

Wikipedia
MathWorld
pypol.funcs.interpolate(x_values, y_values)

Interpolate with the Lagrange method.

Parameters:
  • x_values (list) – the list of the abscissas
  • y_values (list) – the list of the ordinates
Return type:

pypol.Polynomial

Examples

>>> interpolate([1, 2, 3], [1, 4, 9])
+ x^2
>>> p = interpolate([1, 2, 3], [1, 4, 9])
>>> p(1)
1
>>> p(2)
4
>>> p(3)
9
>>> p = interpolate([1, 2, 3], [1, 8, 27])
>>> p
+ 6x^2 - 11x + 6
>>> p(1)
1
>>> p(2)
8
>>> p(3)
27

but if we try with 4:

>>> p(4)
58

the result is not perfect: should be x^3 = 4^3 = 64, we can add one more value:

>>> p = interpolate([1, 2, 3, 4], [1, 8, 27, 64])
>>> p
+ x^3
>>> p(1)
1
>>> p(2)
8
>>> p(3)
27
>>> p(4)
64

We can try the cosine function too:

>>> import math
>>>
>>> x_v = [1, -32.2, 0.2, -12.2, 0.4]
>>> y_v = map(math.cos, x_v)
>>> y_v
[0.5403023058681398, 0.7080428643420057, 0.9800665778412416, 0.9336336440746373, 0.9210609940028851]
>>> p = interpolate(x_v, y_v)
>>> p ## A very long poly!
- 2417067429553017973005099476715844103379446789540038909310678504698270901105495/2707409624012905618588119802194467013735315173565700662238302437019821480374960128x^4 - 1942267679000251038989987154422384683928962465119931442239925165453801873763059175207737627343679/48772355895375265692471784351434957835024042172475236371981878692129204441317416127174693934333952x^3 - 12133766064251675639470092058084556745619727603471504062793227297260084623414714553791778090859658672043937021451/33792486744060501594993042946329990651637576923390278726204278046693250936252763136559703626455271403773983981568x^2 - 8449198638314223862904690273041499535188022044569033231622065815369263940698277030042252113946248523072534698219424954503422045/123652612450634556751613947964695531352620963102614623319086521485616582380529318624956122225181581909568555469636340836051451904x + 27464264348045643407214010143652897475518958796010450956562975494384484993333061039123466505868232298596969866565225313125932431546586323/27235073155919889010032712909016054859325624636397564063940286275647413113828884649402576122673520100673957703182051533535911984666509312
>>> p = p.to_float() ## Convert the coefficients into floats
>>> p ## A normal poly!
- 0.000892760152773x^4 - 0.0398231260997x^3 - 0.359066977111x^2 - 0.068330126399x + 1.00841529563
>>> p(1)
0.5403023058675271

Let’s find the error:

>>> sum(((p(x_v[i]) - y_v[i]) ** 2) for i in xrange(len(x_v)))
2.617743433523715e-19

Another example with the tangent function:

>>> import math
>>> import random
>>> 
>>> x_v = [random.randrange(-100, 100, int=float) for _ in xrange(20)]
>>> x_v
[-52.04883772799136, 86.66510205351244, -69.71941509152728, -65.82564821655141, -39.88514562573457, -26.334754833643956, 67.29058857824606, 83.42212578407015, -65.01610969623977, 88.62441652980385, -46.64696595564377, 6.090284135651046, 48.561049399406755, 74.55661451495163, 31.601335697628656, -6.667427123777131, -3.5713119709399876, -21.080329311384077, -36.03494555679694, -83.51784709811665]
>>> y_v = map(math.tan, x_v)
>>> y_v
[4.633510066894531, -3.595019481676671, -0.6905813491675517, 0.1488831639192735, 1.4149405698827482, -2.587567026478643, 3.8574703132881716, -5.828356862239949, 1.4202891548496936, 0.7758201032224186, 0.5167071849006064, -0.19533000245833287, 7.438373910836117, -1.1192508506455194, 0.18756336443741384, -0.40433961413350117, -0.4582813476602284, 1.2885466130394196, -10.678941407170345, 3.6755014649680127]
>>> p = interpolate(x_v, y_v)
>>> len(p)
20
>>> p ## Very long poly!!
- 12219488143403815004684028301879843984580132115510309248714982646809732317034782564367156403823334665490477778807366943013783006674554991651417939218795355286657812942668102853104914548661705426201861138581721901730470132896281303417586590700230072859932217072822550515990416486500191967/718914949710333854052436960225398536144423045775367682693693995040482771293811786687676364630013288169823557994223803721156972481092714033911190094080738394015207814944249727177529194975693264945139221364416975697373163651177352995660773299843456348886005090013688532455309116749965319305754441403088068092373237760x^19 + 22523684961268899006755200379657843240660824727139256496632126417173528884606027022344147973197224707222378884506663993666643214513961151889056506243602001666115496448150520504469565153315171245725647218150202725999379464174936318080936617049033600889247040095711114886713315026153137051495409240666511/141649598108661055715920948054511953570339202012003736727145979962413664772479940146104153317222301624852225259791018604689136685027533100395407441642203002311725271238601660762625618408509738942908683580142569790453263348066148555721766067439426132813301057164989556815170834701236489347838045408664494021358053899854322589499392x^18 + 53896122738619728745780688585893525781366684808997907993452071642785292604776092622791484742797596212108047594271826214503417289882287829766271382403597482262853432025653586349834772466584378838328148981613440087734190334940777387522360270318870372410859731463627343257945979662915698923999710903299593623120041911221447/99677043321772882108205357205986290208878970186677198630565651964958801825187204914144018482338152290809932730143134302481185883532018897019823657852647903776255580128300817735149723673612271101098460297809843366689888517557382822543789086312835596524073863467148349063609164053681381787372220143169856611634440930276077516576181723444679802880x^17 + 2398855081931261908680085300027966530525425061222797332896909814652057556720438952850482306670230873719017798764984537174364238414559138184542131720374510785080047660449594941986574305230572797035530560043425082057723398177335679774441338144065485058911909787045596660865355403291779591428857174916746420554786756573125917343251989527/4676098907930511861289293605019200737241772695813462240211495170544065924590514494766001326387603239754095465026079459771377964647130574919588626149804346941133866248749705857406564792637867978080297469597534319267191269586751553821930789859441050824382311304175848976204798179589710623330071470558707405291293866970093641016449416066365480616605850145914880x^16 - 2359837727576612092680559254420221102673730876686933763768683429740491786221656732182764808307358827153024649497942839652535829135219420560890276779909517567422303931606826502446115491111723348106912574715923047940089150177556619806126931041331442191976767759570529167949964772396065340790698984968797636432365651181187055558516014954502088142303167503/329051207801616195334596270956534310805708848719209700364112164958186793746174147736927254438336556803153708717652755526703775662317076472157159081361081416266671598738115584773010803262827143774544240539614645182303587346871375602358297395556315138139682675954915403134315567179663635665820574996763036119189496007261008662089145385670028571961655966088908596834541240320x^15 - 1809870568964664663822089943313264209051663989848776965575767589723013304284631710805314990681756038989308683387541800780024981251799450839269216091127509615457086588924420975593233328810660179958463182235450259076449918405126310118737792391856926456426493335607044554383296425744726826709097485651966368954670440614907681726840458683029386403894748179844299065228419/23154920263143286618620539062220709927525071509042252186088587928718040868436628105638297097727612684055207749278575540166262311311320400367551329512902620775362018203275121545510862577148439347409019050767192776714450789962415573084752900721153626023193139167954980485669539944535593311685157758812365553558907181103654678358353419764401434852735302702778735849268899845532493000212480x^14 + 49545010867594835476202972093376908741954065327858855748988010847970187642945477764483338538994091284827888885117138657538510861383145823038387529324407047750614484332758175976883175672598262431480025764505428627690967228466265708736268721948712121133496450190496337987336703633995996122090551625806290411474315206069886542798230139458443914583007249495229653628090994311123523250783/977629596270802995009253932133205196203190311499181340309274538600015771092190065743274828495635864559667425525470817863070164873768062099353691814552237174910517550222114755002965659303308400406311591855581331643262531732995505739138120530380288548812512331870469741473977506776475505606434035034027778240667085232600639369640610099670524110844454842398425862604384275789855219462257272268922028032x^13 + 44346815768216448871342349070380235232465195256234273693961629936677409623401755782575924155542283086926451605609586051715101341728698836835391107820949155779069166781291152281386996083118482866767704232567866990420331996009185932099339897262039026848473240386240730293144638589586259337550400662949988934986944751858905030251019899149978698517751752228875752114265785721206906685807725086594728607/42996604350308172013809631804124363093503649369631094654994234048230987386113828181846582480166552750166600020668546843896411794290296780861657180982935096830731311151493328985055128470720386297315137525815518970633651328362269708949284197426068620904376730634038948329352276240840506150140915995161267760119864814568082423002075910672099342656065663908352750405288139271516904818332648353107843354331496872673280x^12 - 93560843039411956267141747750516765152046010406702744380581028699772649732084427589162996430158706903412265373311839394222558012598308503259668084386708038387657143866199758138667020692376072314360969411638974853758430089046762639576343581002985276638633673900766034534856170313382678783794148388174198624917874770078880263880326549473204938504171061989549450239502373591844863268197871644074492014987895008436813/465479546466933968129367002741563057775039570800240651665107135077068554182397426639211504603279455014658440309295155043417118545385640134964513978362352246099865232390588761457851532622164415932145155539246498316638660078375619386178611421951709132670490784907512601905125189014620112024981440961176029091024561813059157693931782588752714027627818825292948348858338517944435621902830156376326010830708657888291953284145479680x^11 - 105529311444245455256457632481181258150448353915772871700964114625893822096462205975993668408847820636122585096507713377243044320849860582438730658096342843052465945159637752252910909620875169249323522447342311842860512027506389613768708787489748974773051447009086129344349131782018747845120031642795868413460619864250139051347590758078213060819327182454785186562387455605195392999093078798576124129363062839645775149728227535051/17742406026186150298004676923006446079899098632197346591954070298214011178273595775501410198510594237287489278364522225933952201459591447306287088673324379443339155729493498656362515794236588567979050582122946841110027789596325933653981522695284335827364304111488191917107158876738187271608300278550306855858337315196691882061598167284242168721902926566606547702394140896658760933547348342937954377029264189948902528696142641093169895178240x^10 + 1061482456193442719900206994959924949487660859489723257552132957078797297822230532535470007629727966539764886409687219670014153549409722127807250269808562527134097214050199852918933846608605158663789364593191233500610765849457636997526704173604359426664505898413318145579727013357400596035720016407463207692309054240910589769247104819611700723465758421576702354034297183294490725952695035634545402271096673440637691510223990707116793203187662751/2497021661505874661804302055484902470790480907638077398398395634971906710557934210125080651513327457359489604010844596700821840242152201640404921255165304416129396208252538040277301580809162364881387358235781330819942897875923400353399322055951253366361646302384623523402442024650886659633352507998904589899403912075877922925551720398171578394367989792448993299046294357710126903507952939841562430881160997462817776331706668313681277378962682375013662720x^9 + 74911904106706499382386923066967255114226383541263504936437372866833968096123620642833862193206101526740076011883999832826226018319874283902618981500895637094101977927039940580681841085781317889204252905268864957862605125940901655407639667612134875304535496896050047005163780730028439501161690843011917861093962303888428499811114315821524399996599832254393890827143403583264306196076330237568187981393141535738516710577663335682609754525176367768097424507113/4392806962614810126059330633897260455442313529924787826867352383927702814969555085642470796333922032639116232490421441400151777346592942776294067809644647850459189911007664616237851058464544184041298994270419793051243155851083313282648035597878114459129109453808142273038655136731784814808241099855820233704338117533841469216216384252593368023249185483911272025099051932202729676216895714314881459067636509332906526864229575996367075618877161146416860748011276337152x^8 - 499864599086835423772323949562359160180875870478578170623623364390531814837946848603412100572886782888500518761712564661905966064588902880670518031127376468440673519701928782058202143540279513333995264103438600508141003716958935305527783406135418249563509292413411558627813184829491066051455017032814285158303944112600157610223823755997510372868913245912911650586640303212845842064440595051600414198088824565196042550051806385950621282363450530569733791689928805725586845921/1324784183031869145322604538961195547275999067617358249244439484292683690712014496575246304558350698245478022387823836533613644054988414712586179050670146652393513141424554213287851331239294770919439281151939921604924731264970205012222821557735796754451023257298796103121735775220443950751332904503388561572907942927264267131680952195312464610193811934321764469980724256258902299299037377960226809877926107517543498395541138482814498846022722755333485210760539264072780755364741120x^7 - 666036100924532675630261816153632045516187865757933353201377520936667062718957893245813739538764393057111885967175680484202029185581249442696678404757761676869549957005305586190682245267964493316951425572992593184698547183486142102614539641664723971316160285906426573916632961594125314638798697809673718877665672195807218012238670598428194801833104759677318783045726713813468710903869069609106472762499761139813473569507950107784142170195415639882230523367582868280148883389010461355473/29085567608517400862905780546886934278456304604766165832848254609205555076415134935958374586989668818006096183670777388014542701517371766216299913592519631466436946805253591841200902955663651618856620389414023054627692213393466921784009526257747731092216641780880815355434585276789231633924886262008443651845050473477032726179552941377162533024713540037054075049473107079047041147734387216591653369100344367391357879934019098777767822845594786554186294223192157462128921335456511960452956160x^6 - 81108891990264554007767676307940435070870452389341408758467881418844445737491720698663738888818937405943254784021059936160743624783670163284892499129819097249078383375331831499851005016686949073599882762783073488547457123908672644724690508707564245922150403543164250277719474922659510666520227866729617332440911234230302038079198582070921584378080573700404882938143264987018024824683496807971796506047720904288269600690039826781701696877553628790027237495531465876458139416808141575988703420424121575493/2870005921277464379093614434881148536732793570380585929426662837195251883240814045993724496947894261047004999849235648563432829795488893983676183845933279348940244740717136720734806477493923379188119683452283520670679518844901594536160059341964705952714184050548785778042892899823715119655976369046650671242572963994358726445657384575020818579392433443644364946810396590219663925975673061300362549234258679257461646997494881876817038683977947752595114816464760938909522978577125868499033457169716258841559040x^5 + 181832175330953716860577754196657426490341549424222031611096056849691713264532858881764029570026076790698338683801550168068574917706748116752727084430949810174114852565726704448116022919812618888425172987960997832163137689417024680915286312384893628640616901011166897783234077048746025396880321252761652267914673262223358480140907068569788269793505830168898138582753162523195729259012292238655918451103188184310460342339794560826737035758037054222100484615208684616833135856511829782685594239446756075597942446216698131/16829892705229564654949744804178677230504076732421039227160276877547082007895663711519384283307018468369712732980499853554064568954005050697182368388938325199162741308915850994096372271411692820265343757191072560196687898672971837263953570877655302762719836750413613423553385663110431544856774350171055897700076971690060811709520265175871862535017378051835503276358905675480227864816954968573624841426713081466813559915229336355242368646146955649833256640622852190309929091002728746842719991335250675471656171456042106880x^4 + 2114783763911986555564834543565844615201283791297340043976677146865181930801522678412950968912265101124566108499541908757296043129756230922132926916879458324898179401089323456042182810080916047371359778144836774291803130801966225221311477273732061733738013570485809269093225177186199764881279470591439478834444550124797507978634697857656640977467838000616814544078007920254519680207529987139367636477705727577459399227021922786430342224772029380719264382663836590739347966860432551353403729736351757887402624867772887550270974858543/14803730178897909425218903748094636614769635975254611227235636047742917411664258953459657516412936816417981772813522427237887322425300709573267511619238771689762132071117171350661736033885072673799712251767484716893750446555008172068395971907982856709500958075593806669280949766785961394505032261229841835296717252626745146274529974431665630796699093713776983929582049246113048120118626430224061739438268142730311259989042489750640601392901523645644035097528314926617213655026837056399062142662718468733475354902583203972820294959104x^3 + 39604228607714433128788515520321358397896593502185193363693279730649537974896152074538809526210556111504923562246023596220669477980160125204877711166402461079656468677440164445056301807849397910580355190745076597210562032876401068688809836067518893037151358596434430411748337392079990742674789918326748539384451465240182919475467674704825643741850567534664740899902179838863855156706856191276242586507212994927658421610899678051525409810819239721515531023406166653895303075477790962966383334549438594049744489128924737459066865650996990571065/1005521140766439294384299577154829427817795996565940809050681032621993413070214798524738857922388361118416952625352541607821591317937700778328413160498299019528722032911711831140744270664093315760777036907569263576281086019040860342604129845737006904671256313719084406407743133500918609585008365922360923675312239591342404171923748222805518961929418147144333630113269617046705864368472446054851842936345462948557148073865244653550866037143766930983328299116493124893606213133598896484698015970277307706956704158796513390420575911784579854237696x^2 - 56650171208529605535804554632831452231557080796913426690941454381302314650742317332788154285325371685956553205986241660329825283601493235288696423095854205403194640886619978080707476849308203630661122380094283544568751543229807991119963330210704678458027517205057375143292208709600909450900747969824196095021183043195890605558203897232053839038771376372655159131116577225026144334128963210582291106949484498496115046684047685436491978501487958185880508354606224364645300351544829527081672098560698163925379216850287689275165456168760981764105126338106475/10706416512765729170869303958563108095924660905272997800946590520710418580488890295254146879001212734425717114313909425959762712840468360823171299048927614587430417867511956671604083768835662408351722902466586371591501393504604490522915558052805163577260495620828096367250279648494413459817003943647005837232754278911449583034135033523496455233756615288026472749969096698861151800501780028634654575868565972181350142742253749819965497379267142124624759123143856258802022604472684410114716396823989563658093160815387989112353385320252996069828803193470976x - 5198052262522265546889354422418215379439773334988279064799758191663748711573759726797820682398780342262092783354041132013372143191322674406525406016343035378402443568894182214265407623898868368606968632065726192050891064251226591693367455614588721683913787157361493551958243257073944687114950698576362591443545774780969574826913938971886834304370566600779446588655540294025432649697694280593602190076104771744609290031077313192211079339771475539592979199137210277036841691966490133881934505800907413564977655703360974414027898655631045286678592137031949628279375/344699406974873132980295605880701690626100783690595987050981059912261537681346228292547107919089148976793658074884718525819110757340429973204637706531898983403776797711456361076928617659265031034113650131039666975452235685632045817865656954819338536728401355123926676402762650391124642055745306818621146146360556487065006600264070852437934942960195913992158183827654492256776466328363602028332316579799533281718257998768568208233730519388465271043240548056566654848443014891654951652764785346389339161492957288641040887175281427882507533275113406954502646398976
>>> p = p.to_float()
>>> p
- 1.69971262224e- 29x^19 + 1.5900987551e-28x^18 + 5.40707478297e-25x^17 + 5.13003494828e-25x^16 - 7.17164280703e- 21x^15 - 7.81635414157e- 20x^14 + 5.06787141639e-17x^13 + 1.03140274536e-15x^12 - 2.00998827445e- 13x^11 - 5.94785798998e- 12x^10 + 4.25099418462e-10x^9 + 1.70533111845e-08x^8 - 3.7731775899e- 07x^7 - 2.28991955697e- 05x^6 - 2.82608796689e- 05x^5 + 0.0108041197003x^4 + 0.142854789864x^3 + 0.0393867687133x^2 - 5.29123550732x - 15.0799570795
>>> sum((p(x_i) - y_v[i]) ** 2 for i, x_i in enumerate(x_v)) ## The error
1.280750397031077e-06
>>> p(x_v[0])
4.633512966735273
>>> y_v[0]
4.633510066894531

When we convert the polynomial coefficients into float numbers, we lose precision; if we re-compute the polynomial we can see that the error is much smaller!

>>> p = interpolate(x_v, y_v)
>>> sum((p(x_i) - y_v[i]) ** 2 for i, x_i in enumerate(x_v))
7.731095950923788e-14
>>> sum((p.to_float()(x_i) - y_v[i]) ** 2 for i, x_i in enumerate(x_v))
1.280750397031077e-06
>>> p = interpolate(x_v, y_v)
>>> sum((p.to_float()(x_i) - y_v[i]) ** 2 for i, x_i in enumerate(x_v))
1.280750397031077e-06
>>> sum((p(x_i) - y_v[i]) ** 2 for i, x_i in enumerate(x_v))
7.731095950923788e-14
pypol.funcs.divided_diff(p, x_values)

Computes the divided difference p[x_{0},x_{1},\ldots,x_{n}]:

>>> from pypol import *
>>> from pypol.funcs import divided_diff
>>> 
>>> p = poly1d([1, -43, 2, 4])
>>> p
+ x^3 - 43x^2 + 2x + 4
>>> divided_diff(p, [1, -4, 3])
-43.0
>>> divided_diff(p, [1, -4, 3, 4])
1.0
>>> divided_diff(p, [1])
-36
>>> divided_diff(p, [0]) ## divided_diff(p, [x_0]) == p(x_0)
4

New in version 0.4.

5.2. Numbers

Also, this module provides some functions to generate integer series, or numbers. Some of them are used in pypol.series: the stirling2() function is used in pypol.series.touchard() and pypol.series.bell().

pypol.funcs.bin_coeff(n, k)

Returns the binomial coefficient 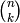\binom{n}{k}, i.e. the coefficient of the 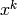x^k term of the binomial power (1 + x)^n.

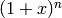Parameters:
  • n (integer) – the power of the binomial. If n == 1 the result will be (-1)^k
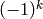
  • k (integer) – the power of the term
Return type:

integer

Examples

>>> bin_coeff(1, 4)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "funcs.py", line 367, in bin_coeff
    
ValueError: k cannot be greater than n
>>> bin_coeff(6, 4)
15
>>> bin_coeff(16, 9)
11440
>>> bin_coeff(-1, 9)
-1
>>> bin_coeff(-1, 8)
1
>>> bin_coeff(124, 98)
396167055763370435149824000L

It is the same as:

>>> def bin_coeff_2(n, k):
    if n < k:
        raise ValueError('k cannot be greater than n')
    return ((1 + x) ** n).get(k)

>>> bin_coeff(5, 4)
5
>>> bin_coeff_2(5, 4)
5
>>> bin_coeff_2(3, 4)
Traceback (most recent call last):
  File "<pyshell#18>", line 1, in <module>
    bin_coeff_2(3, 4)
  File "<pyshell#15>", line 3, in bin_coeff_2
    raise ValueError('k cannot be greater than n')
ValueError: k cannot be greater than n
>>> bin_coeff(3, 4)
Traceback (most recent call last):
  File "<pyshell#19>", line 1, in <module>
    bin_coeff(3, 4)
  File "funcs.py", line 388, in bin_coeff
    raise ValueError('k cannot be greater than n')
ValueError: k cannot be greater than n
>>> bin_coeff(56, 54)
1540
>>> bin_coeff_2(56, 54)
1540

When using large numbers, bin_coeff() approximate a bit, bin_coeff_2() does not (but it is slower):

>>> bin_coeff(123, 54)
307481607132479749691410373710708736L
>>> bin_coeff_2(123, 54)
307481607132479763736986522890815830L

but bin_coeff() is faster.

References

Wikipedia
pypol.funcs.harmonic(n)

Returns the n-th Harmonic number.

Raises :ValueError if n is negative or equal to 0
Return type:fractions.Fraction

Examples

>>> harmonic(0)
Traceback (most recent call last):
  File "<pyshell#1>", line 1, in <module>
    harmonic(0)
  File "funcs.py", line 469, in harmonic
    raise ValueError('Hamonic numbers only defined for n > 0')
ValueError: Hamonic numbers only defined for n > 0
>>> harmonic(1)
Fraction(1, 1)
>>> harmonic(2)
Fraction(3, 2)
>>> harmonic(3)
Fraction(11, 6)
>>> harmonic(4)
Fraction(25, 12)
>>> harmonic(5)
Fraction(137, 60)
>>> harmonic(6)
Fraction(49, 20)
>>> harmonic(26)
Fraction(34395742267, 8923714800)

References

MathWorld

pypol.funcs.harmonic_g(n, m)

Returns the n-th generalized Harmonic number of order m.

Raises :ValueError if n is negative or equal to 0
Return type:fractions.Fraction

Examples

>>> harmonic_g(0, 2)
Traceback (most recent call last):
  File "<pyshell#2>", line 1, in <module>
    harmonic_g(0, 2)
  File "funcs.py", line 654, in harmonic_g
    raise ValueError('Generalized Hamonic number only defined for n > 0')
ValueError: Generalized Hamonic number only defined for n > 0
>>> harmonic_g(1, 2)
Fraction(1, 1)
>>> harmonic_g(1, 3)
Fraction(1, 1)
>>> harmonic_g(2, 3)
Fraction(9, 8)
>>> harmonic_g(2, 4)
Fraction(17, 16)
>>> harmonic_g(3, 4)
Fraction(1393, 1296)
>>> harmonic_g(3, 7)
Fraction(282251, 279936)
>>> harmonic_g(7, 7)
Fraction(774879868932307123, 768464444160000000)

References

MathWorld

pypol.funcs.stirling(n, k)

Returns the signed Stirling number of the first kind s(n, k):

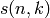>>> stirling(0, 0)
1.0
>>> stirling(0, 1)
0.0
>>> stirling(1, 1)
1.0
>>> stirling(2, 1)
-1.0
>>> stirling(2, 4)
0.0
>>> stirling(22, 4)
2.8409331590181146e+20
>>> stirling(12, 4)
105258076.0
>>> stirling(9, 4)
-67284.0

References

Wikipedia

pypol.funcs.stirling2(n, k)

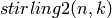Returns the Stirling numbers of the second kind stirling2(n, k):

>>> stirling2(0, 0)
1
>>> stirling2(0, 1)
0
>>> stirling2(1, 1)
1
>>> stirling2(2, 1)
1
>>> stirling2(3, 1)
1
>>> stirling2(3, 2)
3
>>> stirling2(6, 4)
65
>>> stirling2(96, 56)
601077471204201702246363542619610633289432609630600146569048337999099263354225431674880L
>>> stirling2(961, 2)
9745314011399999080353382387875188310876226857595007526867906457212948690766426102465615065882010259225304916231408668183459169865203094046577987296312653419531277699956473029870789655490053648352799593479218378873685597925394874945746363615468965612827738803104277547081828589991914110975L

References

Wikipedia

pypol.funcs.bell_num(n)

Returns the n-th Bell number B_n:

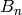>>> bell_num(0)
1
>>> bell_num(1)
1
>>> bell_num(2)
2
>>> bell_num(3)
5
>>> bell_num(4)
15
>>> bell_num(5)
52
>>> bell_num(6)
203
>>> bell_num(7)
877
>>> bell_num(8)
4140

References

MathWorld

pypol.funcs.entringer(func)

Returns the Entringer number E(n, k).

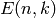Raises :ValueError if either n or k is negative or when k is greater than n
Return type:int 
>>> e(0, 0)
1
>>> e(1, 0)
0
>>> e(2, 0)
0
>>> e(2, 1)
1
>>> e(4, 1)
2
>>> e(4, 4)
5
>>> e(9, 4)
5296
>>> e(9, 8)
7936
>>> e(19, 8)
18164255316224L
>>> e(19, 18)
29088885112832L

New in version 0.5.

pypol.funcs.lucas_num(n)

Returns the Lucas number L_n:

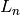>>> lucas_num(1)
1
>>> lucas_num(2)
3
>>> lucas_num(3)
4
>>> lucas_num(4)
7
>>> lucas_num(5)
11
>>> lucas_num(15)
1364
>>> lucas_num(152)
58360810951903342376540834889728L
>>> lucas_num(524)
32323880385391491573521580616521303413074220353619291180174372332058562230682094134384498459616996023833985024L
pypol.funcs.pell_num(n)

Returns the Pell number P_n:

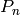>>> pell_num(0)
0
>>> pell_num(1)
1
>>> pell_num(2)
2
>>> pell_num(3)
5
>>> pell_num(4)
12
>>> pell_num(14)
80782
>>> pell_num(144)
4657508918199769652922062468973916916612976254692360192L
pypol.funcs.pell_lucas_num(n)

Returns the Pell-Lucas number Q_n:

>>> pell_lucas_num(0)
2
>>> pell_lucas_num(1)
2
>>> pell_lucas_num(2)
6
>>> pell_lucas_num(3)
14
>>> pell_lucas_num(4)
34
>>> pell_lucas_num(5)
82
>>> pell_lucas_num(6)
198
>>> pell_lucas_num(64)
3145168096065826821505024L
pypol.funcs.jacobsthal_num(n)

Returns the Jacobsthal number J_n:

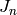>>> jacobsthal_num(0)
0
>>> jacobsthal_num(1)
1
>>> jacobsthal_num(2)
1
>>> jacobsthal_num(3)
3
>>> jacobsthal_num(4)
5
>>> jacobsthal_num(5)
11
>>> jacobsthal_num(6)
21
>>> jacobsthal_num(7)
43
>>> jacobsthal_num(71)
787061080478274158592L
pypol.funcs.jacobsthal_lucas_num(func)

Returns the Jacobsthal-Lucas number j_n:

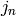>>> jacobsthal_lucas_num(0)
2
>>> jacobsthal_lucas_num(1)
1
>>> jacobsthal_lucas_num(2)
5
>>> jacobsthal_lucas_num(3)
7
>>> jacobsthal_lucas_num(4)
17
>>> jacobsthal_lucas_num(42)
4398046511105L
>>> jacobsthal_lucas_num(142)
5575186299632655785383929568162090376495105L
pypol.funcs.fermat_num(n)

Returns the Fermat number F_n:

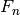>>> fermat_num(0)
3
>>> fermat_num(1)
5
>>> fermat_num(2)
17
>>> fermat_num(3)
257
>>> fermat_num(4)
65537
>>> fermat_num(5)
4294967297L
>>> fermat_num(6)
18446744073709551617L
>>> fermat_num(7)
340282366920938463463374607431768211457L
pypol.funcs.fermat_lucas_num(n)

Returns the Fermat-Lucas number f_n:

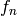>>> fermat_lucas_num(0)
0
>>> fermat_lucas_num(1)
1
>>> fermat_lucas_num(2)
3
>>> fermat_lucas_num(3)
7
>>> fermat_lucas_num(4)
15
>>> fermat_lucas_num(5)
31
>>> fermat_lucas_num(6)
63
>>> fermat_lucas_num(16)
65535
>>> fermat_lucas_num(162)
5846006549323611672814739330865132078623730171903L

Table Of Contents

Previous topic

4. Operators

Next topic

6. The roots module

This Page

Navigation

© Copyright 2010, Michele Lacchia. Created using Sphinx 1.0.7.