New in version 0.4.

7. The series module

This module implements the most common polynomial sequences, like Fibonacci’s sequence (fibonacci())

7.1. Lucas polynomials sequences

class pypol.series.LucasSeq(p, q, type='W')

“The Lucas polynomial sequence is a pair of generalized polynomials which generalize the Lucas sequence to polynomials ...” [MathWorld]

Parameters:

• p – The p parameter
• q – The q parameter
• zero (pypol.Polynomial) – The first element of the sequence (at index 0)
• one (pypol.Polynomial) – The second element of the sequence (at index 1)

Setting different values for p and q we obtain some polynomial sequences, for every p and q pair there are two polynomials sequences, 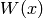and :

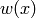p	q	W(x)	w(x)
x	1	Fibonacci polynomials (fibonacci())	Lucas polynomials (lucas())
2x	1	Pell polynomials (pell())	Pell-Lucas polynomials (pell_lucas())
1	2x	Jacobsthal polynomials (jacobsthal())	Jacobsthal-Lucas polynomials (jacob_lucas())
3x	-2	Fermat polynomials (fermat())	Fermat-Lucas polynomials (fermat_lucas())
2x	-1	Chebyshev polynomials of the second kind 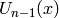(chebyshev_u())	Chebyshev polynomials of the first kind 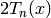(chebyshev_t())

The starting value for the 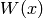polynomials is always 2, for the 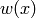polynomials is always a null polynomial.

[MathWorld]

Weisstein, Eric W. “Lucas Polynomial Sequence. “ From MathWorld – A Wolfram Web Resource.

New in version 0.4.

LucasSeq.__call__(n)

Returns the n-th element of the sequence

Parameters:n (integer) – the n-th element of the sequence Raises :ValueError if n is negative Return type:pypol.Polynomial

>>> from pypol import *
>>> from pypol.series import *
>>> 
>>> fibo = LucasSeq(x, ONE)
>>> fibo(0)

>>> fibo(1)
+ 1
>>> fibo(12)
+ x^11 + 10x^9 + 36x^7 + 56x^5 + 35x^3 + 6x
>>> fibo(19)
+ x^18 + 17x^16 + 120x^14 + 455x^12 + 1001x^10 + 1287x^8 + 924x^6 + 330x^4 + 45x^2 + 1
>>> f = fibo(45)
>>> f = fibo(65) ## Almost instantaneous

LucasSeq.cache

The cache used to speed up the calculation

LucasSeq.reset_cache()

Resets the cache, i.e. sets it to list containing only the first 2 values of the series (self.zero and self.one)

pypol.series.fibonacci(n)

Returns the n-th Fibonacci polynomial.

Raises :ValueError if n is negative Return type:pypol.Polynomial

Examples

>>> fibonacci(0)

>>> fibonacci(1)
+ 1
>>> fibonacci(2)
+ x
>>> fibonacci(3)
+ x^2 + 1
>>> fibonacci(4)
+ x^3 + 2x
>>> fibonacci(5)
+ x^4 + 3x^2 + 1
>>> fibonacci(6)
+ x^5 + 4x^3 + 3x
>>> fibonacci(23)
+ x^22 + 21x^20 + 190x^18 + 969x^16 + 3060x^14 + 6188x^12 + 8008x^10 + 6435x^8 + 3003x^6 + 715x^4 + 66x^2 + 1
>>> fibonacci(100)
+ x^99 + 98x^97 + 4656x^95 + 142880x^93 ... + 197548686920970x^17 + 22057981462440x^15 + 1889912732400x^13 + 119653565850x^11 + 5317936260x^9 + 154143080x^7 + 2598960x^5 + 20825x^3 + 50x
>>> fibonacci(200)
+ x^199 + 198x^197 + ... + 15913388077274800x^13 + 249145778809200x^11 + 2747472247520x^9 + 19813501785x^7 + 83291670x^5 + 166650x^3 + 100x
>>> len(fibonacci(300))
150
>>> len(str(fibonacci(300)))
8309

The Fibonacci polynomials are the W-polynomials in the Lucas sequence (LucasSeq) obtained setting p = x and q = 1:

>>> from pypol import x, ONE
>>> from pypol.series import LucasSeq
>>> 
>>> fibonacci_poly = LucasSeq(x, ONE)
>>> fibonacci_poly(0) ## A null polynomial

>>> fibonacci_poly(1)
+ 1
>>> fibonacci_poly(2)
+ x
>>> fibonacci_poly(3)
+ x^2 + 1
>>> fibonacci_poly(6)
+ x^5 + 4x^3 + 3x
>>> fibonacci_poly(16)
+ x^15 + 14x^13 + 78x^11 + 220x^9 + 330x^7 + 252x^5 + 84x^3 + 8x
>>> fibonacci_poly(24)
+ x^23 + 22x^21 + 210x^19 + 1140x^17 + 3876x^15 + 8568x^13 + 12376x^11 + 11440x^9 + 6435x^7 + 2002x^5 + 286x^3 + 12x
>>> fibonacci_poly(54)
+ x^53 + 52x^51 + 1275x^49 + 19600x^47 + 211876x^45 + 1712304x^43 + 10737573x^41 + 53524680x^39 + 215553195x^37 + 708930508x^35 + 1917334783x^33 + 4280561376x^31 + 7898654920x^29 + 12033222880x^27 + 15084504396x^25 + 15471286560x^23 + 12875774670x^21 + 8597496600x^19 + 4537567650x^17 + 1855967520x^15 + 573166440x^13 + 129024480x^11 + 20160075x^9 + 2035800x^7 + 118755x^5 + 3276x^3 + 27x
>>> fibonacci_poly(54) ## Instantaneous
+ x^53 + 52x^51 + 1275x^49 + 19600x^47 + 211876x^45 + 1712304x^43 + 10737573x^41 + 53524680x^39 + 215553195x^37 + 708930508x^35 + 1917334783x^33 + 4280561376x^31 + 7898654920x^29 + 12033222880x^27 + 15084504396x^25 + 15471286560x^23 + 12875774670x^21 + 8597496600x^19 + 4537567650x^17 + 1855967520x^15 + 573166440x^13 + 129024480x^11 + 20160075x^9 + 2035800x^7 + 118755x^5 + 3276x^3 + 27x

New in version 0.3.

pypol.series.lucas(n)

Returns the n-th Lucas polynomial.

Raises :ValueError if n is negative Return type:pypol.Polynomial

Examples

>>> lucas(0)
+ 2
>>> lucas(1)
+ x
>>> lucas(2)
+ x^2 + 2
>>> lucas(3)
+ x^3 + 3x
>>> lucas(4)
+ x^4 + 4x^2 + 2
>>> lucas(14)
+ x^14 + 14x^12 + 77x^10 + 210x^8 + 294x^6 + 196x^4 + 49x^2 + 2

The Lucas polynomials are the w-polynomials obtained setting p = x and q = 1 in the Lucas polynomial sequence (see LucasSeq). You can generate them with this small piece of code:

>>> from pypol import x, ONE
>>> 
>>> lucas_poly = LucasSeq(x, ONE, 'w')
>>> lucas_poly(0)
+ 2
>>> lucas_poly(1)
+ x
>>> lucas_poly(2)
+ x^2 + 2
>>> lucas_poly(5)
+ x^5 + 5x^3 + 5x
>>> lucas_poly(15)
+ x^15 + 15x^13 + 90x^11 + 275x^9 + 450x^7 + 378x^5 + 140x^3 + 15x

References

MathWorld

New in version 0.4.

pypol.series.pell(n)

Returns the n-th Pell polynomial.

Raises :ValueError if n is negative Return type:pypol.Polynomial

Examples

>>> pell(0) # A null polynomial

>>> pell(1)
+ 1
>>> pell(2)
+ 2x
>>> pell(3)
+ 4x^2 + 1
>>> pell(4)
+ 8x^3 + 4x
>>> pell(14)
+ 8192x^13 + 24576x^11 + 28160x^9 + 15360x^7 + 4032x^5 + 448x^3 + 14x

The Pell polynomials are the W-polynomials obtained setting p = 2x and q = 1 in the Lucas sequence (see LucasSeq). We can easily generate them:

>>> from pypol import x, ONE
>>> from pypol.series import LucasSeq
>>> 
>>> def pell_poly(n):
    return LucasSeq(n, 2*x, ONE)

>>> pell_poly(0)

>>> pell_poly(1)
+ 1
>>> pell_poly(3)
+ 4x^2 + 1
>>> pell_poly(9)
+ 256x^8 + 448x^6 + 240x^4 + 40x^2 + 1

References

MathWorld

New in version 0.4.

pypol.series.pell_lucas(n)

Returns the n-th Pell-Lucas polynomial.

Raises :ValueError if n is negative Return type:pypol.Polynomial

Examples

>>> pell_lucas(0)
+ 2
>>> pell_lucas(1)
+ 2x
>>> pell_lucas(2)
+ 4x^2 + 2
>>> pell_lucas(3)
+ 8x^3 + 6x
>>> pell_lucas(4)
+ 16x^4 + 16x^2 + 2
>>> pell_lucas(5)
+ 32x^5 + 40x^3 + 10x
>>> pell_lucas(8)
+ 256x^8 + 512x^6 + 320x^4 + 64x^2 + 2
>>> pell_lucas(12)
+ 4096x^12 + 12288x^10 + 13824x^8 + 7168x^6 + 1680x^4 + 144x^2 + 2

The Pell polynomials are the w-polynomials obtained setting p = 2x and q = 1 in the Lucas sequence (see LucasSeq). We can easily generate them:

>>> from pypol import x, ONE, TWO
>>> from pypol.series import LucasSeq
>>> 
>>> def pell_lucas_poly(n):
    return LucasSeq(n, 2*x, ONE, TWO, 2*x)

>>> pell_lucas_poly(0)
+ 2
>>> pell_lucas_poly(1)
+ 2x
>>> pell_lucas_poly(2)
+ 4x^2 + 2
>>> pell_lucas_poly(4)
+ 16x^4 + 16x^2 + 2
>>> pell_lucas_poly(8)
+ 256x^8 + 512x^6 + 320x^4 + 64x^2 + 2

References

MathWorld

New in version 0.4.

pypol.series.jacobsthal(n)

Returns the n-th Jacobsthal polynomial.

Raises :ValueError if n is negative Return type:pypol.Polynomial

Examples

>>> jacobsthal(0) ## A null polynomial

>>> jacobsthal(1)
+ 1
>>> jacobsthal(2)
+ 1
>>> jacobsthal(3)
+ 2x + 1
>>> jacobsthal(4)
+ 4x + 1
>>> jacobsthal(5)
+ 4x^2 + 6x + 1
>>> jacobsthal(6)
+ 12x^2 + 8x + 1
>>> jacobsthal(16)
+ 1024x^7 + 5376x^6 + 8064x^5 + 5280x^4 + 1760x^3 + 312x^2 + 28x + 1

The Jacobsthal polynomials are the W-polynomials in the Lucas sequence (see LucasSeq), obtained setting p = 1 and q = 2x:

>>> from pypol import x, ONE
>>> from pypol.series import LucasSeq
>>> 
>>> def jacobsthal_poly(n):
    return LucasSeq(n, ONE, 2*x)

>>> jacobsthal_poly(0)

>>> jacobsthal_poly(1)
+ 1
>>> jacobsthal_poly(2)
+ 1
>>> jacobsthal_poly(3)
+ 2x + 1
>>> jacobsthal_poly(4)
+ 4x + 1
>>> jacobsthal_poly(5)
+ 4x^2 + 6x + 1
>>> jacobsthal_poly(7)
+ 8x^3 + 24x^2 + 10x + 1
>>> jacobsthal_poly(9)
+ 16x^4 + 80x^3 + 60x^2 + 14x + 1
>>> jacobsthal_poly(11)
+ 32x^5 + 240x^4 + 280x^3 + 112x^2 + 18x + 1

References

MathWorld

New in version 0.4.

pypol.series.jacob_lucas(n)

Returns the n-th Jacobsthal-Lucas polynomial.

Raises :ValueError if n is negative Return type:pypol.Polynomial

Examples

>>> jacob_lucas(0)
+ 2
>>> jacob_lucas(1)
+ 1
>>> jacob_lucas(2)
+ 4x + 1
>>> jacob_lucas(3)
+ 6x + 1
>>> jacob_lucas(4)
+ 8x^2 + 8x + 1
>>> jacob_lucas(5)
+ 20x^2 + 10x + 1
>>> jacob_lucas(6)
+ 16x^3 + 36x^2 + 12x + 1
>>> jacob_lucas(9)
+ 144x^4 + 240x^3 + 108x^2 + 18x + 1
>>> jacob_lucas(10)
+ 64x^5 + 400x^4 + 400x^3 + 140x^2 + 20x + 1

The Jacobsthal-Lucas polynomials are the w-polynomials in the Lucas sequence (see LucasSeq), obtained setting p = 1 and q = 2x:

>>> from pypol import x, ONE, TWO
>>> from pypol.series import LucasSeq
>>> 
>>> def jacob_lucas_poly(n):
    return LucasSeq(n, ONE, 2*x, TWO, ONE)

>>> jacob_lucas_poly(0)
+ 2
>>> jacob_lucas_poly(1)
+ 1
>>> jacob_lucas_poly(2)
+ 4x + 1
>>> jacob_lucas_poly(3)
+ 6x + 1
>>> jacob_lucas_poly(4)
+ 8x^2 + 8x + 1
>>> jacob_lucas_poly(5)
+ 20x^2 + 10x + 1
>>> jacob_lucas_poly(15)
+ 1920x^7 + 8960x^6 + 12096x^5 + 7200x^4 + 2200x^3 + 360x^2 + 30x + 1

References

MathWorld

New in version 0.4.

pypol.series.fermat(n)

Returns the n-th Fermat polynomial.

Raises :ValueError if n is negative Return type:pypol.Polynomial

Examples

>>> fermat(0)

>>> fermat(1)
+ 1
>>> fermat(2)
+ 3x
>>> fermat(3)
+ 9x^2 - 2
>>> fermat(5)
+ 81x^4 - 54x^2 + 4
>>> fermat(6)
+ 243x^5 - 216x^3 + 36x
>>> fermat(7)
+ 729x^6 - 810x^4 + 216x^2 - 8
>>> fermat(9)
+ 6561x^8 - 10206x^6 + 4860x^4 - 720x^2 + 16
>>> fermat(11)
+ 59049x^10 - 118098x^8 + 81648x^6 - 22680x^4 + 2160x^2 - 32

The Fermat polynomials are the W-polynomials in the Lucas sequence (see LucasSeq), obtained setting p = 3x and q = -2:

>>> from pypol import x, TWO
>>> from pypol.series import LucasSeq
>>> 
>>> def fermat_poly(n):
    return LucasSeq(n, 3*x, -TWO)

>>> fermat_poly(0)

>>> fermat_poly(1)
+ 1
>>> fermat_poly(2)
+ 3x
>>> fermat_poly(3)
+ 9x^2 - 2
>>> fermat_poly(4)
+ 27x^3 - 12x
>>> fermat_poly(5)
+ 81x^4 - 54x^2 + 4
>>> fermat_poly(7)
+ 729x^6 - 810x^4 + 216x^2 - 8

References

MathWorld

New in version 0.4.

pypol.series.fermat_lucas(n)

Returns the n-th Fermat-Lucas polynomial.

Raises :ValueError if n is negative Return type:pypol.Polynomial

Examples

>>> fermat_lucas(0)
+ 2
>>> fermat_lucas(1)
+ 3x
>>> fermat_lucas(2)
+ 9x^2 - 4
>>> fermat_lucas(3)
+ 27x^3 - 18x
>>> fermat_lucas(4)
+ 81x^4 - 72x^2 + 8
>>> fermat_lucas(5)
+ 243x^5 - 270x^3 + 60x
>>> fermat_lucas(9)
+ 19683x^9 - 39366x^7 + 26244x^5 - 6480x^3 + 432x

The Fermat-Lucas polynomials are the w-polynomials in the Lucas sequence (see LucasSeq), obtained setting p = 3x and q = -2:

>>> from pypol import x, TWO
>>> from pypol.series import LucasSeq
>>> 
>>> def fermat_lucas_poly(n):
    return LucasSeq(n, 3*x, -TWO, TWO, 3*x)

>>> fermat_lucas_poly(0)
+ 2
>>> fermat_lucas_poly(1)
+ 3x
>>> fermat_lucas_poly(2)
+ 9x^2 - 4
>>> fermat_lucas_poly(3)
+ 27x^3 - 18x
>>> fermat_lucas_poly(4)
+ 81x^4 - 72x^2 + 8
>>> fermat_lucas_poly(5)
+ 243x^5 - 270x^3 + 60x
>>> fermat_lucas_poly(6)
+ 729x^6 - 972x^4 + 324x^2 - 16
>>> fermat_lucas_poly(7)
+ 2187x^7 - 3402x^5 + 1512x^3 - 168x
>>> fermat_lucas_poly(8)
+ 6561x^8 - 11664x^6 + 6480x^4 - 1152x^2 + 32

References

MathWorld

New in version 0.4.

pypol.series.chebyshev_t(n)

Returns the n-th Chebyshev polynomial of the first kind in x.

Raises :ValueError if n is negative Return type:pypol.Polynomial

Examples

>>> chebyshev_t(0)
 + 1
>>> chebyshev_t(1)
 + x
>>> chebyshev_t(2)
 + 2x^2 - 1
>>> chebyshev_t(4)
 + 8x^4 - 8x^2 + 1
>>> chebyshev_t(5)
 + 16x^5 - 20x^3 + 5x
>>> chebyshev_t(9)
 + 256x^9 - 576x^7 + 432x^5 - 120x^3 + 9x

Chebyshev polynomials of the first kind are the w-polynomials of Lucas sequence (see LucasSeq), obtained setting p = 2x and q = 1:

>>> from pypol import x, ONE
>>> from pypol.series import LucasSeq
>>> 
>>> chebyshev_t_poly = LucasSeq(2*x, -ONE, 'w')
>>> _chebyshev_t = lambda n: chebyshev_t_poly(n) / 2
>>> 
>>> _chebyshev_t(0)
+ 1
>>> _chebyshev_t(1)
+ x
>>> _chebyshev_t(2)
+ 2x^2 - 1
>>> _chebyshev_t(3)
+ 4x^3 - 3x
>>> _chebyshev_t(4)
+ 8x^4 - 8x^2 + 1

New in version 0.3.

pypol.series.chebyshev_u(n)

Returns the n-th Chebyshev polynomial of the second kind in x.

Raises :ValueError if n is negative Return type:pypol.Polynomial

Examples

>>> chebyshev_u(0)
 + 1
>>> chebyshev_u(1)
 + 2x
>>> chebyshev_u(2)
 + 4x^2 - 1
>>> chebyshev_u(4)
 + 16x^4 - 12x^2 + 1
>>> chebyshev_u(6)
 + 64x^6 - 80x^4 + 24x^2 - 1
>>> chebyshev_u(8)
 + 256x^8 - 448x^6 + 240x^4 - 40x^2 + 1
>>> chebyshev_u(11)
 + 2048x^11 - 5120x^9 + 4608x^7 - 1792x^5 + 280x^3 - 12x

Chebyshev polynomials of the second kind are the W-polynomials of the Lucas sequence (see LucasSeq), obtained setting p = 2x and q = 1:

>>> from pypol import x, ONE
>>> from pypol.series import LucasSeq
>>> 
>>> chebyshev_u_poly = LucasSeq(2*x, -ONE)
>>> _chebyshev_u = lambda n: chebyshev_u_poly(n + 1)
>>> 
>>> _chebyshev_u(0)
+ 1
>>> _chebyshev_u(1)
+ 2x
>>> _chebyshev_u(2)
+ 4x^2 - 1
>>> _chebyshev_u(3)
+ 8x^3 - 4x
>>> _chebyshev_u(4)
+ 16x^4 - 12x^2 + 1
>>> _chebyshev_u(5)
+ 32x^5 - 32x^3 + 6x

New in version 0.3.

7.2. Bernoulli and Euler sequences

pypol.series.bernoulli(m)

Returns the m-th Bernoulli polynomial.

Raises :ValueError if m is negative Return type:pypol.Polynomial

Examples

>>> bernoulli(0)
+ 1
>>> bernoulli(1)
+ x - 1/2
>>> bernoulli(2)
+ x^2 - x + 1/6
>>> bernoulli(3)
+ x^3 - 3/2x^2 + 1/2x
>>> bernoulli(4)
+ x^4 - 2x^3 + x^2 - 1/30
>>> bernoulli(5)
+ x^5 - 5/2x^4 + 5/3x^3 - 1/6x
>>> bernoulli(6)
+ x^6 - 3x^5 + 5/2x^4 - 1/2x^2 + 1/42
>>> bernoulli(16)
+ x^16 - 8x^15 + 20x^14 - 182/3x^12 + 572/3x^10 - 429x^8 + 1820/3x^6 - 1382/3x^4 + 140x^2 - 3617/510
>>> bernoulli(36)
+ x^36 - 18x^35 + 105x^34 - 3927/2x^32 + 46376x^30 - 1008678x^28 + 19256580x^26 - 316816590x^24 + 4429013400x^22 - 51828575337x^20 + 498870877450x^18 - 3866772293937x^16 + 23507139922200x^14 - 108370572082590x^12 + 362347726769028x^10 - 826053753510678x^8 + 1171754413536680x^6 - 1780853160521127/2x^4 + 270657225128535x^2 - 26315271553053477373/1919190

References

Wikipedia | MathWorld

pypol.series.bern_num(m)

Returns the m-th Bernoulli number.

Raises :ValueError if m is negative Return type:fractions.Fraction

Note

If m is odd, the result is always 0.

Examples

>>> bern_num(0)
+ 1
>>> bern_num(1)
- 1/2
>>> bern_num(2)
Fraction(1, 6)
>>> bern_num(3)
0
>>> bern_num(4)
Fraction(-1, 30)
>>> bern_num(6)
Fraction(1, 42)
>>> bern_num(8)
Fraction(-1, 30)
>>> bern_num(10)
Fraction(5, 66)

References

Wikipedia | MathWorld

pypol.series.euler(m)

Returns the m-th Euler polynomial.

Raises :ValueError if m is negative Return type:pypol.Polynomial

Examples

>>> euler(0)
+ 1
>>> euler(1)
+ x - 1/2
>>> euler(2)
+ x^2 - x
>>> euler(3)
+ x^3 - 3/2x^2 + 1/4
>>> euler(4)
+ x^4 - 2x^3 + x
>>> euler(5)
+ x^5 - 5/2x^4 + 5/2x^2 - 1/2
>>> euler(15)
+ x^15 - 15/2x^14 + 455/4x^12 - 3003/2x^10 + 109395/8x^8 - 155155/2x^6 + 943215/4x^4 - 573405/2x^2 + 929569/16

References

MathWorld

pypol.series.euler_num(m)

Returns the m-th Euler number.

Raises :ValueError if m is negative Return type:Integer

Note

If m is odd, the result is always 0.

Examples

>>> euler_num(0)
+ 1
>>> euler_num(2)
-1
>>> euler_num(3)
0
>>> euler_num(4)
5
>>> euler_num(6)
-61
>>> euler_num(8)
1385
>>> euler_num(10)
-50521

References

Wikipedia | MathWorld

pypol.series.genocchi(n)

Returns the n-th Genocchi number.

Return type:integer or fractions.Fraction

Note

If n is odd, the result is always 0.

Examples

>>> genocchi(0)
0
>>> genocchi(2)
-1
>>> genocchi(8)
17
>>> genocchi(17)
0
>>> genocchi(34)
-14761446733784164001387L

Should be quite fast:

>>> from timeit import timeit
>>> timeit('(genocchi(i) for i in xrange(1000))', 'from pypol.series import genocchi', number=1000000)
1.8470048904418945

7.3. Other series

pypol.series.hermite_prob(n)

Returns the n-th probabilistic Hermite polynomial, that is a polynomial of degree n.

Raises :ValueError if n is negative Return type:pypol.Polynomial

Examples

>>> hermite_prob(0)
 + 1
>>> hermite_prob(1)
 + x
>>> hermite_prob(2)
 + x^2 - 1
>>> hermite_prob(4)
 + x^4 - 6x^2 + 3
>>> hermite_prob(45)
 + x^45 - 990x^43 + .. cut .. + 390756386568644372393927184375x^5 - 186074469794592558282822468750x^3 + 25373791335626257947657609375x

New in version 0.3.

pypol.series.hermite_phys(n)

Returns the n-th Hermite polynomial (physicist).

Raises :ValueError if n is negative Return type:pypol.Polynomial

Examples

>>> hermite_phys(0)
 + 1
>>> hermite_phys(1)
 + 2x
>>> hermite_phys(2)
 + 4x^2 - 2
>>> hermite_phys(3)
 + 8x^3 - 12x
>>> hermite_phys(4)
 + 16x^4 - 48x^2 + 12
>>> hermite_phys(9)
 + 512x^9 - 9216x^7 + 48384x^5 - 80640x^3 + 30240x
>>> hermite_phys(11)
 + 2048x^11 - 56320x^9 + 506880x^7 - 1774080x^5 + 2217600x^3 - 665280x

New in version 0.3.

pypol.series.laguerre(n)

Returns the n-th Laguerre polynomial in x.

Raises :ValueError if n is negative Return type:pypol.Polynomial

Examples

>>> laguerre(0)
+ 1
>>> laguerre(1)
- x + 1
>>> laguerre(2)
+ 1/2x^2 - 2x + 1
>>> laguerre(3)
- 1/6x^3 + 3/2x^2 - 3x + 1
>>> laguerre(4)
+ 1/24x^4 - 2/3x^3 + 3x^2 - 4x + 1
>>> laguerre(14)
+ 1/87178291200x^14 - 1/444787200x^13 + 13/68428800x^12 - 13/1425600x^11 + 143/518400x^10 - 143/25920x^9 + 143/1920x^8 - 143/210x^7 + 1001/240x^6 - 1001/60x^5 + 1001/24x^4 - 182/3x^3 + 91/2x^2 - 14x + 1

Should be approximatively like a generalized Laguerre polynomial with a = 0 (laguerre_g()):

>>> laguerre(5), laguerre_g(5)(a=0)
(- 1/120x^5 + 5/24x^4 - 5/3x^3 + 5x^2 - 5x + 1, - 833333333333/100000000000000x^5 + 208333333333/1000000000000x^4 - 166666666667/100000000000x^3 + 5x^2 - 5x + 1)

References

Wikipedia | MathWorld

pypol.series.laguerre_g(n, a='a')

Returns the n-th generalized Laguerre polynomial in x.

Raises :ValueError if n is negative Return type:pypol.Polynomial

Examples

>>> l(0)
+ 1
>>> l(1)
+ a + 1 - x
>>> l(2)
+ 1/2a^2 + 3/2a - ax + 1 - 2x + 1/2x^2
>>> l(3)
+ 1/6a^3 + a^2 - 1/2a^2x + 11/6a - 5/2ax + 1/2ax^2 + 1 - 3x - 1/6x^3 + 3/2x^2
>>> l(2, 'k')
+ 1/2k^2 + 3/2k - kx + 1 - 2x + 1/2x^2
>>> l(2, 'z')
+ 1/2x^2 - 2x - xz + 1 + 3/2z + 1/2z^2
>>> l(5, 'z')
- 1/120x^5 + 5/24x^4 + 1/24x^4z - 5/3x^3 - 3/4x^3z - 1/12x^3z^2 + 5x^2 + 47/12x^2z + x^2z^2 + 1/12x^2z^3 - 5x - 77/12xz - 71/24xz^2 - 7/12xz^3 - 1/24xz^4 + 1 + 137/60z + 15/8z^2 + 17/24z^3 + 1/8z^4 + 1/120z^5
>>> l(5)
+ 1/120a^5 + 1/8a^4 - 1/24a^4x + 17/24a^3 - 7/12a^3x + 1/12a^3x^2 - 71/24a^2x + 15/8a^2 + a^2x^2 - 1/12a^2x^3 + 47/12ax^2 - 77/12ax + 137/60a - 3/4ax^3 + 1/24ax^4 + 5x^2 - 5/3x^3 - 5x + 1 - 1/120x^5 + 5/24x^4
>>> l(6)
+ 1/720a^6 + 7/240a^5 - 1/120a^5x + 35/144a^4 - 1/6a^4x + 1/48a^4x^2 - 31/24a^3x + 49/48a^3 + 3/8a^3x^2 - 1/36a^3x^3 + 119/48a^2x^2 - 29/6a^2x + 203/90a^2 - 5/12a^2x^3 + 1/48a^2x^4 - 37/18ax^3 + 57/8ax^2 + 49/20a - 87/10ax + 11/48ax^4 - 1/120ax^5 + 5/8x^4 - 10/3x^3 + 1 - 6x + 15/2x^2 - 1/20x^5 + 1/720x^6

References

Wikipedia

MathWorld

New in version 0.4.

pypol.series.abel(n, variable='a')

Returns the n-th Abel polynomial in x and variable.

Raises :ValueError if n is negative Return type:pypol.Polynomial

Examples

>>> abel(0)
 + 1
>>> abel(1)
 + x
>>> abel(2)
 + x^2 - 2ax
>>> abel(5)
 + x^5 - 20ax^4 + 150a^2x^3 - 500a^3x^2 + 625a^4x
>>> abel(9)
 + x^9 - 72ax^8 + 2268a^2x^7 - 40824a^3x^6 + 459270a^4x^5 - 3306744a^5x^4 + 14880348a^6x^3 - 38263752a^7x^2 + 43046721a^8x

New in version 0.3.

pypol.series.gegenbauer(n, a='a')

Returns the n-th Gegenbauer polynomial in x.

Raises :ValueError if n is negative Return type:pypol.Polynomial

Examples

>>> gegenbauer(0)
+ 1
>>> gegenbauer(1)
+ 2ax
>>> gegenbauer(2)
+ 2a^2x^2 + 2ax^2 - a
>>> 
>>> 
>>> gegenbauer(4)
+ 2/3a^4x^4 + 4a^3x^4 - 2a^3x^2 + 22/3a^2x^4 + 1/2a^2 - 6a^2x^2 + 4ax^4 - 4ax^2 + 1/2a

References

Wikipedia

MathWorld

New in version 0.4.

pypol.series.touchard(n)

Returns the n-th Touchard polynomial in x.

Return type:pypol.Polynomial

Examples

>>> touchard(0)
+ 1
>>> touchard(1)
+ x
>>> touchard(2)
+ x^2 + x
>>> touchard(12)
+ x^12 + 66x^11 + 7498669301432319/4398046511104x^10 + 22275x^9 + 159027x^8 + 627396x^7 + 1323652x^6 + 1379400x^5 + 611501x^4 + 86526x^3 + 2047x^2 + x

The Touchard polynomials also satisfy:

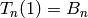
where 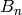is the n-th Bell number (funcs.bell_num()):

>>> long(touchard(19)(1)) == long(bell_num(19))
True

The more n become greater, the more it loses precision:

>>> long(touchard(23)(1)) == long(bell_num(23))
False
>>> abs(long(touchard(23)(1)) - long(bell_num(23)))
8L
>>> long(touchard(45)(1)) == long(bell_num(45))
False
>>> abs(long(touchard(45)(1)) - long(bell_num(45)))
19342813113834066795298816L
>>> long(touchard(123)(1)) == long(bell_num(123))
False
>>> abs(long(touchard(123)(1)) - long(bell_num(123)))
429106803807439187983719223678319701219747465049443431177466446916319867062128867811451292833717675081551803755143128885524389827706879L

pypol.series.bernstein(v, n)

Returns the Bernstein polynomial

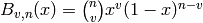
Raises :ValueError if v or n are negative or v is greater than n Return type:pypol.Polynomial

Examples

>>> bernstein(0, 0)
+ 1
>>> bernstein(0, 1)
- x + 1
>>> bernstein(0, 2)
+ x^2 - 2x + 1
>>> bernstein(1, 2)
- 2x^2 + 2x
>>> bernstein(-1, 2)
Traceback (most recent call last):
  File "<pyshell#5>", line 1, in <module>
    bernstein(-1, 2)
  File "series.py", line 897, in bernstein
    raise ValueError('Bernstein polynomials only defined for v >= 0 and n >= 0')
ValueError: Bernstein polynomials only defined for v >= 0 and n >= 0
>>> bernstein(3, 2)
Traceback (most recent call last):
  File "<pyshell#6>", line 1, in <module>
    bernstein(3, 2)
  File "series.py", line 899, in bernstein
    raise ValueError('v cannot be greater than n')
ValueError: v cannot be greater than n
>>> bernstein(3, 6)
- 20x^6 + 60x^5 - 60x^4 + 20x^3
>>> bernstein(13, 16)
- 560x^16 + 1680x^15 - 1680x^14 + 560x^13
>>> bernstein(18, 19)
- 19x^19 + 19x^18

References

MathWorld