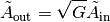Overview¶
Domain¶
A domain in pyofss contains the temporal and spectral axis (arrays) which are used by the system modules during simulation. There are helper functions which convert between frequency, angular frequency, and wavelength.
- TB – total bits
- SPB – samples per bit
- BW – bit width
- TS – total samples (TS = TB x SPB)
- TW – time window (TW = TB x BW)
Using 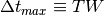 and
and 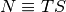 , the temporal
array corresponding to
, the temporal
array corresponding to 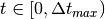 is generated from
is generated from
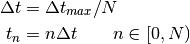
The first and last elements of the temporal array will have the values:
![t[0] &= 0.0 \\
t[N-1] &= \Delta t_{max} - \Delta t](_images/math/bf24147cfd5ddeccd0ec9ece321e07ca99640975.png)
For the spectral array there will be a fixed shift such that the middle of the
array corresponds to a central frequency 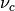 .
Then the spectral array corresponding to
.
Then the spectral array corresponding to
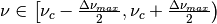 is generated from
is generated from
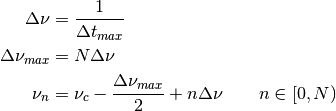
The first and last elements of the spectral array will have the values:
![\nu[0] &= \nu_c - \frac{ \Delta \nu_{max} }{ 2 } \\
\nu[N-1] &= \nu_c + \frac{ \Delta \nu_{max} }{ 2 } - \Delta \nu](_images/math/c04edfdcbd20f5da404b00311a8b66f3f23a781b.png)
An angular frequency array and a wavelength array are also generated using the following two relations
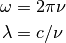
Field¶
The field in pyofss represents the complex valued slowly varying envelope of the electric field that will be propagated through the optical fibre system. A fixed polarisation is used for the field. It is possible to use separate field arrays for each frequency/wavelength (channel) to be simulated.
Modules¶
A module in pyofss is a class that may be called with a domain and a field as parameters. The following modules may be generated:
Gaussian¶
![A(0,t) = \sqrt{P_0} \, \exp \left[ \frac{ -(1+iC) }{ 2 } \left( \
\frac{ t-t_0 }{ \Delta t_{1/e} } \
\right)^{2m} + i \left( \phi_0 - \
2 \pi (\nu_c + \nu_\text{offset})t \
\right) \right]](_images/math/cc9e16ec1ba3752ba5f359881f6ac9fbaa7cb47d.png)
The gaussian module will generate a (super-)Gaussian shaped pulse using the following parameters:
– Peak power (W)
– Chirp parameter (rad)
– pulse position (ps)
– pulse HWIeM width (ps) [note: not FWHM]
– Order paramater
– initial phase (rad)
– centre frequency (THz)
– offset frequency (THz)
Since the centre frequency 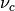 is fixed by the domain, only the
offset frequency
is fixed by the domain, only the
offset frequency 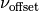 is provided by the user.
is provided by the user.
The pulse position 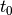 is given as a factor of the time window
is given as a factor of the time window
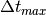 such that
such that 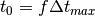 , and the user
supplies the factor
, and the user
supplies the factor 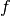 .
.
Sech¶
![A(0,t) = \sqrt{P_0} \, \text{sech} \left( \
\frac{ t-t_0 }{ \Delta t_{1/e} } \right) \
\, \exp \left[ \frac{ -iC }{ 2 } \left( \
\frac{ t-t_0 }{ \Delta t_{1/e} } \
\right)^2 + i \left( \phi_0 - \
2 \pi (\nu_c + \nu_\text{offset}) t \
\right) \right]](_images/math/ad211c05036c31c780a4a00b478471e0dfc41fe1.png)
The sech module will generate a hyperbolic-Secant shaped pulse using the following parameters:
– Peak power (W)
– Chirp parameter (rad)
– pulse position (ps)
– pulse HWIeM width (ps) [note: not FWHM]
– initial phase (rad)
– centre frequency (THz)
– offset frequency (THz)
Since the centre frequency 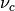 is fixed by the domain, only the
offset frequency
is fixed by the domain, only the
offset frequency 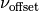 is provided by the user.
is provided by the user.
The pulse position 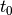 is given as a factor of the time window
is given as a factor of the time window
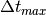 such that
such that 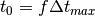 , and the user
supplies the factor
, and the user
supplies the factor 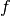 .
.
Generator¶
A generator module can generate Gaussian or hyperbolic-secant (Sech) shaped
pulses.
The main difference to directly calling a Gaussian or Sech module is that the
pulse position paramter 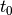 is given as a factor of the bit width, and
not as a factor of the time window.
The user provides the factor
is given as a factor of the bit width, and
not as a factor of the time window.
The user provides the factor 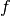 where
where 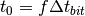 .
.
Fibre¶
The fibre module propagates the input field incrementally using the generalised non-linear Schrödinger equation:
![\frac{ \partial{A} }{ \partial{z} } = \left[ \hat{L} + \
\hat{N}\left(A\right) \right] A](_images/math/42df149fc887a97b35f79a70713f68408827cab5.png)
where 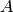 is the complex field envelope of the pulse and
is the complex field envelope of the pulse and  is the
dimension along the fibre length. The linear operator
is the
dimension along the fibre length. The linear operator 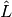 and
non-linear operator
and
non-linear operator 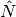 are usually written:
are usually written:
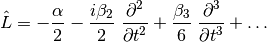
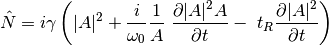
The linear operator contains terms for attenuation and (second order and higher) dispersion. The nonlinear operator contains terms for self-phase modulation (SPM), self-steepening, and Raman scattering.
It is useful to apply the linear operator to the field in the frequency domain
using the property 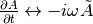 :
:
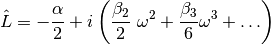
![H(\nu) = \exp \left[ \left(\frac{- 2 \pi \
\nu_\text{filter}}{2 \Delta \nu} \right)^{2m} \right]](_images/math/068e99e64e025fd36075988f91b946734184aa82.png)