Ring¶

This is a simple, but very good, example because it shows how easy is to model circumferences just by aggregation of planar polygons. In this case, I will let the number of these polygons free to be changed whenever we want, what will allow us to set the appropriate balance between accuracy and time execution.

This problem arised to me some time ago when I was discussing with a mate about the radiation effect on the high voltage cables. I like as an example because it clearly shows the pyny3d polyvalence and adaptability to whatever problem that includes the Sun as an important factor to take into account.

In general, the process I have followed to build the ring is just to create a polygon sample, with the sensible points, and rotate copies of it around the ring circle:

import numpy as np
import pyny3d.geoms as pyny

# Input
r = 1  # radius
n_faces = 30  # number of polygons

# Geometry
a = 2*np.pi/n_faces  # rotation angle step
face = pyny.Place(np.array([[0, -r*np.sin(a/2), r*np.cos(a/2)],
                            [0, r*np.sin(a/2), r*np.cos(a/2)],
                            [0.5, r*np.sin(a/2), r*np.cos(a/2)],
                            [0.5, -r*np.sin(a/2), r*np.cos(a/2)]]))
face.mesh(0.03, extra_height=0.01)
rotated_list = []
for rot in np.arange(0, 2*np.pi, a):
    rotated_list.append(face.rotate(rot, 'x', (0,0,0)))
cable = pyny.Space(rotated_list)
## Viz
cable.iplot()

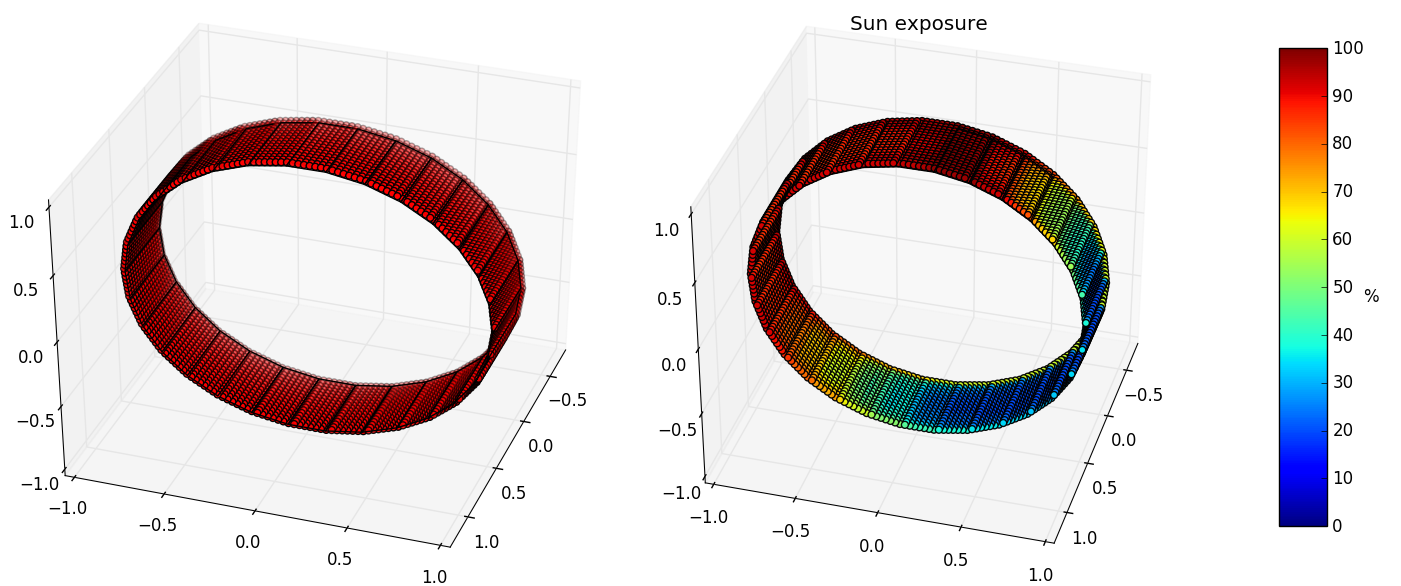
# Irradiation simulation
S = cable.shadows(init='auto', resolution='high')
## Viz
S.viz.exposure_plot(extra_height=0)

Ring created with 30 polygons. It has 3570 points.