solutions Package

analyticsolution Module

analyticsolution.py - Analytic solutions for the second order Klein-Gordon equation

class pyflation.solutions.analyticsolution.AnalyticSolution(*args, **kwargs)

Bases: pyflation.solutions.generalsolution.GeneralSolution

Analytic Solution base class.

full_source_from_model(m, nix, **kwargs)

Use the data from a model at a timestep nix to calculate the full source term S.

class pyflation.solutions.analyticsolution.ImaginaryInverseSolution(*args, **kwargs)

Bases: pyflation.solutions.analyticsolution.AnalyticSolution

Analytic solution using an imaginary inverse solution as the first order solution and with no phase information.

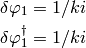
where

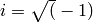
J_A(k, Cterms, **kwargs)

Solution for J_A which is the integral for A in terms of constants C1 and C2.

J_B(k, Cterms, **kwargs)

Solution for J_B which is the integral for B in terms of constants C3 and C4.

J_C(k, Cterms, **kwargs)

Second method for J_C

J_D(k, Cterms, **kwargs)

Solution for J_D which is the integral for D in terms of constants C6 and C7.

J_general_Atype(k, C, n)

J_general_Btype(k, C, n)

class pyflation.solutions.analyticsolution.NoPhaseBunchDaviesSolution(*args, **kwargs)

Bases: pyflation.solutions.analyticsolution.AnalyticSolution

Analytic solution using the Bunch Davies initial conditions as the first order solution and with no phase information.

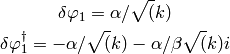
J_A(k, Cterms, **kwargs)

Solution for J_A which is the integral for A in terms of constants C1 and C2.

J_B(k, Cterms, **kwargs)

Solution for J_B which is the integral for B in terms of constants C3 and C4.

J_C(k, Cterms, **kwargs)

Second method for J_C

J_D(k, Cterms, **kwargs)

Solution for J_D which is the integral for D in terms of constants C6 and C7.

calculate_Cterms(bgvars, a, potentials)

Calculate the constant terms needed for source integration.

full_source_from_model(m, nix)

Use the data from a model at a timestep nix to calculate the full source term S.

class pyflation.solutions.analyticsolution.OldSimpleInverseFull(*args, **kwargs)

Bases: pyflation.solutions.analyticsolution.AnalyticSolution

Analytic solution using a simple inverse solution as the first order solution and with no phase information. This uses the solutions of the old equations and is not reliable. Should not be used in production.

deltaarphi_1 = 1/k dN{deltaarphi_1} = 1/k

J_A1(k, Cterms, **kwargs)

Solution for J_A which is the integral for A in terms of constants C1 and C2.

J_A2(k, Cterms, **kwargs)

Solution for J_A which is the integral for A in terms of constants C1 and C2.

J_B1(k, Cterms, **kwargs)

Solution for J_B which is the integral for B in terms of constants C3 and C4.

J_B2(k, Cterms, **kwargs)

Solution for J_B which is the integral for B in terms of constants C3 and C4.

J_C1(k, Cterms, **kwargs)

Second method for J_C

J_C2(k, Cterms, **kwargs)

Second method for J_C

J_D1(k, Cterms, **kwargs)

Solution for J_D which is the integral for D in terms of constants C6 and C7.

J_D2(k, Cterms, **kwargs)

Solution for J_D which is the integral for D in terms of constants C6 and C7.

J_E1(k, Cterms, **kwargs)

Solution for J_D which is the integral for D in terms of constants C6 and C7.

J_E2(k, Cterms, **kwargs)

Solution for J_D which is the integral for D in terms of constants C6 and C7.

J_F1(k, Cterms, **kwargs)

Solution for J_D which is the integral for D in terms of constants C6 and C7.

J_F2(k, Cterms, **kwargs)

Solution for J_D which is the integral for D in terms of constants C6 and C7.

J_G1(k, Cterms, **kwargs)

Solution for J_D which is the integral for D in terms of constants C6 and C7.

J_G2(k, Cterms, **kwargs)

Solution for J_D which is the integral for D in terms of constants C6 and C7.

J_general_Atype(k, C, n)

J_general_Btype(k, C, n)

J_general_Etype(k, C, n)

J_general_Ftype(k, C, n)

class pyflation.solutions.analyticsolution.SimpleInverseFull(*args, **kwargs)

Bases: pyflation.solutions.analyticsolution.AnalyticSolution

Analytic solution using a simple inverse solution as the first order solution and with no phase information.

J_factory(Jkey)

J_general_Atype(k, C, n)

J_general_Btype(k, C, n)

J_general_Etype(k, C, n)

J_general_Ftype(k, C, n)

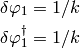
class pyflation.solutions.analyticsolution.SimpleInverseSolution(*args, **kwargs)

Bases: pyflation.solutions.analyticsolution.AnalyticSolution

Analytic solution using a simple inverse solution as the first order solution and with no phase information.

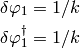
J_A(k, Cterms, **kwargs)

Solution for J_A which is the integral for A in terms of constants C1 and C2.

J_B(k, Cterms, **kwargs)

Solution for J_B which is the integral for B in terms of constants C3 and C4.

J_C(k, Cterms, **kwargs)

Second method for J_C

J_D(k, Cterms, **kwargs)

Solution for J_D which is the integral for D in terms of constants C6 and C7.

J_general_Atype(k, C, n)

J_general_Btype(k, C, n)

calcedsolution Module

calcedsolution.py - Calculated solution for convolution integrals

class pyflation.solutions.calcedsolution.CalcedSolution(*args, **kwargs)

Bases: pyflation.solutions.generalsolution.GeneralSolution

Calculated result using romberg integration.

full_source_from_model(m, nix, **kwargs)

Calculate full source term from model m at timestep nix.

get_dp1()

get_dp1dot()

class pyflation.solutions.calcedsolution.ImaginaryInverseCalced(*args, **kwargs)

Bases: pyflation.solutions.calcedsolution.CalcedSolution

Calced solution using an imaginary inverse as the first order solution and with no phase information.

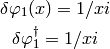
where .

get_dp1(k, **kwargs)

Get dp1 for a certain value of alpha and beta.

get_dp1dot(k, **kwargs)

Get dp1dot for a certain value of alpha and beta.

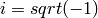class pyflation.solutions.calcedsolution.NoPhaseBunchDaviesCalced(*args, **kwargs)

Bases: pyflation.solutions.calcedsolution.CalcedSolution

Calced solution using the Bunch Davies initial conditions as the first order solution and with no phase information.

full_source_from_model(m, nix)

Calculate full source term from model m at timestep nix.

get_dp1(k, **kwargs)

Get dp1 for a certain value of alpha and beta.

get_dp1dot(k, **kwargs)

Get dp1dot for a certain value of alpha and beta.

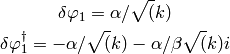
class pyflation.solutions.calcedsolution.SimpleInverseCalced(*args, **kwargs)

Bases: pyflation.solutions.calcedsolution.CalcedSolution

Calced solution using a simple inverse as the first order solution and with no phase information.

get_dp1(k, **kwargs)

Get dp1 for a certain value of alpha and beta.

get_dp1dot(k, **kwargs)

Get dp1dot for a certain value of alpha and beta.

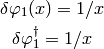
comparison Module

comparison.py - Comparison of analytic and calculated solutions

pyflation.solutions.comparison.compare_J_terms(m, nix, srcclass=None, analytic_class=None, calced_class=None, only_calced_Cterms=False, fx=None)

Compare the analytic and calculated results for each J_term using the results from model m at the timestep nix

pyflation.solutions.comparison.compare_one_step(m, nix, srcclass=None, analytic_class=None, calced_class=None, fx=None)

Compare the analytic and calculated solutions for equations from srclass using the results from m at the timestep nix.

fixtures Module

fixtures.py - Module with fixture information and generating functions

pyflation.solutions.fixtures.fixture_from_model(m, numsoks=None, nthetas=513)

Generate a single fixture from a cosmomodels model.

If numsoks is not specified, then use the last value in the defaults.

pyflation.solutions.fixtures.generate_fixtures(kmins=[1e-61, 3.0000000000000001e-61, 9.9999999999999997e-61], deltaks=[1e-61, 3.0000000000000001e-61, 9.9999999999999997e-61], numsoks=[257, 513, 1025], nthetas=[129, 257, 513])

Generator for fixtures created from cartesian products of input lists.

generalsolution Module

generalsolution.py - Holds the general solution base class

class pyflation.solutions.generalsolution.GeneralSolution(fixture, srcclass)

Bases: object

General solution base class.

full_source_from_model(m, nix)