More Examples

Instability of Natural Extension

Example adapted from [1] (page 443).

Original model:

>>> from improb.lowprev.lowpoly import LowPoly
>>> lpr = LowPoly('abcd', number_type='fraction')
>>> lpr.set_upper([1, '2/3', 0, 2], '1/2')
>>> lpr.set_upper([0, 1, 3, 0], '3/2')
>>> lpr.get_upper([0,2,2,0])
2
>>> list(lpr.get_credal_set())
[(Fraction(1, 2), 0, Fraction(1, 2), 0), (0, Fraction(3, 4), Fraction(1, 4), 0)]

Perturbated model:

>>> lpr = LowPoly('abcd', number_type='fraction')
>>> lpr.set_upper([1, '0.66667', 0, 2], '1/2')
>>> lpr.set_upper([0, 1, 3, 0], '3/2')
>>> lpr.get_upper([0,2,2,0])
1
>>> list(lpr.get_credal_set())
[(Fraction(1, 2), 0, Fraction(1, 2), 0)]

Existence of incurring sure loss perturbation of original model:

>>> lpr = LowPoly('abcd', number_type='fraction')
>>> lpr.set_upper([1, '2/3', 0, 2], '0.49999')
>>> lpr.set_upper([0, 1, 3, 0], '3/2')
>>> lpr.is_avoiding_sure_loss()
False

Small vacuous mixture of the perturbated (still instable) model (alpha is 0.999):

>>> lpr = LowPoly('abcd', number_type='fraction')
>>> lpr.set_upper([1, '0.66667', 0, 2], '0.5015')
>>> lpr.set_upper([0, 1, 3, 0], '1.5015')
>>> lpr.get_upper([0,2,2,0])
2

So vacuous mixture is not stable!

Footnotes

[1]	Stephen M. Robinson. A characterization of stability in linear programming. Operations Research, 25(3):435–447, 1977.

Mobius Transform and Natural Extension

This example shows that, in general, the Mobius transform of a coherent lower probability cannot be used to calculate its natural extension.

>>> import itertools
>>> import random
>>> from improb.lowprev.lowprob import LowProb
>>> from improb.lowprev.belfunc import BelFunc
>>> random.seed(10)
>>> n = 4
>>> events = [list(event) for event in itertools.product([0, 1], repeat=n)]
>>> gambles = [[random.randint(0,2) for i in range(n)] for j in range(20)]
>>> for i in range(20):
...     # construct belief function from lower probability
...     lpr = LowProb.make_random(pspace=n, division=2, number_type='fraction')
...     lpr.extend()
...     bel = BelFunc(lpr)
...     # check for incoherence
...     for gamble in gambles:
...         if lpr.number_cmp(lpr.get_lower(gamble), bel.get_lower(gamble)) != 0:
...             print('lpr (lower probability):')
...             print(lpr)
...             print('bel.mobius (basic belief assignment):')
...             print(bel.mobius)
...             print("lpr.get_lower({0})={1}".format(gamble, lpr.get_lower(gamble)))
...             print("bel.get_lower({0})={1}".format(gamble, bel.get_lower(gamble)))
...             break
...     else:
...         # no incoherence found! try another one
...         continue
...     break
... else:
...     raise RuntimeError("no counterexample found")
lpr (lower probability):
        : 0
0       : 0
  1     : 0
    2   : 0
      3 : 0
0 1     : 0
0   2   : 1/2
0     3 : 1/2
  1 2   : 1/2
  1   3 : 1/2
    2 3 : 0
0 1 2   : 1/2
0 1   3 : 1/2
0   2 3 : 1/2
  1 2 3 : 1/2
0 1 2 3 : 1
bel.mobius (basic belief assignment):
        : 0
0       : 0
  1     : 0
    2   : 0
      3 : 0
0 1     : 0
0   2   : 1/2
0     3 : 1/2
  1 2   : 1/2
  1   3 : 1/2
    2 3 : 0
0 1 2   : -1/2
0 1   3 : -1/2
0   2 3 : -1/2
  1 2 3 : -1/2
0 1 2 3 : 1
lpr.get_lower([2, 0, 1, 1])=1
bel.get_lower([2, 0, 1, 1])=1/2

Quick check:

lpr.get_lower([2,0,1,1]) >= lpr([1,0,1,0])+lpr([1,0,0,1])=1
bel.get_lower([2,0,1,1]) = 0.5*(1+1+0+0+0+0-1+0+0)=0.5

However, the Mobius transform of a 2-monotone lower probability can be used to calculate its natural extension. The following simulation confirms this for a space of size 3 (all coherent lower probabilities on such space are 2-monotone).

>>> import itertools
>>> import random
>>> from improb.lowprev.lowprob import LowProb
>>> from improb.lowprev.belfunc import BelFunc
>>> random.seed(10)
>>> n = 3
>>> gambles = [[random.randint(0,5) for i in range(n)] for j in range(20)]
>>> for i in range(20): # increase at will...
...     # construct a coherent lower probability
...     lpr = LowProb.make_random(pspace=n, division=2, number_type='fraction')
...     lpr.extend()
...     set_function = lpr.set_function
...     mobius = lpr.mobius
...     # check for incoherence
...     for gamble in gambles:
...         if lpr.number_cmp(lpr.get_lower(gamble), mobius.get_bba_choquet(gamble)) != 0 or lpr.number_cmp(lpr.get_lower(gamble), set_function.get_choquet(gamble)) != 0:
...             print('lpr (lower probability):')
...             print(lpr)
...             print('mobius (basic belief assignment):')
...             print(mobius)
...             print("lpr.get_lower({0})={1}".format(gamble, lpr.get_lower(gamble)))
...             print("mobius.get_bba_choquet({0})={1}".format(gamble, mobius.get_bba_choquet(gamble)))
...             print("set_function.get_choquet({0})={1}".format(gamble, set_function.get_choquet(gamble)))
...             break
...     else:
...         # no incoherence found! try another one
...         continue
...     break
... else:
...     raise RuntimeError("no counterexample found") 
Traceback (most recent call last):
    ...
RuntimeError: no counterexample found

Finally, note that the Mobius transform can also be used to calculate the Choquet integral with respect to an arbitrary set function for which :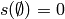

>>> import itertools
>>> import random
>>> from improb import PSpace
>>> from improb.setfunction import SetFunction
>>> random.seed(10)
>>> n = 5
>>> gambles = [[random.randint(-5,5) for i in range(n)] for j in range(20)]
>>> for i in range(20): # increase at will...
...     # construct a random set function
...     pspace = PSpace(n)
...     s = SetFunction(
...         pspace=pspace,
...         data=dict((event, random.randint(-len(pspace), len(pspace)))
...                   for event in pspace.subsets()),
...         number_type='fraction')
...     s[False] = 0
...     m = SetFunction(
...         pspace=pspace,
...         data=dict((event, s.get_mobius(event))
...                   for event in pspace.subsets()),
...         number_type='fraction')
...     # check equality of two types of integrals
...     for gamble in gambles:
...         if s.number_cmp(s.get_choquet(gamble), m.get_bba_choquet(gamble)) != 0:
...             print('s:')
...             print(s)
...             print('m (basic belief assignment):')
...             print(m)
...             print("s.get_choquet({0})={1}".format(gamble, s.get_choquet(gamble)))
...             print("m.get_bba_choquet({0})={1}".format(gamble, m.get_bba_choquet(gamble)))
...             break
...     else:
...         # no inequality! try another one
...         continue
...     break
... else:
...     raise RuntimeError("no counterexample found") 
Traceback (most recent call last):
    ...
RuntimeError: no counterexample found

A Simple Subtree Imperfect Decision Tree

>>> from fractions import Fraction
>>> import itertools
>>> import random
>>> from improb.lowprev.linvac import LinVac
>>> from improb.decision.opt import OptLowPrevMax
>>> random.seed(40)
>>> n1 = 2
>>> n2 = 2
>>> ndec = 3
>>> pspace = [tuple(omega)
...           for omega in itertools.product(list(range(n1)), list(range(n2)))]
>>> for i in range(20):
...     # construct a linear vacuous mixture
...     lprob = [0.8 / len(pspace) for omega in pspace]
...     lpr = LinVac(pspace, lprob=lprob) # no need for randomness
...     opt = OptLowPrevMax(lpr)
...     # construct gambles:
...     # gambles[w1][d][w2] gives the gain of the w1-d-w2 path
...     gambles = [[[random.randint(0, 2) + 0.01 * d + w1 * 0.005
...                  for w2 in range(n2)]
...                 for d in range(ndec)]
...                for w1 in range(n1)]
...     # construct strategies:
...     # strats[i][w1] gives decision of i'th strategy, after observing w1
...     strats = [tuple(strat)
...               for strat in itertools.product(list(range(ndec)), repeat=n1)]
...     # construct normal form gambles:
...     # normgambles[strat][omega] gives the gain of the i'th strategy
...     normgambles = dict(
...         (strat, dict(
...             (omega, gambles[omega[0]][strat[omega[0]]][omega[1]])
...             for omega in pspace))
...         for strat in strats)
...     # construct extensive form gambles:
...     # extgambles[w1][d][omega] gives the gain of decision d after observing w1, as a function of omega
...     extgambles = [[dict((omega, gambles[w1][d][omega[1]] if omega[0] == w1 else 0)
...                         for omega in pspace)
...                    for d in range(ndec)]
...                   for w1 in range(n1)]
...     #print(gambles)
...     #print(strats)
...     #print([[normgambles[strat][omega] for omega in pspace] for strat in strats])
...     #print([[[extgambles[w1][d][omega] for omega in pspace] for d in range(ndec)] for w1 in range(n1)])
...     # calculate normal form solution of subtrees after observing w1
...     local = {}
...     for w1 in range(n1):
...         event = set(w for w in pspace if w[0] == w1)
...         local[w1] = list(opt([extgambles[w1][d] for d in range(ndec)], event))
...         #print(w1, event)
...         #print(local[w1])
...     # calculate full solution by combining all local solutions
...     normlocal = set()
...     for localgambles in itertools.product(*[local[w1] for w1 in range(n1)]):
...         #print localgambles
...         normlocal.add(tuple(sum(localgamble[w] for localgamble in localgambles) for w in pspace))
...     #print(normlocal)
...     # calculate full normal form solution
...     norm = opt([normgambles[strat] for strat in strats])
...     norm = set(tuple(normgamble[w] for w in pspace) for normgamble in norm)
...     #print(norm)
...     # calculate corresponding strategies
...     localstrats = set()
...     normstrats = set()
...     for strat in strats:
...         normgamble = tuple(normgambles[strat][omega] for omega in pspace)
...         if normgamble in norm:
...             normstrats.add(strat)
...         if normgamble in normlocal:
...             localstrats.add(strat)
...     # convert normal form to extensive form
...     normstrats2 = set(itertools.product(*[set(strat[w1] for strat in normstrats) for w1 in range(n1)]))
...     # check if solutions differ
...     if localstrats != normstrats:
...         for w1 in range(n1):
...             for d in range(ndec):
...                 print(
...                     "w1={0}, d={1}: ".format(w1, d)
...                     + " ".join("{0:.3f}".format(x) for x in gambles[w1][d]))
...         print("lpr=" + " ".join(str(x) for x in lprob))
...         print(sorted(normstrats))
...         print(sorted(localstrats))
...         #print(sorted(localstrats - normstrats))
...         #print(sorted(normstrats - localstrats)) # should be empty!
...         #print(sorted(normstrats2))
...         break
...     # stronger violation... never occurs??
...     #if localstrats != normstrats2:
... else:
...     raise RuntimeError("no counterexample found")
w1=0, d=0: 1.000 2.000
w1=0, d=1: 0.010 0.010
w1=0, d=2: 2.020 1.020
w1=1, d=0: 0.005 1.005
w1=1, d=1: 2.015 1.015
w1=1, d=2: 0.025 2.025
lpr=0.2 0.2 0.2 0.2
[(0, 1), (2, 1), (2, 2)]
[(0, 1), (0, 2), (2, 1), (2, 2)]

Stronger Violation of Subtree Perfectness

Does subtree imperfectness persists after converting the normal form into an extensive form?

>>> import itertools
>>> import random
>>> from improb.lowprev.lowprob import LowProb
>>> from improb.decision.opt import OptLowPrevMax
>>> random.seed(10)
>>> n1 = 2
>>> n2 = 3
>>> ndec = 3
>>> pspace = [tuple(omega)
...           for omega in itertools.product(list(range(n1)), list(range(n2)))]
>>> for i in range(20):
...     # construct a lower prevision
...     lpr = LowProb.make_random(pspace=pspace, zero=False)
...     opt = OptLowPrevMax(lpr)
...     # construct gambles:
...     # gambles[w1][d][w2] gives the gain of the w1-d-w2 path
...     gambles = [[[random.randint(0, 5) for w2 in range(n2)]
...                 for d in range(ndec)]
...                for w1 in range(n1)]
...     # construct strategies:
...     # strats[i][w1] gives decision of i'th strategy, after observing w1
...     strats = [tuple(strat)
...               for strat in itertools.product(list(range(ndec)), repeat=n1)]
...     # construct normal form gambles:
...     # normgambles[strat][omega] gives the gain of the i'th strategy
...     normgambles = dict(
...         (strat, dict(
...             (omega, gambles[omega[0]][strat[omega[0]]][omega[1]])
...             for omega in pspace))
...         for strat in strats)
...     # construct extensive form gambles:
...     # extgambles[w1][d][omega] gives the gain of decision d after observing w1, as a function of omega
...     extgambles = [[dict((omega, gambles[w1][d][omega[1]] if omega[0] == w1 else 0)
...                         for omega in pspace)
...                    for d in range(ndec)]
...                   for w1 in range(n1)]
...     #print(gambles)
...     #print(strats)
...     #print([[normgambles[strat][omega] for omega in pspace] for strat in strats])
...     #print([[[extgambles[w1][d][omega] for omega in pspace] for d in range(ndec)] for w1 in range(n1)])
...     # calculate normal form solution of subtrees after observing w1
...     local = {}
...     for w1 in range(n1):
...         event = set(w for w in pspace if w[0] == w1)
...         local[w1] = list(opt([extgambles[w1][d] for d in range(ndec)], event))
...         #print(w1, event)
...         #print(local[w1])
...     # calculate full solution by combining all local solutions
...     normlocal = set()
...     for localgambles in itertools.product(*[local[w1] for w1 in range(n1)]):
...         #print localgambles
...         normlocal.add(tuple(sum(localgamble[w] for localgamble in localgambles) for w in pspace))
...     #print(normlocal)
...     # calculate full normal form solution
...     norm = opt([normgambles[strat] for strat in strats])
...     norm = set(tuple(normgamble[w] for w in pspace) for normgamble in norm)
...     #print(norm)
...     # calculate corresponding strategies
...     localstrats = set()
...     normstrats = set()
...     for strat in strats:
...         normgamble = tuple(normgambles[strat][omega] for omega in pspace)
...         if normgamble in norm:
...             normstrats.add(strat)
...         if normgamble in normlocal:
...             localstrats.add(strat)
...     # convert normal form to extensive form
...     normstrats2 = set(itertools.product(*[set(strat[w1] for strat in normstrats) for w1 in range(n1)]))
...     # check if solutions differ
...     # stronger violation!!
...     if localstrats != normstrats2:
...         for w1 in range(n1):
...             for d in range(ndec):
...                 print(
...                     "w1={0}, d={1}: ".format(w1, d)
...                     + " ".join("{0:.2f}".format(x) for x in gambles[w1][d]))
...         for (gamble, event), (lprev, uprev) in lpr.iteritems():
...             print("lpr({0})={1:.2f}".format(gamble, lprev))
...         print(sorted(normstrats2))
...         print(sorted(localstrats))
...         break
... else:
...     raise RuntimeError("no counterexample found") 
Traceback (most recent call last):
    ...
RuntimeError: no counterexample found