Probability Measures

class improb.lowprev.prob.Prob(pspace=None, mapping=None, lprev=None, uprev=None, prev=None, lprob=None, uprob=None, prob=None, bba=None, credalset=None, number_type=None)

Bases: improb.lowprev.linvac.LinVac

A probability measure, implemented as a LinVac whose natural extension is calculated via expectation; see get_precise().

>>> p = Prob(5, prob=['0.1', '0.2', '0.3', '0.05', '0.35'])
>>> print(p)
0 : 1/10
1 : 1/5
2 : 3/10
3 : 1/20
4 : 7/20
>>> print(p.get_precise([2, 4, 3, 8, 1]))
53/20
>>> print(p.get_precise([2, 4, 3, 8, 1], [0, 1]))
10/3

>>> p = Prob(3, prob={(0,): '0.4'})
>>> print(p)
0 : 2/5
1 : undefined
2 : undefined
>>> p.extend()
>>> print(p)
0 : 2/5
1 : 3/10
2 : 3/10

get_linvac(epsilon)

Convert probability into a linear vacuous mixture:

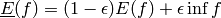
get_precise(gamble, event=True, algorithm='linear')

Calculate the conditional expectation,

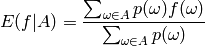
where 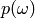is simply the probability of the singleton :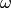

self[{omega: 1}, True][0]

classmethod make_random(pspace=None, division=None, zero=True, number_type='float')

Generate a random probability mass function.

>>> import random
>>> random.seed(25)
>>> print(Prob.make_random("abcd", division=10))
a : 0.4
b : 0.0
c : 0.1
d : 0.5
>>> random.seed(25)
>>> print(Prob.make_random("abcd", division=10, zero=False))
a : 0.3
b : 0.1
c : 0.2
d : 0.4