Graph graphx_pagerank¶

graphx_pagerank(self, output_property, input_edge_labels=None, max_iterations=None, reset_probability=None, convergence_tolerance=None)¶

Determine which vertices are the most important.

Parameters:

Parameters:	output_property : unicode Name of the property to which PageRank value will be stored on vertex and edge. input_edge_labels : list (default=None) List of edge labels to consider for PageRank computation. Default is all edges are considered. max_iterations : int32 (default=None) The maximum number of iterations that will be invoked. The valid range is all positive int. Invalid value will terminate with vertex page rank set to reset_probability. Default is 20. reset_probability : float64 (default=None) The probability that the random walk of a page is reset. Default is 0.15. convergence_tolerance : float64 (default=None) The amount of change in cost function that will be tolerated at convergence. If this parameter is specified, max_iterations is not considered as a stopping condition. If the change is less than this threshold, the algorithm exits earlier. The valid value range is all float and zero. Default is 0.001.
Returns:	: dict dict((vertex_dictionary, (label, Frame)), (edge_dictionary,(label,Frame))). Dictionary containing dictionaries of labeled vertices and labeled edges. For the vertex_dictionary the vertex type is the key and the corresponding vertex’s frame with a new column storing the page rank value for the vertex. Call vertex_dictionary[‘label’] to get the handle to frame whose vertex type is label. For the edge_dictionary the edge type is the key and the corresponding edge’s frame with a new column storing the page rank value for the edge. Call edge_dictionary[‘label’] to get the handle to frame whose edge type is label.

output_property : unicode

Name of the property to which PageRank value will be stored on vertex and edge.

input_edge_labels : list (default=None)

List of edge labels to consider for PageRank computation. Default is all edges are considered.

max_iterations : int32 (default=None)

The maximum number of iterations that will be invoked. The valid range is all positive int. Invalid value will terminate with vertex page rank set to reset_probability. Default is 20.

reset_probability : float64 (default=None)

The probability that the random walk of a page is reset. Default is 0.15.

convergence_tolerance : float64 (default=None)

The amount of change in cost function that will be tolerated at convergence. If this parameter is specified, max_iterations is not considered as a stopping condition. If the change is less than this threshold, the algorithm exits earlier. The valid value range is all float and zero. Default is 0.001.

Returns:

: dict

dict((vertex_dictionary, (label, Frame)), (edge_dictionary,(label,Frame))).

Dictionary containing dictionaries of labeled vertices and labeled edges.

For the vertex_dictionary the vertex type is the key and the corresponding vertex’s frame with a new column storing the page rank value for the vertex. Call vertex_dictionary[‘label’] to get the handle to frame whose vertex type is label.

For the edge_dictionary the edge type is the key and the corresponding edge’s frame with a new column storing the page rank value for the edge. Call edge_dictionary[‘label’] to get the handle to frame whose edge type is label.

Pulls graph from underlying store, sends it off to the PageRankRunner, and then writes the output graph back to the underlying store.

** Experimental Feature **

Basics and Background

PageRank is a method for determining which vertices in a directed graph are the most central or important. PageRank gives each vertex a score which can be interpreted as the probability that a person randomly walking along the edges of the graph will visit that vertex.

The calculation of PageRank is based on the supposition that if a vertex has many vertices pointing to it, then it is “important”, and that a vertex grows in importance as more important vertices point to it. The calculation is based only on the network structure of the graph and makes no use of any side data, properties, user-provided scores or similar non-topological information.

PageRank was most famously used as the core of the Google search engine for many years, but as a general measure of centrality in a graph, it has other uses to other problems, such as recommendation systems and analyzing predator-prey food webs to predict extinctions.

Background references

Basic description and principles: Wikipedia: PageRank
Applications to food web analysis: Stanford: Applications of PageRank
Applications to recommendation systems: PLoS: Computational Biology

Mathematical Details of PageRank Implementation

The Trusted Analytics Platform implementation of PageRank satisfies the following equation at each vertex $v$ of the graph:

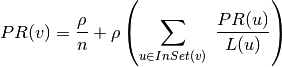
$PR(v) = \frac {\rho}{n} + \rho \left( \sum_{u\in InSet(v)} \ \frac {PR(u)}{L(u)} \right)$

Where:: $v$ — a vertex

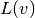$L(v)$ — outbound degree of the vertex v

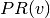$PR(v)$ — PageRank score of the vertex v

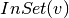$InSet(v)$ — set of vertices pointing to the vertex v

$n$ — total number of vertices in the graph

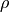$\rho$ — user specified damping factor (also known as reset probability)

Termination is guaranteed by two mechanisms.

The user can specify a convergence threshold so that the algorithm will terminate when, at every vertex, the difference between successive approximations to the PageRank score falls below the convergence threshold.
The user can specify a maximum number of iterations after which the algorithm will terminate.

Examples

>>> graph = ta.Graph()

>>> graph.define_vertex_type('source')
[===Job Progress===]
>>> graph.vertices['source'].add_vertices(vertex_frame, 'source', 'label')
[===Job Progress===]
>>> graph.define_edge_type('edges','source', 'source', directed=False)
[===Job Progress===]
>>> graph.edges['edges'].add_edges(edge_frame, 'source', 'dest', ['weight'])
[===Job Progress===]
>>> result = graph.graphx_pagerank(output_property="PageRank",max_iterations=2,convergence_tolerance=0.001)
[===Job Progress===]
>>> graph.edges['edges'].inspect()
    [#]  _eid  _src_vid  _dest_vid  _label  weight
    ==============================================
    [0]     6         1          2  edges        1
    [1]     7         1          3  edges        1
    [2]     9         1          4  edges        1
    [3]     8         2          3  edges        1
    [4]    10         4          5  edges        1
>>> result['edge_dictionary']['edges'].row_count
10
>>> result['vertex_dictionary']['source'].row_count
5

Quick search

Table Of Contents

Graph graphx_pagerank¶