seapy.couplings.couplingsurfaceacoustical.tau¶
- seapy.couplings.couplingsurfaceacoustical.tau(f, fc, rho_0, rho_s, c_0, S, U=0.0)[source]¶
Non-resonant transmission coefficient by Leppington et al (1987).
Parameters: - f – Frequency
- fc – Critical frequency
- rho_0 – Density air
- rho_s – Density plate
- c_0 – Speed of sound in air
- S – Surface
- U – Shape function
![\tau = \left( \frac{\rho_0 c_0}{\pi f \rho_s \left(1-f^2/f_c^2 \right)} \right)^2 \left( \ln{\left[ \frac{2 \pi f \sqrt{S}}{c_0} \right]} + 0.160 + U(l_x,l_y) + \frac{1}{4 \mu^6} \left[(2\mu^2-1)(\mu^2+1)^2\ln{\left(\mu^2-1\right)} + (2\mu^2+1)(\mu^2-1)^2 \ln{\left(\mu^2+1\right)} - 4\mu^2 - 8\mu^6 \ln{\mu} \right] \right)](../../_images/math/a194e5e3272cf71f2ba45475ebedf230b3d0f8dd.png)
See Craik, equation 4.22, page 101.
Note
The shape function
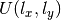is assumed to be zero.Note
The term B3*(C1 + C2 + C3) (see source) can be ignored except close to the critical frequency. We will nevertheless calculate them, and in case they become nan we replace the factor with zero.