Gaussian Process Regression

A simulation is seen as a function $f(x)+\epsilon$ ($x \in \mathbb{R}^D$) with additional random error $\epsilon \sim \mathcal{N}(0,v_t)$. This optional error is due to the stochastic nature of most simulations.

Note

This error does not depend on $x$. An extension to model an error depending on $x$ will be added in the future.

The GaussianProcess module uses regression to model the simulation as a Gaussian process. We refer to Girard’s thesis [1] for a really good explanation of GP regression.

“A Gaussian process is a collection of random variables, any finite number of which have (consistent) joint Gaussian distributions.” – Rasmussen, C. E. Gaussian Processes in Machine Learning, Advanced Lectures on Machine Learning, Springer Berlin Heidelberg, 2004, 3176, 63-71

“Once the mean and covariance functions are defined, everything else about GPs follows from the basic rules of probability applied to multivariate Gaussians.” – Zoubin Ghahramani

Note

The following explanation is an excerpt from my paper [2].

$m(x) = E[G(x)]$ ($x\in\mathbb{R}^d$) is the mean function of the Gaussian process and $C(x_i,x_j) = \mathrm{Cov}[G(x_i),G(x_j)]$ is the covariance function. For any given set of inputs $\{x_1,\dots,x_n\}$, $(G(x_1),\dots,G(x_n))$ is a random vector with an $n$-dimensional normal distribution $\mathcal{N}({\mu},\Sigma)$. ${\mu}$ is the vector of mean values $(m(x_1),\dots,m(x_n))$ and $\Sigma$ is the covariance matrix with $\Sigma_{ij} = C(x_i,x_j)$

For modeling $f(x)$, we use the Gaussian squared exponential covariance function $C(x_i,x_j) = v \exp \left[-\tfrac{1}{2}(x_i-x_j)^T {W}^{-1}(x_i-x_j)\right]$, as it performs well regarding accuracy. Without loss of generality, we use $m(x)=m$.

${W}^{-1} = \mathrm{diag}(w_1,\dots,w_d)$ and $v$ are hyperparameters of the Gaussian process. We have a set of observed simulation results $\mathcal{B} = \{(x_i,t_i)\}_{i=1}^N$ as supporting points with $x_i \in \mathbb{R}^d$ and $t_i = f(x_i)+\epsilon_i$ with white noise $\epsilon_i \sim \mathcal{N}(0,v_t)$. This noise represents the aleatory uncertainty of the simulation that calculates $f(x)$.

To model the noisy observations $t_i$ we use $K=\Sigma + v_t I$ as covariance matrix for regression. Therefore, we have an additional hyperparameter $v_t$. The hyperparameters $W^{-1}$, $v_t$, and $v$ can be estimated from a given dataset with a maximum likelihood approach. In the following, we use ${\beta}={K}^{-1}{t}$ with ${t} = (t_1,\dots,t_N)^T$ to simplify notation.

Now, the Gaussian process can be used as a surrogate for the simulation model. The prediction $\mu(x)$ and code plus aleatory uncertainty $\sigma^2 (x)$ at a new input $x$ is:

$$\begin{split}\mu (x) &= \sum_{i=1}^N \beta_i C(x,x_i) \\ \sigma^2 (x) &= C(x,x) - \sum_{i,j=1}^N K_{ij}^{-1}C(x,x_i)C(x,x_j) + v_t\end{split}$$

1-d Example:

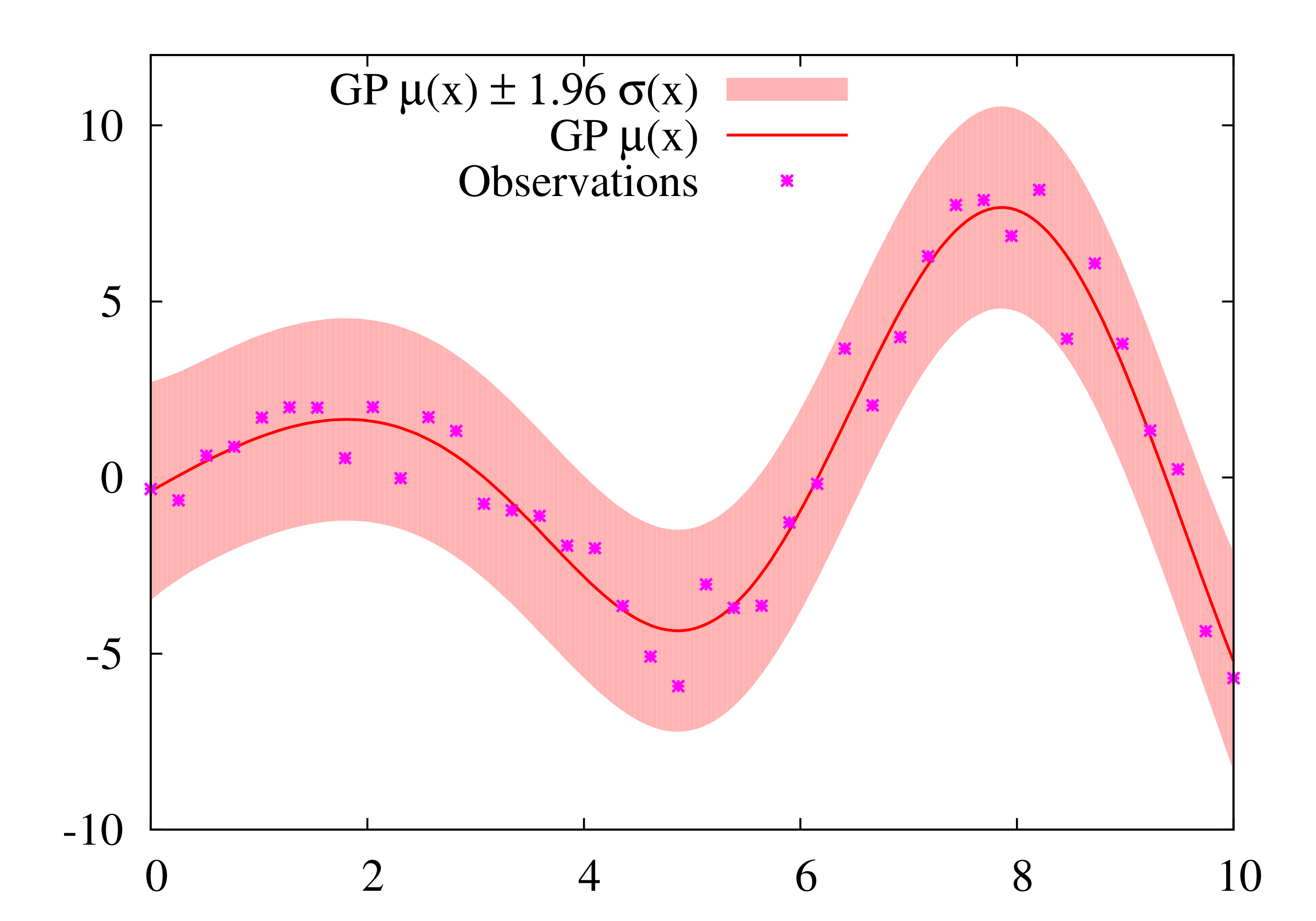
Usage: See Getting Started

References

[1]	Girard, A. Approximate Methods for Propagation of Uncertainty with Gaussian Process Models, University of Glasgow, 2004

[2]	Baumgaertel, P.; Endler, G.; Wahl, A. M. & Lenz, R. Inverse Uncertainty Propagation for Demand Driven Data Acquisition, Proceedings of the 2014 Winter Simulation Conference, IEEE Press, 2014, 710-721 (https://www6.cs.fau.de/publications/public/2014/WinterSim2014_baumgaertel.pdf)