Angle functions¶

Note

These functions deal with vector and matrices manipulations by SOFA. Most of them can be implemented by the user in a perhaps more straightforward and fastest way by directly using math or numpy methods, but they are however implemented and listed here for completeness.

pysofa.a2af(ndp, angle)¶

Decompose radians into degrees, arcminutes, arcseconds, fraction.

Parameters:	ndp (int) – the requested resolution. angle (float) – the value to decompose.
Returns:	a tuple whose first member is a string containing the sign, and the second member is itself a tuple (degrees, arcminutes, arcseconds, fraction).

See also

SOFA manual.pdf page 19

pysofa.a2tf(ndp, angle)¶

Decompose radians into hours, arcminutes, arcseconds, fraction.

Parameters:	ndp (int) – the requested resolution. angle (float) – the value to decompose.
Returns:	a tuple whose first member is a string containing the sign, and the second member is itself a tuple (hours, arcminutes, arcseconds, fraction).

See also

SOFA manual.pdf page 20

pysofa.af2a(s, ideg, iamin, asec)¶

Convert degrees, arcminutes, arcseconds to radians.

Parameters:	s – sign, ‘-‘ for negative, otherwise positive. ideg (int) – degrees. iamin (int) – arcminutes. asec (float) – arcseconds.
Returns:	the converted value in radians as a float.

A UserWarning may be issued in case ideg, iamin or asec: values are outside the range 0-359, 0-59 or 0-59.999...

See also

SOFA manual.pdf page 21

pysofa.anp(a)¶

Normalize a into the range 0 <= result < 2pi.

Parameter:	a (float) – the value to normalize.
Returns:	the normalized value as a float.

See also

SOFA manual.pdf page 22

pysofa.anpm(a)¶

Normalize a into the range -pi <= result < +pi.

Parameter:	a (float) – the value to normalize.
Returns:	the normalized value as a float.

See also

SOFA manual.pdf page 23

pysofa.c2s(p)¶

P-vector to spherical coordinates.

Parameter:

p (numpy.ndarray, matrix or nested sequences of shape (1,3)) – p-vector

Returns:

a tuple of two items:

the longitude angle in radians (float)
the latitude angle in radians (float)

See also

SOFA manual.pdf page 39

pysofa.cp(p)¶

Copy a p-vector.

Parameter:	p (array-like of shape (1,3)) – p-vector to copy.
Returns:	a copy of p as a numpy.matrix of shape 1x3.

See also

SOFA manual.pdf page 53

pysofa.cpv(pv)¶

Copy a pv-vector.

Parameter:	pv (array-like of shape (2,3)) – pv-vector to copy.
Returns:	a copy of pv as a numpy.matrix of shape 2x3.

See also

SOFA manual.pdf page 54

pysofa.cr(r)¶

Copy a rotation matrix.

Parameter:	r (array-like of shape (3,3)) – rotation matrix to copy.
Returns:	a copy of r as a numpy.matrix of shape 3x3.

See also

SOFA manual.pdf page 55

pysofa.d2tf(ndp, days)¶

Decompose days into hours, minutes, seconds, fraction.

Parameters:

ndp (int) – the requested resolution.
days (float) – the value to decompose.

Returns:

a tuple of two items:

the sign as a string (‘+’ or ‘-‘)
a tuple (hours, minutes, seconds, fraction).

See also

SOFA manual.pdf page 58

pysofa.ir()¶

Create a new rotation matrix initialized to the identity matrix.

Returns:	an identity matrix as a numpy.matrix of shape 3x3.

See also

SOFA manual.pdf page 122

pysofa.p2pv(p)¶

Extend a p-vector to a pv-vector by appending a zero velocity.

Parameter:	p (array-like of shape (1,3)) – p-vector to extend.
Returns:	pv-vector as a numpy.matrix of shape 2x3.

See also

SOFA manual.pdf page 142

pysofa.p2s(p)¶

P-vector to spherical polar coordinates.

Parameter:

p (array-like of shape (1,3)) – the p-vector

Returns:

a 3-tuple:

longitude angle in radians (float)
latitude angle in radians (float)
radial distance (float).

See also

SOFA manual.pdf page 143

pysofa.pap(a, b)¶

Position-angle from two p-vectors.

Parameters:	a (array-like of shape (1,3)) – direction of the reference point. b (array-like of shape (1,3)) – direction of point whose position angle is required.
Returns:	position angle of b with respect to a in radians (float).

See also

SOFA manual.pdf page 144

pysofa.pas(al, ap, bl, bp)¶

Postion-angle from spherical coordinates.

Parameters:	al (float) – longitude of point A in radians. ap (float) – latitude of point A in radians. bl (float) – longitude of point B in radians. bp (float) – latitude of point B in radians.
Returns:	position angle of B with respect to A in radians (float).

See also

SOFA manual.pdf page 145

pysofa.pdp(a, b)¶

P-vector inner product.

Parameters:	a (array-like of shape (1,3)) – first p-vector. b (array-like of shape (1,3)) – second p-vector.
Returns:	a dot b as a numpy.matrix of shape 1x3.

See also

SOFA manual.pdf page 147

pysofa.pm(p)¶

Modulus of p-vector.

Parameter:	p (array-like of shape (1,3)) – p-vector.
Returns:	modulus (float).

See also

SOFA manual.pdf page 153

pysofa.pmp(a, b)¶

P-vector subtraction.

Parameters:	a (array-like of shape (1,3)) – first p-vector. b (array-like of shape (1,3)) – second p-vector.
Returns:	a - b as a numpy.matrix of shape 1x3.

See also

SOFA manual.pdf page 158

pysofa.pn(p)¶

Convert a p-vector into modulus and unit vector.

Parameter:

p (array-like of shape (1,3)) – p-vector.

Returns:

2-tuple:

the modulus (float)
unit vector (numpy.matrix of shape 1x3)

See also

SOFA manual.pdf page 159

pysofa.ppp(a, b)¶

P-vector addition.

Parameters:	a (array-like of shape (1,3)) – first p-vector. b (array-like of shape (1,3)) – second p-vector.
Returns:	a + b as a numpy.matrix of shape 1x3.

See also

SOFA manual.pdf page 175

pysofa.ppsp(a, s, b)¶

P-vector plus scaled p-vector.

Parameters:	a (array-like of shape (1,3)) – first p-vector. s (float) – scalar (multiplier for b). b (array-like of shape (1,3)) – second p-vector.
Returns:	a + s*b as a numpy.matrix of shape 1x3.

See also

SOFA manual.pdf page 176

pysofa.pv2p(pv)¶

Discard velocity component of a pv-vector.

Parameter:	pv (array-like of shape (2,3)) – pv-vector.
Returns:	p-vector as a numpy.matrix of shape 1x3.

See also

SOFA manual.pdf page 181

pysofa.pv2s(pv)¶

Convert position/velocity from cartesian to spherical coordinates.

Parameter:

pv (array-like of shape (2,3)) – pv-vector.

Returns:

a 6-tuple:

longitude angle 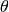$\theta$ in radians (float)
latitude angle 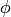$\phi$ in radians (float)
radial distance r (float)
rate of change of 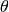$\theta$ (float)
rate of change of 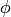$\phi$ (float)
rate of change of r (float)

See also

SOFA manual.pdf page 182

pysofa.pvdpv(a, b)¶

Inner product of two pv-vectors.

Parameters:	a (array-like of shape (2,3)) – first pv-vector. b (array-like of shape (2,3)) – second pv-vector.
Returns:	a . b as a numpy.matrix of shape 1x2.

See also

SOFA manual.pdf page 183

pysofa.pvm(pv)¶

Modulus of pv-vector.

Parameter:

pv (array-like of shape (2,3)) – pv-vector.

Returns:

a 2-tuple:

modulus of position component (float)
modulus of velocity component (float).

See also

SOFA manual.pdf page 184

pysofa.pvmpv(a, b)¶

Subtract one pv-vector from another.

Parameters:	a (array-like of shape (2,3)) – first pv-vector. b (array-like of shape (2,3)) – second pv-vector.
Returns:	a - b as a numpy.matrix of shape 2x3.

See also

SOFA manual.pdf page 185

pysofa.pvppv(a, b)¶

Add one pv-vector to another.

Parameters:	a (array-like of shape (2,3)) – first pv-vector. b (array-like of shape (2,3)) – second pv-vector.
Returns:	a + b as a numpy.matrix of shape 2x3.

See also

SOFA manual.pdf page 186

pysofa.pvu(dt, pv)¶

Update a pv-vector.

Parameters:	dt (float) – time interval. pv (array-like of shape (2,3)) – pv-vector.
Returns:	a new pv-vector as a numpy.matrix of shape 2x3, with p updated and v unchanged.

See also

SOFA manual.pdf page 189

pysofa.pvup(dt, pv)¶

Update a pv-vector, discarding the velocity component.

Parameters:	dt (float) – time interval. pv (array-like of shape (2,3)) – pv-vector.
Returns:	a new p-vector, as a numpy.matrix of shape 1x3.

See also

SOFA manual.pdf page 190

pysofa.pvxpv(a, b)¶

Outer product of two pv-vectors.

Parameters:	a (array-like of shape (2,3)) – first pv-vector. b (array-like of shape (2,3)) – second pv-vector.
Returns:	a x b as a numpy.matrix of shape 2x3.

See also

SOFA manual.pdf page 191

pysofa.pxp(a, b)¶

P-vector outer product.

Parameters:	a (array-like of shape (1,3)) – first p-vector. b (array-like of shape (1,3)) – second p-vector.
Returns:	a x b as a numpy.matrix of shape 1x3.

See also

SOFA manual.pdf page 192

pysofa.rm2v(r)¶

Express a r-matrix as a r-vector.

Parameter:	r (array-like of shape (3,3)) – rotation matrix.
Returns:	rotation vector as a numpy.matrix of shape 1x3.

See also

SOFA manual.pdf page 193

pysofa.rv2m(w)¶

Form the rotation matrix corresponding to a given r-vector.

Parameter:	w (array-like of shape (1,3)) – rotation vector.
Returns:	rotation matrix as a numpy.matrix of shape 3x3.

See also

SOFA manual.pdf page 194

pysofa.rx(phi, r)¶

Rotate a r-matrix about the x-axis.

Parameters:	phi (float) – angle in radians. r (array-like of shape (3,3)) – rotation matrix.
Returns:	the new rotation matrix, as a numpy.matrix of shape 3x3.

See also

SOFA manual.pdf page 195

pysofa.rxp(r, p)¶

Multiply a p-vector by a r-matrix.

Parameters:	r (array-like of shape (3,3)) – rotation matrix. p (array-like of shape (1,3)) – p-vector.
Returns:	r * p as a numpy.matrix of shape 1x3.

See also

SOFA manual.pdf page 196

pysofa.rxpv(r, pv)¶

Multiply a pv-vector by a r-matrix.

Parameters:	r (array-like of shape (3,3)) – rotation matrix. pv (array-like of shape (2,3)) – pv-vector.
Returns:	r * pv as a numpy.matrix of shape 2x3.

See also

SOFA manual.pdf page 197

pysofa.rxr(a, b)¶

Multiply two rotation matrices.

Parameters:	a (array-like of shape (3,3)) – first r-matrix. b (array-like of shape (3,3)) – second r-matrix.
Returns:	a * b as a numpy.matrix of shape 3x3.

See also

SOFA manual.pdf page 198

pysofa.ry(theta, r)¶

Rotate a r-matrix about the y-axis.

Parameters:	theta (float) – angle in radians. r (array-like of shape (3,3)) – rotation matrix.
Returns:	the new rotation matrix, as a numpy.matrix of shape 3x3.

See also

SOFA manual.pdf page 199

pysofa.rz(psi, r)¶

Rotate a r-matrix about the z-axis.

Parameters:	psi (float) – angle in radians. r (array-like of shape (3,3)) – rotation matrix.
Returns:	the new rotation matrix, as a numpy.matrix of shape 3x3.

See also

SOFA manual.pdf page 200

pysofa.s2c(theta, phi)¶

Convert spherical coordinates to cartesian.

Parameters:	theta (float) – longitude angle in radians. phi (float) – latitude angle in radians.
Returns:	direction cosines as a numpy.matrix of shape 1x3.

See also

SOFA manual.pdf page 211

pysofa.s2p(theta, phi, r)¶

Convert spherical polar coordinates to p-vector.

Parameters:	theta (float) – longitude angle in radians. phi (float) – latitude angle in radians. r (float) – radial distance.
Returns:	cartesian coordinates as a numpy.matrix of shape 1x3.

See also

SOFA manual.pdf page 212

pysofa.s2pv(theta, phi, r, td, pd, rd)¶

Convert position/velocity from spherical to cartesian coordinates.

Parameters:	theta (float) – longitude angle in radians. phi (float) – latitude angle in radians. r (float) – radial distance. td (float) – rate of change of theta. pd (float) – rate of change of phi. rd (float) – rate of change of r.
Returns:	pv-vector as a numpy.matrix of shape 2x3.

See also

SOFA manual.pdf page 213

pysofa.s2xpv(s1, s2, pv)¶

Multiply a pv-vector by two scalars.

Parameters:	s1 (float) – scalar to multiply position component by. s2 (float) – scalar to multiply velocity component by. pv (array-like of shape (2,3)) – pv-vector.
Returns:	a new pv-vector (with p scaled by s1 and v scaled by s2) as a numpy.matrix of shape 2x3.

See also

SOFA manual.pdf page 214

pysofa.sepp(a, b)¶

Angular separation between two p-vectors.

Parameters:	a (array-like of shape (1,3)) – first p-vector. b (array-like of shape (1,3)) – second p-vector.
Returns:	angular separation in radians, always positive (float).

See also

SOFA manual.pdf page 215

pysofa.seps(al, ap, bl, bp)¶

Angular separation between two sets of spherical coordinates.

Parameters:	al (float) – first longitude in radians. ap (float) – first latitude in radians. bl – second longitude in radians. bl (float) – second latitude in radians.
Returns:	angular separation in radians (float).

See also

SOFA manual.pdf page 216

pysofa.sxp(s, p)¶

Multiply a p-vector by a scalar.

Parameters:	s (float) – scalar. p (array-like of shape (1,3)) – p-vector
Returns:	s * p as a numpy.matrix of shape 1x3.

See also

SOFA manual.pdf page 222

pysofa.sxpv(s, pv)¶

Multiply a pv-vector by a scalar.

Parameters:	s (float) – scalar. pv (array-like of shape (2,3)) – pv-vector
Returns:	s * pv as a numpy.matrix of shape 2x3.

See also

SOFA manual.pdf page 223

pysofa.tf2a(s, ihour, imin, sec)¶

Convert hours, minutes, seconds to radians.

Parameters:	s – sign, ‘-‘ is negative, everything else positive. ihour (int) – hours. imin (int) – minutes. sec (float) – seconds.
Returns:	the converted value in radians (float).

See also

SOFA manual.pdf page 231

pysofa.tf2d(s, ihour, imin, sec)¶

Convert hours, minutes, seconds to days.

Parameters:	s – sign, ‘-‘ is negative, everything else positive. ihour (int) – hours. imin (int) – minutes. sec (float) – seconds.
Returns:	the converted value in days (float).

See also

SOFA manual.pdf page 232

pysofa.tr(r)¶

Transpose a rotation matrix.

Parameter:	r (array-like of shape (3,3)) – rotation matrix.
Returns:	transpose as a numpy.matrix of shape 3x3.

See also

SOFA manual.pdf page 233

pysofa.trxp(r, p)¶

Multiply a p-vector by the transpose of a rotation matrix.

Parameters:	r (array-like of shape (3,3)) – rotation matrix. p (array-like of shape (1,3)) – p-vector.
Returns:	numpy.matrix of shape 1x3.

See also

SOFA manual.pdf page 234

pysofa.trxpv(r, pv)¶

Multiply a pv-vector by the transpose of a rotation matrix.

Parameters:	r (array-like of shape (3,3)) – rotation matrix. pv (array-like of shape (2,3)) – pv-vector.
Returns:	numpy.matrix of shape 2x3.

See also

SOFA manual.pdf page 235

pysofa.zp(p)¶

Zero a p-vector.

Parameter:	p (array-like of shape (1,3)) – p-vector.
Returns:	a new p-vector filled with zeros. p isn’t modified.

See also

SOFA manual.pdf page 251

pysofa.zpv(pv)¶

Zero a pv-vector.

Parameter:	pv (array-like of shape (2,3)) – pv-vector.
Returns:	a new pv-vector filled with zeros. pv isn’t modified.

See also

SOFA manual.pdf page 252

pysofa.zr(r)¶

Initialize a rotation matrix to the null matrix.

Parameter:	r (array-like shape (3,3)) – rotation matrix.
Returns:	a new rotation matrix fileld with zeroes. r isn’t modified.

See also

SOFA manual.pdf page 253

Vector/Matrix/Angle functions¶

Previous topic

This Page

Navigation

Vector/Matrix/Angle functions¶

Previous topic

This Page

Quick search

Navigation