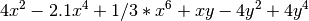Contents
1. wrapper_meigo module¶
Provide a Python interface to MEIGO (a R package).
>>> pymeigo import essR, rosen_for_r
>>> data = essR(f=rosen_for_r, x_L=[-1,-1], x_U=[2,2,])
The full documentation of the essR function comes from the R package itself.
In principle, you should not use this module directlty but the functions in the pymeigo.meigo module that provides the end-user tools and classes.
- essR(*args, **kargs)[source]¶
This is an automatic scan of the R manual. Layout may not be perfect...Please have a look at ssm_default() and set_problem_options().
Global optimization algorithm for MINLPs based on Scatter SearchKeyword : scatter search optimization
Description : essR attempts to solve problems of the form: min f(x,p_1,p_2,...,p_n) subject to: c_e=0 c_L le c(x) le c_U x_L le x le x_U % deqn{ min F(x) subject to: % x % ceq(x) = 0 (equality constraints)cr % c_L <= c(x) <= c_U (inequality constraints)cr % x_L <= x <= x_U (bounds on the decision variables)
Usage : essR(problem, opts = list(maxeval = NULL, maxtime = NULL), ...)
Parameters: - problem – List containing problem definition. opts List containing options (if set as opts <- numeric(0) default options will be loaded).
- ... – Additional variables passed to the objective function
Details : Problem definition: problem$f: Name of the file containing the objective function (String). problem$x_L: Lower bounds of decision variables (vector). problem$x_U: Upper bounds of decision variables (vector). problem$x_0: Initial point(s) (optional; vector or matrix). problem$f_0: Function values of initial point(s) (optional). These values MUST correspond to feasible points. NOTE: The dimension of f_0 and x_0 may be different. For example, if we want to introduce 5 initial points but we only know the values for 3 of them, x_0 would have 5 rows whereas f_0 would have only 3 elements. In this example, it is mandatory that the first 3 rows of x_0 correspond to the values of f_0. Fill the following fields if your problem has non-linear constraints: problem$neq: Number of equality constraints (Integer; do not define it if there are no equality constraints). problem$c_L: Lower bounds of nonlinear inequality constraints (vector). problem$c_U: Upper bounds of nonlinear inequality constraints (vector). problem$int_var: Number of integer variables (Integer). problem$bin_var: Number of binary variables (Integer). problem$vtr: Objective function value to be reached (optional). User options: opts$maxeval: Maximum number of function evaluations (Default 1000). opts$maxtime: Maximum CPU time in seconds (Default 60). opts$iterprint: Print each iteration on screen: 0-Deactivated; 1-Activated (Default 1). opts$plot: Plots convergence curves: 0-Deactivated; 1-Plot curves on line; 2-Plot final results (Default 0). opts$weight: Weight that multiplies the penalty term added to the objective function in constrained problems (Default 1e6). opts$log_var: Indexes of the variables which will be used to generate diverse solutions in different orders of magnitude (vector). opts$tolc: Maximum absolute violation of the constraints (Default 1e-5). opts$prob_bound: Probability (0-1) of biasing the search towards the bounds (Default 0.5). opts$inter_save: Saves results in a mat file in intermediate iterations. Useful for very long runs (Binary; Default = 0). Global options: opts$dim_refset: Number of elements in Refset (Integer; automatically calculated). opts$ndiverse: Number of solutions generated by the diversificator (Default 10*nvar). opts$combination: Type of combination of Refset elements (Default 1);1: hyper-rectangles; 2: linear combinations. Local options: opts$local_solver: Choose local solver 0: Local search deactivated (Default), “NM”, “BFGS”, “CG”, “LBFGSB”,”SA”,”SOLNP”. opts$local_tol: Level of tolerance in local search. opts$local_iterprint: Print each iteration of local solver on screen (Binary; default = 0). opts$local_n1: Number of iterations before applying local search for the 1st time (Default 1). opts$local_n2: Minimum number of iterations in the global phase between 2 local calls (Default 10). opts$local_balance: Balances between quality (=0) and diversity (=1) for choosing initial points for the local search (default 0.5). opts$local_finish: Applies local search to the best solution found once the optimization if finished (same values as opts.local.solver). opts$local_bestx: When activated (i.e. =1) only applies local search to the best solution found to date,ignoring filters (Default=0).
Value : fbest Best objective function value found after the optimization xbest Vector providing the best function value cpu_time Time in seconds consumed in the optimization f Vector containing the best objective function value after each iteration x Matrix containing the best vector after each iteration time Vector containing the cpu time consumed after each iteration neval Vector containing the number of function evaluations after each iteration numeval Number of function evaluations local_solutions Local solutions found by the local solver (in rows) local_solutions_values Function values of the local solutions end_crit Criterion to finish the optimization: ll 1 Maximal number of function evaluations achieved 2 Maximum allowed CPU Time achieved 3 Value to reach achieved
Note : R code of the eSS optimization code from: Process Engineering Group IIM-CSIC. Constraint functions, if applicable, must be declared in the same script as the objective function as a second output argument, e.g.: myfunction <- function(x){ calculate fx - scalar containing the objective function value calculate gx - vector (or empty) containing the constraints values return(list(fx,gx)) }
Author : Jose Egea
References : If you use essR and publish the results, please cite the following papers: Egea, J.A., Maria, R., Banga, J.R. (2010) An evolutionary method for complex-process optimization. Computers & Operations Research 37(2): 315-324. Egea, J.A., Balsa-Canto, E., Garcia, M.S.G., Banga, J.R. (2009) Dynamic optimization of nonlinear processes with an enhanced scatter search method. Industrial & Engineering Chemistry Research 49(9): 4388-4401.
Example:
#1 Unconstrained problem ex1 <- function(x){ y<-4*x[1]*x[1]-2.1*x[1]^4+1/3*x[1]^6+x[1]*x[2]-4*x[2]*x[2]+4*x[2]^4; return(y) } #global optimum #x*=[0.0898, -0.7127]; # or #x*=[-0.0898, 0.7127]; # #f(x*)= -1.03163; #========================= PROBLEM SPECIFICATIONS =========================== problem<-list(f="ex1",x_L=rep(-1,2),x_U=rep(1,2)) opts<-list(maxeval=500, ndiverse=10, dim_refset=4, local_solver="solnp", local_n2=1) #========================= END OF PROBLEM SPECIFICATIONS ===================== Results<-essR(problem,opts); #2 Constrained problem ex2<-function(x){ F=-x[1]-x[2]; g<-rep(0,2); g[1]<-x[2]-2*x[1]^4+8*x[1]^3-8*x[1]^2; g[2]<-x[2]-4*x[1]^4+32*x[1]^3-88*x[1]^2+96*x[1]; return(list(F=F,g=g)) } # global optimum #x*=[2.32952, 3.17849]; #f(x*)=-5.50801 #========================= PROBLEM SPECIFICATIONS =========================== problem<-list(f="ex2",x_L=rep(0,2),x_U=c(3,4), c_L=rep(-Inf,2), c_U=c(2,36)) opts<-list(maxeval=750, local_solver="solnp", local_n2=1) #========================= END OF PROBLEM SPECIFICATIONS ===================== Results<-essR(problem,opts); #3 Constrained problem with equality constraints ex3<-function(x,k1,k2,k3,k4){ f=-x[4]; #Equality constraints g<-rep(0,5); g[1]=x[4]-x[3]+x[2]-x[1]+k4*x[4]*x[6]; g[2]=x[1]-1+k1*x[1]*x[5]; g[3]=x[2]-x[1]+k2*x[2]*x[6]; g[4]=x[3]+x[1]-1+k3*x[3]*x[5]; #Inequality constraint g[5]=x[5]^0.5+x[6]^0.5; return(list(f=f,g=g)); } #global optimum #x*=[0.77152 # 0.516994 # 0.204189 # 0.388811 # 3.0355 # 5.0973]; # #f(x*)= -0.388811; #========================= PROBLEM SPECIFICATIONS =========================== problem<-list(f="ex3",x_L=rep(0,6),x_U=c(rep(1,4),16,16), neq=4, c_L=-Inf, c_U=4) opts<-list(maxtime=7, local_solver="solnp", local_n2=10) #========================= END OF PROBLEM SPECIFICATIONS ===================== k1=0.09755988; k3=0.0391908; k2=0.99*k1; k4=0.9*k3; Results<-essR(problem,opts,k1,k2,k3,k4); #4 Mixed integer problem ex4<-function(x){ F = x[2]^2 + x[3]^2 + 2.0*x[1]^2 + x[4]^2 - 5.0*x[2] - 5.0*x[3] - 21.0*x[1] + 7.0*x[4]; g<-rep(0,3); g[1] = x[2]^2 + x[3]^2 + x[1]^2 + x[4]^2 + x[2] - x[3] + x[1] - x[4]; g[2] = x[2]^2 + 2.0*x[3]^2 + x[1]^2 + 2.0*x[4]^2 - x[2] - x[4]; g[3] = 2.0*x[2]^2 + x[3]^2 + x[1]^2 + 2.0*x[2] - x[3] - x[4]; return(list(F=F, g=g)); } # global optimum #x*=[2.23607, 0, 1, 0]; #f(x*)=-40.9575; #========================= PROBLEM SPECIFICATIONS =========================== problem<-list(f="ex4", x_L=rep(0,4), x_U=rep(10,4), x_0=c(3,4,5,1),int_var=3, c_L=rep(-Inf,3), c_U=c(8,10,5)) opts<-list(maxtime=2) #========================= END OF PROBLEM SPECIFICATIONS ===================== Results<-essR(problem,opts);
- vns_default()[source]¶
VNS default parameters
Assigns default values for all the options
Parameters: - maxeval (int) – Maximum number of function evaluations (1000)
- maxtime (int) – Maximum CPU time (default is 60 seconds)
- maxdist (float) – Percentage of the problem dimension which will be perturbed in the furthest neighborhood (vary between 0-1) (default is 0.5)
- use_local (int) – Uses local search (1) or not (0)
The following options only apply if use_local is active
Parameters: - aggr (int) – Aggressive search. The local search is only applied when the best solution has been improved (1=aggressive search , 0=non-aggressive search).
- local_search_type (int) – Applies a first (=1) or a best (=2) improvement scheme for the local search.
- decomp (int) – Decompose the local search (=1) using only the variables perturbed in the global phase.
- ssm_default()[source]¶
Return the default parameters required by the SSM algorithm.
List containing options (if set as opts <- numeric(0) default options will be loaded). See the script of default options to know their values
User options: - inter_save = Saves results of intermediate iterations in eSSR_report.RData Useful for very long runs. (Binary; Default = 0)
- iterprint = Print each iteration on screen: 0-Deactivated 1-Activated (Default 1)
- log_var = Indexes of the variables which will be used to generate diverse solutions in different orders of magnitude (vector)
- maxeval = Maximum number of function evaluations (Default 1000)
- maxtime = Maximum CPU time in seconds (Default 60)
- prob_bound = Probability (0-1) of biasing the search towards the bounds (Default 0.5)
- tolc = Maximum absolute violation of theconstraints (Default 1e-5)
- weight = Weight that multiplies the penalty term added to the objective function in constrained problems (Default 1e6)
Global options: - combination: Type of combination of Refset elements (Default 1)
- hyper-rectangles
- linear combinations
dim_refset: Number of elements in Refset (Integer; automatically calculated)
ndiverse: Number of solutions generated by the diversificator (Default 10*nvar)
Local options: - local_solver: Choose local solver 0: Local search deactivated (Default), “NM”, “BFGS”, “CG”, “LBFGSB”, “SA”,”SOLNP”, “DHC”, “NLS2SOL”
- local_tol: Level of tolerance in local search
- local_iterprint: print each iteration of local solver on screen (Binary; default = 0)
- local_n1: Number of iterations before applying local search for the 1st time (Default 1)
- local_n2: Minimum number of iterations in the global phase between 2 local calls (Default 10)
- local_balance: Balances between quality (=0) and diversity (=1) for choosing initial points for the local search (default 0.5)
- local_finish: Applies local search to the best solution found once the optimization if finished (same values as opts.local.solver)
- local_bestx: When activated (i.e. =1) only applies local search to the best solution found to date,ignoring filters (Default=0)
- set_problem_options(f=None, x_L=[], x_U=[], x_0=None, f_0=None, neq=None, c_L=None, c_U=None, int_var=None, bin_var=None, vtr=None, **kargs)[source]¶
INPUT PARAMETERS:
Parameters: - f – Name of the file containing the objective function (String)
- x_L – Lower bounds of decision variables (vector)
- x_U – Upper bounds of decision variables (vector)
- x_0 – Initial point(s) (optional; vector or matrix)
- f_0 – Function values of initial point(s) (optional)
Note
The dimension of f_0 and x_0 may be different. For example, if we want to introduce 5 initial points but we only know the values for 3 of them, x_0 would have 5 rows whereas f_0 would have only 3 elements. In this example, it is mandatory that the first 3 rows of x_0 correspond to the values of f_0
Additionally, fill the following fields if your problem has non-linear constraints
Parameters: - neq – Number of equality constraints (Integer; do not define it if there are no equality constraints)
- c_L – Lower bounds of nonlinear inequality constraints (vector)
- c_U – Upper bounds of nonlinear inequality constraints (vector)
- int_var – Number of integer variables (Integer)
- bin_var – Number of binary variables (Integer)
- vtr – Objective function value to be reached opional)
- rvnds_hamming(*args, **kargs)[source]¶
This is an automatic scan of the R manual. Layout may not be perfect...Please have a look at ssm_default() and set_problem_options().
Main VNS functionDescription : VNS Kernel function
Usage : rvnds_hamming(problem, opts, ...)
Parameters: - problem – List containing problem settings definition.
- opts – List containing options (if set as opts <- numeric(0) default options will be loaded). Additional variables passed to the objective function
Details : problem$f: Name of the file containing the objective function (String). problem$x_L: Lower bounds of decision variables (vector). problem$x_U: Upper bounds of decision variables (vector). problem$x_0: Initial point(s) (optional; vector or matrix). problem$f_0: Function values of initial point(s) (optional). These values MUST correspond to feasible points. User options: opts$maxeval: Maximum number of function evaluations (Default 1000). opts$maxtime: Maximum CPU time in seconds (Default 60). opts$maxdist: Percentage of the problem dimension which will be perturbed in the furthest neighborhood (varies between 0 and1, default is 0.5). opts$use_local: Uses local search (1) or not (0). The default is 1. The following options only apply when the local search is activated: opts$use_aggr: Aggressive search. The local search is only applied when the best solution has been improved (1=aggressive search, 0=non-aggressive search, default:0). opts$local search type: Applies a first (=1) or a best (=2) improvement scheme for the local search (Default: 1). opts$decomp: Decompose the local search (=1) using only the variables perturbed in the global phase. Default: 1.
Value : fbest Best objective function value found after the optimization xbest Vector providing the best function value cpu_time Time in seconds consumed in the optimization func Vector containing the best objective function value after each iteration x Matrix containing the best vector after each iteration time Vector containing the cpu time consumed after each iteration neval Vector containing the number of function evaluations after each iteration numeval Number of function evaluations
Example:
library(MEIGOR) source(system.file("/benchmarks/rosen10.R",package="MEIGOR")); nvar<-10; problem<-list(f="rosen10", x_L=rep(-5,nvar), x_U=rep(1,nvar)) opts<-list(maxeval=2000, maxtime=3600*69, use_local=1, aggr=0, local_search_type=1, decomp=1, maxdist=0.5) algorithm<-"VNS"; Results<-MEIGO(problem,opts,algorithm);
- MEIGO(*args, **kargs)[source]¶
MEIGO main function
Description : Wrapper around the different optimisation methods
Usage : MEIGO(problem, opts, algorithm, ...)
Parameters: - problem – List containing problem settings.
- opts – A list of n_threads lists containing options for each cooperative instance of essR.
- algorithm – One of VNS, ESS, MULTISTART, CESSR, CEVNSR. Check the documentation of each algorithm for more information.
- ... – Additional input arguments.
See also
:func:` , :func:`essR, :func:` , :func:`rvnds_hamming, :func:` , :func:`CeVNSR, :func:` , :func:`CeSSR
Example:
#global optimum #x*=[0.0898, -0.7127]; # or #x*=[-0.0898, 0.7127]; # #f(x*)= -1.03163; library(MEIGOR) source(system.file("/benchmarks/ex1.R",package="MEIGOR")); #========================= PROBLEM SPECIFICATIONS =========================== problem<-list(f=ex1,x_L=rep(-1,2),x_U=rep(1,2)) opts<-list(maxeval=500, ndiverse=40, local_solver='DHC', local_finish='LBFGSB', local_iterprint=1) #========================= END OF PROBLEM SPECIFICATIONS ===================== Results<-MEIGO(problem,opts,algorithm="ESS");
2. funcs module¶
This module provides some function to play with
- pyfunc2R(f)[source]¶
Converts a python function into a R object
def f(x,y): return x+y f4r = pyfunc2R(f)
- rosen_for_r = <rpy2.rinterface.SexpClosure - Python:0x3254948 / R:0x1415fe30>¶
wrap the function rosen so it can be exposed to R
- example_unconstrained_for_r = <rpy2.rinterface.SexpClosure - Python:0x32549d8 / R:0x1415ea50>¶
wrap the function test1 so it can be exposed to R
3. meigo module¶
Provide a class to run MEIGO optimisation (ESS and VNS algorithms)
- class ESS(f)[source]¶
Interface to the ESS algorithm
from pymeigo import ESS, rosen_for_r m = ESS(f=rosen_for_r) m.run(x_U=[2,2], x_L=[-1,-1]) m.plot()
See also
Constructor
Parameters: f (str) – the objective function - algorithm¶
Returns optimisation algorithm
- plot()¶
plotting the evolution of the cost function
- run(x_U=[2, 2], x_L=[-1, -1], **kargs)[source]¶
Runs the optimisation
Parameters: - x_U – upper limit of the parameter
- x_U – lower limit of the parameter
- bin_var – number of variables of binary type
Returns: an object containing the results of the optimisation. See MEIGO for details.
See also
set_problem_options() for arguments related to the objective function.
See also
ssm_default() for arguments related to SSM algorithm.
- class VNS(f)[source]¶
Interface to the VNS algorithm
from pymeigo import ESS, rosen_for_r m = ESS(f=rosen_for_r) m.run(x_U=[2,2], x_L=[-1,-1]) m.plot()
See also
Constructor
Parameters: f (str) – the objective function - algorithm¶
Returns optimisation algorithm
- plot()¶
plotting the evolution of the cost function
- run(x_U, x_L, **kargs)[source]¶
Runs the optimisation
Parameters: - x_U – upper limit of the parameter
- x_U – lower limit of the parameter
- bin_var – number of variables of binary type
Returns: an object containing the results of the optimisation. See MEIGO for details.
See also
set_problem_options() for arguments related to the objective function.
See also
ssm_default() for arguments related to SSM algorithm.
- class MEIGO(algorithm, f)[source]¶
Interface to several optimisation algorithm
from pymeigo import MEIGO, rosen_for_r m = MEIGO("ESS", f=rosen_for_r) m.run(x_U=[2,2], x_L=[-1,-1]) m.plot()
Constructor
Parameters: - algorithm (str) – the algorithm in [“ESS”, “VNS”]
- f (str) – the objective function
- algorithm¶
Returns optimisation algorithm
- plot()¶
plotting the evolution of the cost function
- run(x_U, x_L, **kargs)[source]¶
Runs the optimisation
Parameters: - x_U – upper limit of the parameter
- x_U – lower limit of the parameter
- bin_var – number of variables of binary type
Returns: an object containing the results of the optimisation. See MEIGO for details.
See also
set_problem_options() for arguments related to the objective function.
See also
vns_default() for arguments related to VNS algorithm.
See also
ssm_default() for arguments related to SSM algorithm.