PyChemia CookBook¶
This is a set of small recipes for getting the ‘job done’ quickly using the methods and classes implemented on PyChemia
Reading a formula and extracting the composition¶
Consider that you have a formula such as ‘YBa2Cu3O7’ and you would like to get the composition and the number of atoms of each species. The recipe is very simple:
>>> import pychemia
>>> formula = 'YBa2Cu3O7'
>>> comp = pychemia.Composition(formula)
>>> comp['Ba']
2
The Composition object acts like a python dictionary, with the particularity of returning 0 when we ask for species non present on a given composition:
>>> comp['Au']
0
Converting an ascii file into a POSCAR¶
Consider the following ascii file stored on test.ascii:
None
11.47012476778924 0.79937702290141 9.51246277071292
-2.99939838492446 -0.12947182393907 7.79142604544631
0.6793241103939325 -0.0865078526005124 5.2059167421975845 Mg
7.2961243488047218 7.8694796435395364 5.3644840894866279 Mg
2.9186811537636199 0.3979635592494910 1.4510323645408516 Ca
-0.9269026176064651 2.5195450955593404 2.9685499969876323 Ca
-0.8684364924472798 6.8223765997007311 5.7332541305138323 Ca
7.7311137749974712 6.1831255116012693 0.0000000000000000 Ca
This is how pychemia can convert it into a POSCAR file:
>>> import pychemia
>>> st = pychemia.io.ascii.load('test.ascii')
>>> pychemia.code.vasp.write_poscar(st, 'POSCAR.test')
The final archive called POSCAR.test will looks like this:
Mg Ca
1.0
11.4701247677892404 0.0000000000000000 0.0000000000000000
0.7993770229014100 9.5124627707129203 0.0000000000000000
-2.9993983849244601 -0.1294718239390700 7.7914260454463102
Mg Ca
2 4
Direct
0.2339469912681612 1.0000000000000000 0.6681596811459407
0.7578333625215485 0.8366521516169854 0.6885111991304717
0.3000667985403045 0.0443708102021889 0.1862345039376849
0.0000000000000000 0.2700535286675975 0.3810021400026761
0.0660256684506364 0.7272193856947440 0.7358414360955946
0.6287217253130448 0.6500025977119140 0.0000000000000000
Compute the hardness of a given structure¶
Compute the ideal strength¶
Read and Write structures between several atomistic codes¶
Search for structures from the PyChemia database¶
Generate and manipulate VASP input files¶
Convergence studies for VASP¶
Read and write the input from an atomistic code¶
Read the output from an atomistic code¶
Build an manipulate the lattice¶
Rotate the cell along a Miller index¶
Very often for creating surfaces we need to rotate the structure along specific Miller indices. We can achieve this with a routine for that, see this example:
import pychemia
pychemia_path = pychemia.__path__[0]
st=pychemia.code.vasp.read_poscar(pychemia_path + '/test/data/vasp_06/POSCAR')
st2=pychemia.analysis.surface.rotate_along_indices(st, 1,1,1, 2)
Both structures represent the same crystal, the second structure has the ‘c’ axis parallel to the 111 Miller direction. Additionally we ask for having 2 layers of the cristal along the ‘c’ axis. We can check that the symmetry of the crystal remains the same:
sym=pychemia.crystal.CrystalSymmetry(st)
sym.number()
139
sym=pychemia.crystal.CrystalSymmetry(st2)
sym.number()
139
Here you see the result of the two structures, the original and the rotated along the 111 axis.
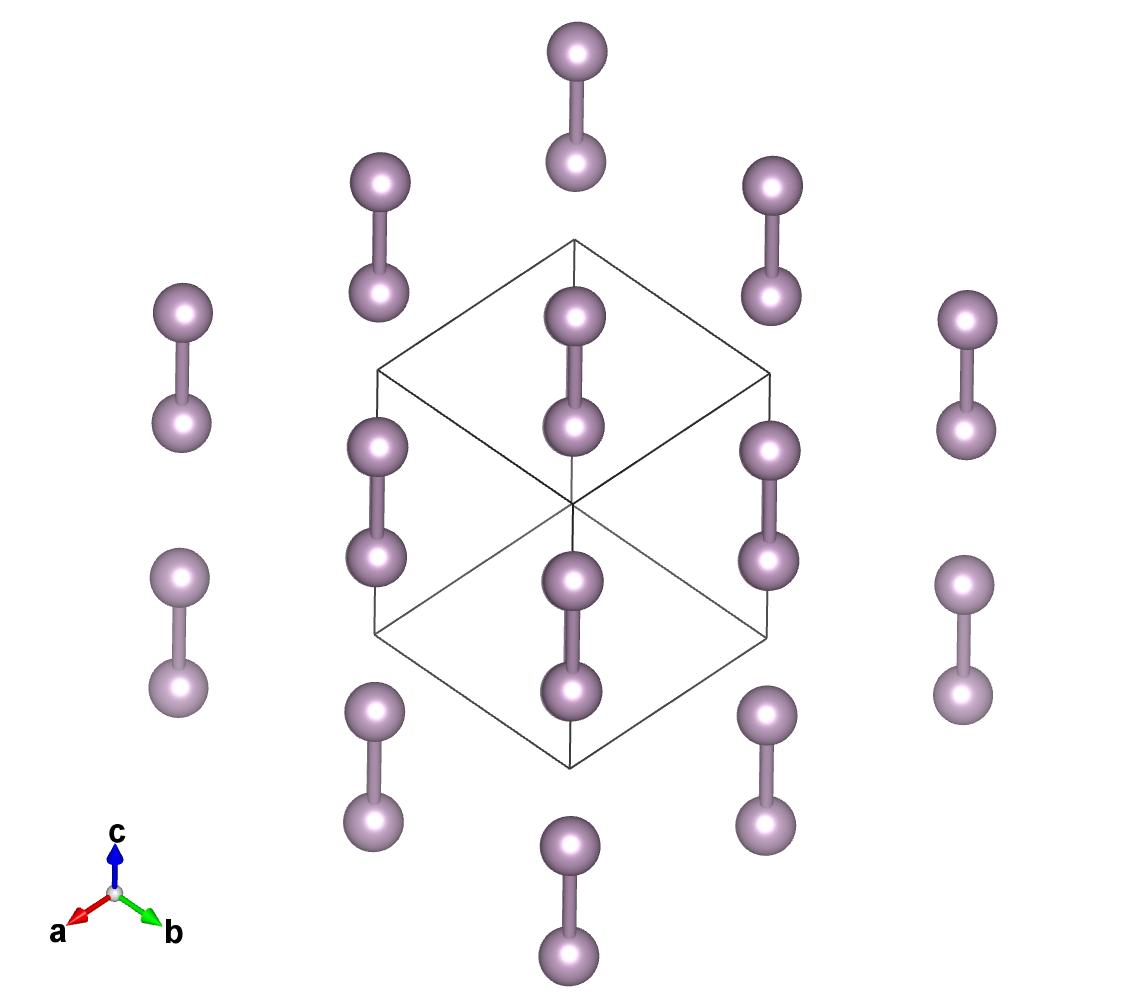
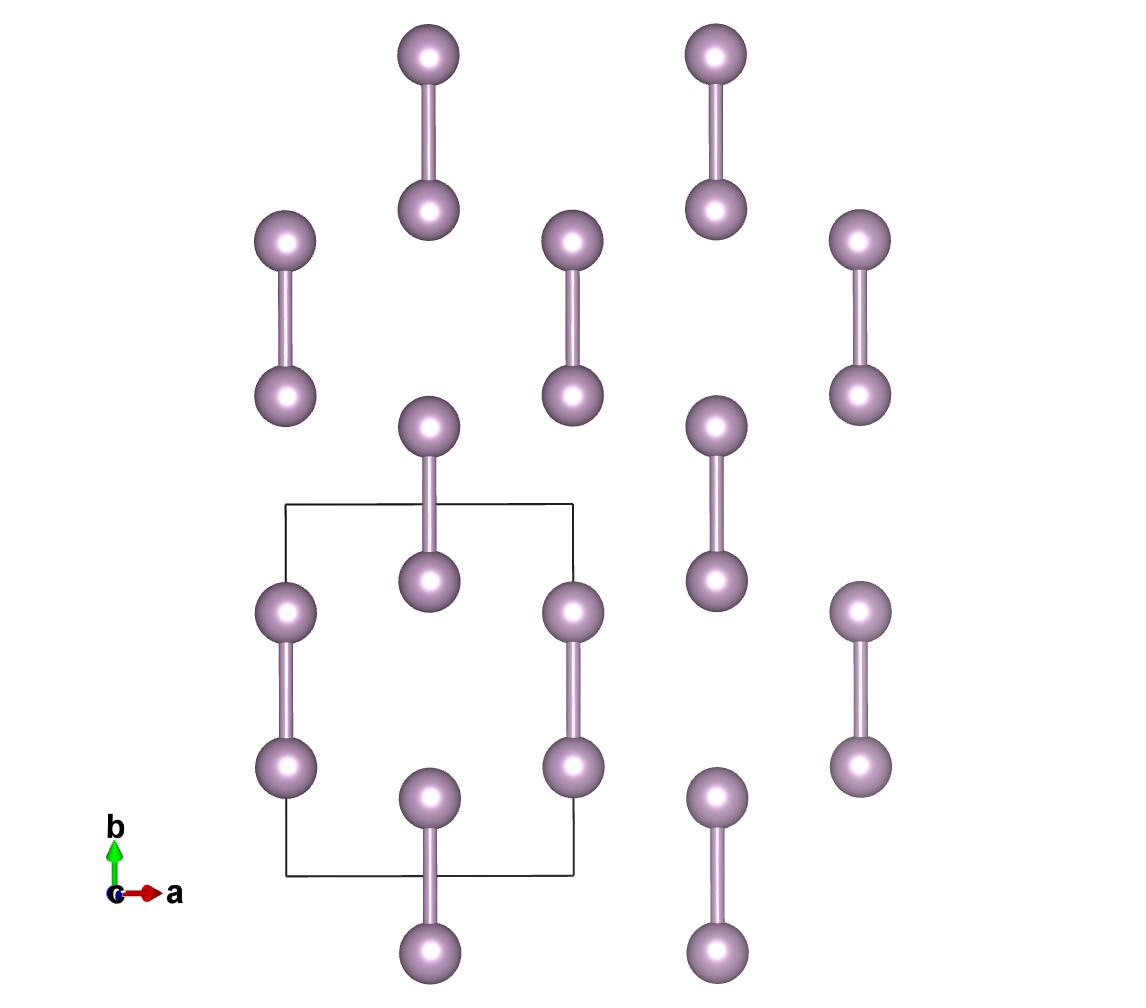
Get the spatial group¶
Lets start reading a POSCAR for a Carbon diamond structure:
import pychemia
pychemia_path = pychemia.__path__[0]
st=pychemia.code.vasp.read_poscar(pychemia_path + '/test/data/vasp_08/POSCAR_old')
print(st)
You should get:
2
Symb ( Positions ) [ Cell-reduced coordinates ]
C ( 0.0000 0.0000 0.0000 ) [ 0.0000 0.0000 0.0000 ]
C ( 0.9250 0.9250 0.9250 ) [ 0.2500 0.2500 0.2500 ]
Periodicity: X Y Z
Lattice vectors:
1.8500 1.8500 0.0000
0.0000 1.8500 1.8500
1.8500 0.0000 1.8500
PyChemia uses spglib to get the space-group and use some other routines to get the primitive and convectional cells and
to reposition the atoms to precise positions for a given symmetry. All this functionality is provided by creating
CrystalSymmetry object:
sym=pychemia.crystal.CrystalSymmetry(st)
We can get space groups using the number:
sym.number()
227
Or as internation symbol:
sym.symbol()
'Fd-3m'
In both cases, there is a tolerance that can be adjusted, the default value is 1e-5 that could be too strong for structures produced by DFT calculations with crude relaxations.
To exemplify this situation consider this structure (Zn2V2O7) whit positions truncated to 4 decimals:
st = pychemia.code.vasp.read_poscar(pychemia_path + '/test/data/vasp_07/POSCAR_trunc')
sym = pychemia.crystal.CrystalSymmetry(st)
sym.number()
You will get space group equal to 9, however adjusting the tolerance you will get the value from the precise structure:
sym.number(1E-2)
15
And the same works for the symbol:
sym.symbol(1E-2)
'C2/c'
Get the primitive cell¶
The primitive cell is obtained from the CrystalSymmetry object again using the functionality of the spglib
library:
import pychemia
pychemia_path = pychemia.__path__[0]
st = pychemia.code.vasp.read_poscar(pychemia_path + '/test/data/vasp_06/POSCAR')
sym = pychemia.crystal.CrystalSymmetry(st)
print(st)
The structure looks like this:
4
Symb ( Positions ) [ Cell-reduced coordinates ]
P ( 0.0000 0.0000 3.7190 ) [ 0.0000 0.0000 0.7078 ]
P ( 0.0000 0.0000 1.5350 ) [ 0.0000 0.0000 0.2922 ]
P ( 2.0308 2.0308 1.0920 ) [ 0.5000 0.5000 0.2078 ]
P ( 2.0308 2.0308 4.1620 ) [ 0.5000 0.5000 0.7922 ]
Periodicity: X Y Z
Lattice vectors:
4.0616 0.0000 0.0000
0.0000 4.0616 0.0000
0.0000 0.0000 5.2540
We can get the primitive like this (eventually using a tolerance as an argument):
stp = sym.find_primitive()
print(stp)
And the structure is reduced to a cell with just 2 atoms:
2
Symb ( Positions ) [ Cell-reduced coordinates ]
P ( 0.0000 0.0000 1.5350 ) [ 0.2922 0.2922 0.0000 ]
P ( 0.0000 0.0000 3.7190 ) [ 0.7078 0.7078 0.0000 ]
Periodicity: X Y Z
Lattice vectors:
-2.0308 2.0308 2.6270
2.0308 -2.0308 2.6270
2.0308 2.0308 -2.6270
Get the conventional cell¶
The conventional cell is obtained as a result of the refinement of the cell, ie adjusting the positions precisely to satisfy a given tolerance. From the previous section, lets reconstruct a convectional cell from the primitive:
sym = pychemia.crystal.CrystalSymmetry(stp)
stc = sym.refine_cell()
print(stc)
You should get:
4
Symb ( Positions ) [ Cell-reduced coordinates ]
P ( 0.0000 0.0000 1.5350 ) [ 0.0000 0.0000 0.2922 ]
P ( 0.0000 0.0000 3.7190 ) [ 0.0000 0.0000 0.7078 ]
P ( 2.0308 2.0308 4.1620 ) [ 0.5000 0.5000 0.7922 ]
P ( 2.0308 2.0308 1.0920 ) [ 0.5000 0.5000 0.2078 ]
Periodicity: X Y Z
Lattice vectors:
4.0616 0.0000 0.0000
0.0000 4.0616 0.0000
0.0000 0.0000 5.2540
Now lets refine the structure with positions truncated and reconstruct a cell with positions precisely in place to the symmetry found:
st = pychemia.code.vasp.read_poscar(pychemia_path + '/test/data/vasp_07/POSCAR_trunc')
sym = pychemia.crystal.CrystalSymmetry(st)
st2 = sym.refine_cell(1E-2)
sym = pychemia.crystal.CrystalSymmetry(st2)
Here we took the structure with positions truncated, and refined the cell using a tolerance that return the an space
group 15, after that we create a new CrystalSymmetry object from the new structure and we can verify that the space
group is preserved up to very strict tolerances:
sym.number()
15
sym.number(1E-14)
15