Response Surface Designs

In this section, the following kinds of response surface designs will be described:

• Box-Behnken
• Central Composite

Hint

All available designs can be accessed after a simple import statement:

>>> from pyDOE import *

Box-Behnken (bbdesign)

Box-Behnken designs can be created using the following simple syntax:

>>> bbdesign(n, center)

where n is the number of factors (at least 3 required) and center is the number of center points to include. If no inputs given to center, then a pre-determined number of points are automatically included.

Examples

The default 3-factor Box-Behnken design:

>>> bbdesign(3)
array([[-1., -1.,  0.],
       [ 1., -1.,  0.],
       [-1.,  1.,  0.],
       [ 1.,  1.,  0.],
       [-1.,  0., -1.],
       [ 1.,  0., -1.],
       [-1.,  0.,  1.],
       [ 1.,  0.,  1.],
       [ 0., -1., -1.],
       [ 0.,  1., -1.],
       [ 0., -1.,  1.],
       [ 0.,  1.,  1.],
       [ 0.,  0.,  0.],
       [ 0.,  0.,  0.],
       [ 0.,  0.,  0.]])

A customized design with four factors, but only a single center point:

>>> bbdesign(4, center=1)
array([[-1., -1.,  0.,  0.],
       [ 1., -1.,  0.,  0.],
       [-1.,  1.,  0.,  0.],
       [ 1.,  1.,  0.,  0.],
       [-1.,  0., -1.,  0.],
       [ 1.,  0., -1.,  0.],
       [-1.,  0.,  1.,  0.],
       [ 1.,  0.,  1.,  0.],
       [-1.,  0.,  0., -1.],
       [ 1.,  0.,  0., -1.],
       [-1.,  0.,  0.,  1.],
       [ 1.,  0.,  0.,  1.],
       [ 0., -1., -1.,  0.],
       [ 0.,  1., -1.,  0.],
       [ 0., -1.,  1.,  0.],
       [ 0.,  1.,  1.,  0.],
       [ 0., -1.,  0., -1.],
       [ 0.,  1.,  0., -1.],
       [ 0., -1.,  0.,  1.],
       [ 0.,  1.,  0.,  1.],
       [ 0.,  0., -1., -1.],
       [ 0.,  0.,  1., -1.],
       [ 0.,  0., -1.,  1.],
       [ 0.,  0.,  1.,  1.],
       [ 0.,  0.,  0.,  0.]])

Central Composite (ccdesign)

Central composite designs can be created and customized using the syntax:

>>> ccdesign(n, center, alpha, face)

where

• n is the number of factors,
• center is a 2-tuple of center points (one for the factorial block, one for the star block, default (4, 4)),
• alpha is either “orthogonal” (or “o”, default) or “rotatable” (or “r”)
• face is either “circumscribed” (or “ccc”, default), “inscribed” (or “cci”), or “faced” (or “ccf”).

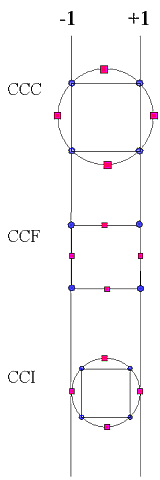
The two optional keyword arguments alpha and face help describe how the variance in the quadratic approximation is distributed. Please see the NIST web pages if you are uncertain which options are suitable for your situation.

Note

• ‘ccc’ and ‘cci’ can be rotatable designs, but ‘ccf’ cannot.
• If face is specified, while alpha is not, then the default value of alpha is ‘orthogonal’.

Examples

Simplest input, assuming default kwargs:

>>> ccdesign(2)
array([[-1.        , -1.        ],
       [ 1.        , -1.        ],
       [-1.        ,  1.        ],
       [ 1.        ,  1.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [-1.41421356,  0.        ],
       [ 1.41421356,  0.        ],
       [ 0.        , -1.41421356],
       [ 0.        ,  1.41421356],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ],
       [ 0.        ,  0.        ]])

More customized input, say, for a set of computer experiments where there isn’t variability so we only need a single center point:

>>> ccdesign(3, center=(0, 1), alpha='r', face='cci')
array([[-0.59460356, -0.59460356, -0.59460356],
       [ 0.59460356, -0.59460356, -0.59460356],
       [-0.59460356,  0.59460356, -0.59460356],
       [ 0.59460356,  0.59460356, -0.59460356],
       [-0.59460356, -0.59460356,  0.59460356],
       [ 0.59460356, -0.59460356,  0.59460356],
       [-0.59460356,  0.59460356,  0.59460356],
       [ 0.59460356,  0.59460356,  0.59460356],
       [-1.        ,  0.        ,  0.        ],
       [ 1.        ,  0.        ,  0.        ],
       [ 0.        , -1.        ,  0.        ],
       [ 0.        ,  1.        ,  0.        ],
       [ 0.        ,  0.        , -1.        ],
       [ 0.        ,  0.        ,  1.        ],
       [ 0.        ,  0.        ,  0.        ]])

More Information

If the user needs more information about appropriate designs, please consult the following articles on Wikipedia:

• Box-Behnken designs
• Central composite designs

There is also a wealth of information on the NIST website about the various design matrices that can be created as well as detailed information about designing/setting-up/running experiments in general.

Any questions, comments, bug-fixes, etc. can be forwarded to the author.