optimize Package¶
optimize Package¶
optimize¶
This package deals with the optimization of generalized integrate and fire neurons (gLIF).
fit_gLIF Module¶
fit_gLIF¶
Fits subthreshold and threshold parameters of a gLIF model from voltage patch clamp data. A neuron object is returned to the client that can easily be simulated using standard methods listed in the documentation.
- fit_neuron.optimize.fit_gLIF.fit_neuron(input_current_list=None, membrane_voltage_list=None, dt=None, volt_nonlin_fcn=None, sic_list=None, t_thresh_bins=[], volt_adapt_time_const=[], thresh_param_init=None, max_lik_iter_max=20, process_ct=None, stopping_criteria=0.01, look_behind=0.002)[source]¶
Fits an actionable neuron to the data provided.
Parameters: - input_current_list – list of arrays of recorded current injections.
- membrane_voltage_list – list of arrays of recorded membrane voltages corresponding to input_current_list input.
- dt – time step.
- volt_nonlin_fcn – voltage nonlinearity function (see fit_neuron.optimize.subthreshold.Voltage).
- sic_list – list of spike induced current objects (see fit_neuron.optimize.sic_lib).
- t_thresh_bins – list of endpoints of time intervals used to compute step-like threshold (see fit_neuron.optimize.threshold.StochasticThresh).
- volt_adapt_time_const – list of time constancs
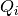 for voltage chasing currents. (see fit_neuron.optimize.threshold.StochasticThresh).
for voltage chasing currents. (see fit_neuron.optimize.threshold.StochasticThresh). - thresh_param_init – initial value of threshold parameters for max likelihood threshold optimization (see fit_neuron.optimize.threshold.max_likelihood()).
- make_lik_iter_max – maximum number of max likelihood iterations (see fit_neuron.optimize.threshold.max_likelihood()).
- process_ct – number of processors we want to use to distribute max likelihood; if None then use max CPU count (see fit_neuron.optimize.threshold.max_likelihood()).
- stopping_criteria – minimum
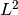 norm of log likelihood gradient below which we stop optimization (see fit_neuron.optimize.threshold.max_likelihood()).
norm of log likelihood gradient below which we stop optimization (see fit_neuron.optimize.threshold.max_likelihood()). - look_behind – parameter that controls how the length of the refractory period is computed (see fit_neuron.data.my_data.raw_2_processed()).
Returns:
neuron_base_obj Module¶
- class fit_neuron.optimize.neuron_base_obj.Neuron(subthresh_obj=None, thresh_obj=None, V_init=None)[source]¶
Return type of optimization procedure.
- get_param_dict()[source]¶
Extracts and returns parameter dictionaries from the subthreshold and threshold parts of the neuron.
sic_lib Module¶
This file will contain a library of spike induced current (sic) objects. A user may provide any list of spike induced current objects to the optimization functions as long as all of these objects are derived from the SicBase abstract class or implement methods with the same names and input arguments.
- class fit_neuron.optimize.sic_lib.ExpDecay_sic(k=None, dt=0.0001)[source]¶
Bases: fit_neuron.optimize.sic_lib.SicBase
Exponentially decaying spike induced current. The class models the following differential equation:
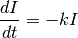
When the neuron spikes, the current
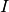 is incremented as follows:
is incremented as follows: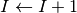
- dt = None¶
time step
- k = None¶
decay rate
- sic_val = None¶
value of the spike induced current
- class fit_neuron.optimize.sic_lib.StepSic(t_max, dt=0.0001)[source]¶
Bases: fit_neuron.optimize.sic_lib.SicBase
Step wise spike induced current that is the sum of indicator variables for the spiking history of the time since the last spike being between zero and some t_max.
- dt = None¶
time increments
- sic_val = None¶
actual value of the spike induced current
- t_hist = None¶
list of time elapsed since last spikes
- t_max = None¶
time defining indicator functions
subthreshold Module¶
subthreshold¶
Parameter extraction of subthreshold parameters from voltage clamp data. This module defines a subthreshold model (Voltage) and defines an optimization function (estimate_volt_parameters()).
- class fit_neuron.optimize.subthreshold.Voltage(param_dict={}, param_arr=[], sic_list=[], volt_nonlin_fcn=None, dt=0.0001, Vr=-70.0, V_rest=-75.0, t_ref=0.004)[source]¶
This class defines the voltage predictions of the gLIF models.
Parameters: - param_dict – dictionary of parameter values.
- param_arr – array of parameter values.
- sic_list – list of fit_neuron.optimize.sic_lib.SicBase instances.
- volt_nonlin_fcn – voltage nonlinearity function.
- Vr – reset value of the voltage following a spike and a refractory period.
- V_rest – voltage resting value
- t_ref – length of refractory period in seconds.
- dt – time increment.
The difference equation describing the evolution of the membrane potential is the following:
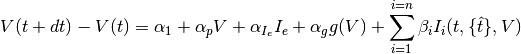
where
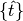 are the previous spike times relative to the current time
are the previous spike times relative to the current time 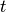 ,
the
,
the 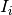 are the spike induced currents, which may or may not depend explicitly on
are the spike induced currents, which may or may not depend explicitly on 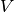 ,
and
,
and 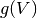 is an optional voltage nonlinearity function.
is an optional voltage nonlinearity function.The updates are implemented as follows:
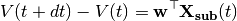
where
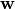 is the parameter vector, and
is the parameter vector, and![{\bf X_{sub}} = [V,1,I_e,g(V),{\bf I}(t)^{\top}]^{\top}](_images/math/609afa9a329782f0f53eaed6dbeaae3c944f8dbc.png)
The vector
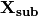 is computed at each time step by
compute_X_subthresh() and the inner product is taken
by update().
is computed at each time step by
compute_X_subthresh() and the inner product is taken
by update().- SIC_values = None¶
values of the spike induced currents
- V_rest = None¶
resting potential
- Vr = None¶
reset potential (post spike)
- calc_param_dict()[source]¶
The method uses the object’s param_arr attribute and parses this array as a dictionary and saves it as the instance’s param_dict attribute. This dictionary is also returned to the caller.
- compute_X_subthresh(V, Ie)[source]¶
Updates the values of the spike induced currents and then computes
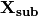 . As explained in the class
docstring, the voltage difference is computed as the inner product
of
. As explained in the class
docstring, the voltage difference is computed as the inner product
of 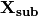 with the parameter vector
with the parameter vector 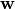 .
.Note
This method can be called even if param_arr has not yet been computed. In fact, the function setup_regression() uses this functionality to compute
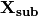 at every time point so that linear regression can then
be easily performed. This practice ensures that the regressed parameters match
the compute_X_subthresh() method without any indexing mismatches. It also
encourages code reuse.
at every time point so that linear regression can then
be easily performed. This practice ensures that the regressed parameters match
the compute_X_subthresh() method without any indexing mismatches. It also
encourages code reuse.
- dt = None¶
time step
- estimate_V_rest(t_wait=1.0)[source]¶
Estimates resting potential of neuron by letting the neuron respond to zero input for a specified amount of time.
Parameters: t_wait – number of seconds to wait for voltage to go to resting state
- is_spiking = None¶
current spiking state of the neuron
- param_arr = None¶
array of subthreshold parameter values
- param_dict = None¶
dictionary of parameter values
- reset()[source]¶
Resets all the spike induced currents to resting state by calling the reset method for all the spike induced currents (eg. see fit_neuron.optimize.sic_lib.ExpDecay_sic.reset()).
- set_param(param_arr)[source]¶
Method to be called after estimate_volt_parameters() has found an optimal set of parameters.
Parameters: param_arr – array of subthreshold parameter values.
- spike()[source]¶
Calls the spike() method of all spike induced current, sets is_spiking to True, and sets the timer of the spike to t_ref.
- t_ref = None¶
refractory period after each spike during which the neuron will have a value of numpy.nan
- t_spike_counter = None¶
A counter used to count down the time during which the neuron spikes. Whenever a spike occurs, its value is set to t_ref.
- update(V=None, Ie=None)[source]¶
This method takes a voltage value and an input current value and returns the value of the voltage at the next time step. If the neuron is not currently is a spiking state, the method will return a float. If the neuron is in a spiking state, the method will return a numpy.nan. value. The values are updated acccording to the object’s dt attribute.
- update_spike_counter()[source]¶
This method, only to be called when the neuron is currently spiking, updates the counter of the spike. Once the neuron has been in a spiking state for a period of time longer than t_ref, the neuron will exit the spiking state by setting is_spiking back to True.
- volt_nonlin_fcn = None¶
voltage nonlinearity function, may be None
- fit_neuron.optimize.subthreshold.estimate_volt_parameters(subthresh_obj, processed_data)[source]¶
Estimates voltage parameters using data provided and stores these as attributes. Does a least squares linear regression of the voltage parameters.
Parameters: - subthresh_obj (Voltage) – subthreshold part of model.
- processed_data (fit_neuron.data.my_data.ProcessedData) – data with the spikes removed.
Returns: array of subthreshold parameters.
The equation we are solving is the following:
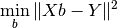
where
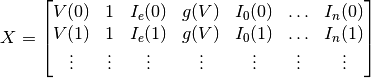
and
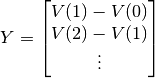
The value of
 that minimizes this expression is the parameter
vector for the subthreshold object.
that minimizes this expression is the parameter
vector for the subthreshold object.
threshold Module¶
threshold¶
Parameter extraction of threshold parameters from voltage clamp data.
- class fit_neuron.optimize.threshold.StochasticThresh(t_bins, volt_adapt_time_const=[], dt=0.0001, thresh_param=None, thresh_param_dict={})[source]¶
Class for the threshold component of a spiking neuron. The main functionality of this class is to determine spike times stochastically.
Parameters: - dt – time step.
- t_bins – a list that defines the
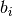 that define indicator functions
that define indicator functions ![I_{[0,b_i]}(t)](_images/math/df973656fcb384f075abc9236bfbc7152cd2a7f1.png) (see below).
(see below). - volt_adapt_time_const – a list that defines the time constants
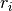 of the voltage chasing currents (see below).
of the voltage chasing currents (see below).
The stochastic neuron has the following hazard rate:
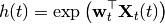
where
![{\bf X}_t (t) = [1,V(t),I_1(t),\hdots,I_m(t),Q_1(t),\hdots,Q_l(t)]^{\top}.](_images/math/05dd85475002ed585ea55d829cec83a64ad87232.png)
where the
![I_i(t) = I_{[0,b_i]}(t)](_images/math/89cbcf6824301bba61402f49d92c15c35fbdee5c.png) parameters are the indicator variables, and
the
parameters are the indicator variables, and
the 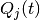 parameters are probability currents which shall be referred to as
voltage chasing currents. These currents give the stochastic spike emission process a component
that adapts to the history of the voltage. The equations used for the voltage chasing currents
are:
parameters are probability currents which shall be referred to as
voltage chasing currents. These currents give the stochastic spike emission process a component
that adapts to the history of the voltage. The equations used for the voltage chasing currents
are: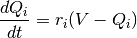
After the neuron spikes, the voltage chasing currents are reset to the value of the voltage immediately following the spike:
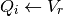
The hazard rate is computed at each time step and compared to a uniformly distributed random number to determine whether the neuron spikes here. The computation of
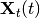 at each time step is done by update_X_arr(), while the inner product with the parameter vector
at each time step is done by update_X_arr(), while the inner product with the parameter vector
 and the random decision of whether a spike occurs or not is taken by update().
and the random decision of whether a spike occurs or not is taken by update().- reset(V=None)[source]¶
This method resets to neuron to a resting state. The spiking history is erased and the the voltage adaption currents are either erased or are set to the current value of the voltage itself.
Parameters: V – value to which voltage chasing currents are reset to
- set_param(param)[source]¶
After the optimization is done, this method allows the final value of the parameter array to be set, and parses this parameter array into a parameter dictionary.
- spike_prob = None¶
current value of the spiking probability
- t_max = None¶
max amount of time during which we care about previous spikes, see self.update
- thresh_param = None¶
these parameters take the internal values and map them to a spike probability
- update(V)[source]¶
Updates inner state and returns True if there is a spike, and False if there is no spike.
- update_X_arr(V)[source]¶
Updates X_arr (the vector with which we do a dot product with the threshold parameters to calculate the spiking probability).
- volt_adapt_currents = None¶
the actual value of the currents which will be an array
- volt_adapt_time_const = None¶
these are the time constants of the voltage chasing parameters
- fit_neuron.optimize.threshold.compute_log_likelihood(X_thresh_list, spike_ind_list, thresh_param)[source]¶
Computes log likelihood of the spike trains given the parameters.
Parameters: - X_thresh_list – list of X_thresh matrices, one array for each sweep
- spike_ind_list – list of spike indices, one array for each sweep
- thresh_param – threshold parameter array
Returns: log likelihood of the time series given parameter array
- fit_neuron.optimize.threshold.estimate_thresh_parameters(subthresh_obj, thresh_obj, raw_data, process_ct=None, max_lik_iter_max=25, thresh_param_init=None, stopping_criteria=0.01)[source]¶
Estimates threshold parameters that fit the raw data, and the particular form of the threshold and subthreshold components of the model.
Parameters: - subthreshold_obj – fit_neuron.optimize.subthreshold.Voltage instance
- thresh_obj – fit_neuron.optimize.threshold.StochasticThresh instance
- raw_data – fit_neuron.data.my_data.RawData instance
- make_lik_iter_max – maximum number of max likelihood iterations
- process_ct – number of processors we want to use to distribute max likelihood; if None then use CPU count.
- stopping_criteria – minimum
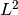 norm of gradient of log likelihood gradient below which we stop optimization.
norm of gradient of log likelihood gradient below which we stop optimization.
Returns: array of threshold parameters
- fit_neuron.optimize.threshold.get_grad_and_hessian((thresh_param, X_cat))[source]¶
Takes a subset of the data and returns gradient and hessian for this subset of the data. This function is called by par_calc_log_like_update and allows this function to work in parallel, map-reduce style. Computes gradient vector as well as Hessian matrix of log likelihood w.r.t. threshold parameters, evaluated at thresh_param. The grad and hess can then be used to update thresh parameters via a Newton-Raphson step.
- fit_neuron.optimize.threshold.max_likelihood(X_thresh_list, spike_ind_list, thresh_init, process_ct=None, iter_max=20, stopping_criteria=0.01)[source]¶
Performs maximum likelihood optimization.
- fit_neuron.optimize.threshold.par_calc_log_like_update(thresh_param, X_cat_split, process_ct)[source]¶
Parallel version of Newton update. This method is called by max_likelihood(). The function splits data into chunks, passes chuncks to different processors, collects the result to obtain the gradient and hessian of the whole time series, then performs Newon update.
 .
.