
The coords module contains classes and functions specifying locations of objects on the sky as well as coordinate converstions and distance computations, including cosmological distance and redshift calculations.
Some of the calculations involved make use of the currently selected cosmology (see astropysics.constants) and hence may not function as expected if a particularly strange cosmology is in use.
Note
Timekeeping/conversion functions are kept in astropysics.obstools, although some are crucial to coordinate systems.
See also
Note
Some functionality in this module makes use of derived versions of the SOFA routines. Use of these derived works requires inclusion of the SOFA license (included in the licenses/SOFA_LICENSE file of the source distribution) and notation indicating how these routines have been modified. In all cases where SOFA-derived routines are used, the routine’s functionality is replicated exactly as the SOFA implementation (barring the possibility of typos), but adapted to the python language.
The coords module is composed of three submodules to make organization clearer. The coordsys module implements classes representing useful coordinate systems in astronomy and a framework to add additional coordinate systems as desired. It also implements standard transformations between the various celestial and terrestrial coordinates (although transformation to local horizontal coordinates is done with methods of astropysics.obstools.Site). ephems implements ephemerides for solar system objects and proper motions. Finally, funcs contains a range of utility functions including cartesian<->spherical and other canonical transforms, as well as cosmological distance calculations. The documentation for each of the sub-modules is described below.
Note
The coords module is composed of submodules that can be accessed seperately. However, they are all also included in the base module. Thus, as an example, astropysics.coords.coordsys.ICRSCoordinates and astropysics.coords.ICRSCoordinates are different names for the same class (ICRSCoordinates). The astropysics.coords.ICRSCoordinates usage is preferred as this allows the internal organization to be changed if it is deemed necessary.
This module contains classes representing coordinates in spatial, celestial, and terrestrial coordinate systems, as well as implementations of transformations between many of the coordinate systems. There are also utility functions for easy-of-use of some of these classes.
The coordinate system framework is designed to allow users to add their own coordinate systems easily, if desired, and implement transformations between theirs and the builtin coordinate systems. This is implemented through the transformation registry static methods of the CoordinateSystem class (e.g. CoordinateSystem.registerTransform()).
A common task might be to convert coordinates from one standard coordinate system to another. The coords module makes this simple:
>>> from astropysics.coords import ICRSCoordinates,GalacticCoordinates
>>> gcoords = ICRSCoordinates('2h34m12.32s',12.3).convert(GalacticCoordinates)
>>> print gcoords
GalacticCoordinates: l=158.558650,b=-43.350066
>>> print '%.3f'%gcoords.l.degrees
158.559
>>> print '%.3f'%gcoords.l.radians
2.767
>>> print gcoords.b.getDmsStr(canonical=True)
-43:21:00.24
Note the initial input composed of an hours,minutes,seconds string input for the RA, and a float for the dec – EquatorialCoordinate objects contain a powerful parsing system that accepts most standard astronomical representations. The resulting GalacticCoordinates object’s coordinates can then be accessed in any of the various ways supported by the AngularCoordinate object.
Warning
Errors are not currently propogated in all coordinate transforms - this will be corrected eventually, but for now you should check to make sure errors propogate for any coordinate transform you want to perform.
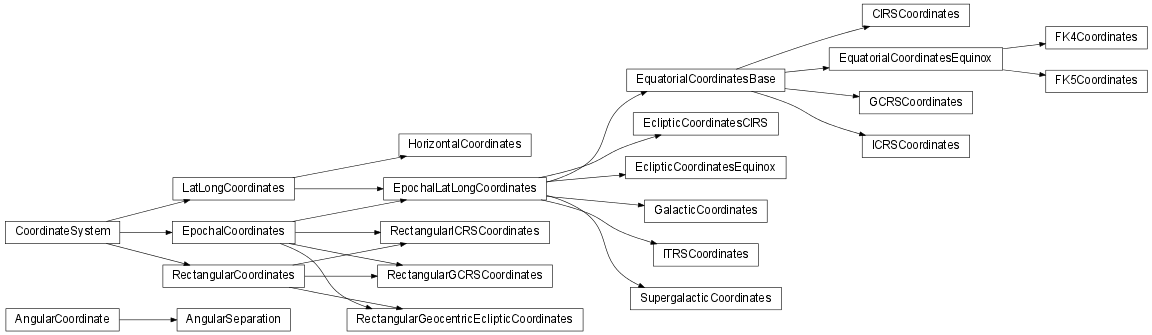
A number of coordinate systems are provided built into astropysics. Most of these have pre-defined standard transformations. The built-in coordinate classes with defined transformation are shown in the diagram below.
![strict digraph "()" {
graph [fontsize=12,
size="12.0, 12.0"
];
FK5Coordinates -> GalacticCoordinates [weight=1.05];
FK5Coordinates -> ICRSCoordinates [weight=1.05];
FK5Coordinates -> FK4Coordinates [weight=1.1];
GalacticCoordinates -> FK5Coordinates [weight=1.05];
GalacticCoordinates -> FK4Coordinates [weight=1.05];
GalacticCoordinates -> SupergalacticCoordinates [weight=1.0];
ICRSCoordinates -> FK5Coordinates [weight=1.05];
ICRSCoordinates -> RectangularICRSCoordinates [weight=1.0];
FK4Coordinates -> FK5Coordinates [weight=1.1];
FK4Coordinates -> GalacticCoordinates [weight=1.05];
EclipticCoordinatesEquinox -> RectangularGeocentricEclipticCoordinates [weight=1.0];
EclipticCoordinatesEquinox -> EquatorialCoordinatesEquinox [weight=1.05];
RectangularGeocentricEclipticCoordinates -> EclipticCoordinatesEquinox [weight=1.0];
RectangularGeocentricEclipticCoordinates -> EclipticCoordinatesCIRS [weight=1.0];
EquatorialCoordinatesEquinox -> EclipticCoordinatesEquinox [weight=1.05];
EquatorialCoordinatesEquinox -> GCRSCoordinates [weight=1.05];
EquatorialCoordinatesEquinox -> CIRSCoordinates [weight=1.05];
EquatorialCoordinatesEquinox -> ITRSCoordinates [weight=1.05];
GCRSCoordinates -> EquatorialCoordinatesEquinox [weight=1.05];
GCRSCoordinates -> RectangularGCRSCoordinates [weight=1.0];
GCRSCoordinates -> CIRSCoordinates [weight=1.0];
RectangularGCRSCoordinates -> GCRSCoordinates [weight=1.0];
RectangularGCRSCoordinates -> RectangularICRSCoordinates [weight=1.0];
CIRSCoordinates -> EquatorialCoordinatesEquinox [weight=1.05];
CIRSCoordinates -> GCRSCoordinates [weight=1.0];
CIRSCoordinates -> EclipticCoordinatesCIRS [weight=1.0];
CIRSCoordinates -> ITRSCoordinates [weight=1.0];
EclipticCoordinatesCIRS -> RectangularGeocentricEclipticCoordinates [weight=1.0];
EclipticCoordinatesCIRS -> CIRSCoordinates [weight=1.0];
RectangularICRSCoordinates -> ICRSCoordinates [weight=1.0];
RectangularICRSCoordinates -> RectangularGCRSCoordinates [weight=1.0];
SupergalacticCoordinates -> GalacticCoordinates [weight=1.0];
ITRSCoordinates -> EquatorialCoordinatesEquinox [weight=1.05];
ITRSCoordinates -> CIRSCoordinates [weight=1.0];
}](../_images/graphviz-876566f908f018c18bb083e6c5976c51884ae10b.png)
A similar diagram can be generated after the user has created and registered custom coordinates and transforms:
from networkx import to_agraph,relabel_nodes,draw_networkx
from astropysics.coords import CoordinateSystem
graph = CoordinateSystem.getTransformGraph()
dotgraph = to_agraph(relabel_nodes(graph,lambda n:n.__name__))
dotgraph.graph_attr.update(dict(size='12.0, 12.0',fontsize=12))
dotgraph.write('mygraph.dot')
draw_networkx(graph)
This will save a graphviz dot file and displaying the graph with matplotlib, showing both builtin and custom-added coordinates and transforms.
Bases: object
A class representing an angular value.
Arithmetic operators can be applied to the coordinate, and will be applied directly to the numerical value in radians. For + and -, two angular coordinates may be used, although for -, an AngularSeparation object will be returned.
The input parser is very adaptable, and can be in any of the following forms for inpt:
if radians is True, this will be interpreted as decimal radians, otherwise, it is in degrees.
A copy of the input object will be created.
The default of 0 will be used.
If sghms is True, the tuple will be interpreted as (hours,min,sec), otherwise, (degrees,min,sec).
If radians is True, this will be cast to a float and used as decimal radians, otherwise, it is in degrees.
The numerical part will be cast to a float and used as degrees.
The numerical part will be cast to a float and used as hours.
The numerical part will be cast to a float and used as radians.
The numerical parts will be treated as hours,minutes, and seconds.
The numerical parts will be treated as degrees,minutes, and seconds.
Sexigesimal form. If sghms is None the presence of a a + or - sign idicates that it should be interpreted as degrees, minutes, and seconds. If the sign is absent, the numerical portions will be treated as hours,min,sec. thewise, if sghms evaluates to True, the numerical parts will be treated as hours,minutes, and seconds, and if sghms evaluates to False, degrees,minutes, and seconds.
| Parameters: |
|
|---|
Examples
>>> from math import pi
>>> ac = AngularCoordinate(2.5)
>>> print ac
+2d30'00.00"
>>> print AngularCoordinate(ac)
+2d30'00.00"
>>> print AngularCoordinate(pi,radians=True)
+180d00.00"
>>> print AngularCoordinate('1.1')
+1d6'00.00"
>>> print AngularCoordinate('1.1',radians=True)
+63d1'31.29"
>>> print AngularCoordinate('12d25m12.5s')
+12d25'12.50"
>>> print AngularCoordinate('3:30:30',sghms=True)
+52d37'30.00"
>>> print AngularCoordinate('3:30:30',sghms=False)
+3d30'30.00"
>>> print AngularCoordinate('-3:30:30',sghms=None)
-3d30'30.00"
>>> print AngularCoordinate('+3:30:30',sghms=None)
+3d30'30.00"
>>> print AngularCoordinate('3:30:30',sghms=None)
+52d37'30.00"
The value of this AngularCoordinate in decimal degrees.
The value of this AngularCoordinate as an (degrees,minutes,seconds) tuple, with degrees and minutes as integers and seconds as a float.
The value of this AngularCoordinate in decimal degrees.
The value of this AngularCoordinate as an (degrees,minutes,seconds) tuple, with degrees and minutes as integers and seconds as a float.
Generates the string representation of this AngularCoordinate as degrees, arcminutes, and arcseconds.
| Parameters: |
|
|---|---|
| Returns: | String representation of this object. |
gets the string representation of this AngularCoordinate as hours, minutes, and seconds
secform is the formatter for the seconds component
sep is the seperator between components - defaults to h, m, and s
canonical forces [+/-]dd:mm:ss.ss , overriding other arguments
Generates the string representation of this AngularCoordinate as hours, minutes, and seconds.
| Parameters: |
|
|---|---|
| Returns: | String representation of this object. |
The value of this AngularCoordinate in decimal hours.
The value of this AngularCoordinate as an (hours,minutes,seconds) tuple, with hours and minutes as integers and seconds as a float.
The value of this AngularCoordinate in decimal hours.
The value of this AngularCoordinate as an (hours,minutes,seconds) tuple, with hours and minutes as integers and seconds as a float.
The value of this AngularCoordinate in decimal radians.
The value of this AngularCoordinate in decimal radians.
The acceptable range of angles for this AngularCoordinate. This can be set as a 2-sequence (lower,upper), or as a 3-sequence (lower,upper,cycle), where cycle can be :
- 0: Angle values are coerced to lie in the range (default for 2-sequence if upper-lower is 360 degrees)
- None: A ValueError will be raised if out-of-range (default for 2-sequence otherwise)
- A positive scalar: Values are coerced in a triangle wave scheme, with the scalar specifying the period. e.g. for the latitude, (-90,90,360) would give the correct behavior)
Bases: astropysics.coords.coordsys.AngularCoordinate
This class represents a separation between two angular coordinates on the unit sphere.
A constructor is available, but the most natural way to generate this object is to use the subtraction (-) operator on two AngularCoordinate objects or two LatLongCoordinates objects.
Input arguments can be either:
Generates a copy of the provided object.
Generates a separation of the provided distance with no starting point.
Computes the separation from the start and end objects, which must be AngularCoordinate objects.
Computes the physical projected separation assuming a given distance.
kwargs are passed into cosmo_z_to_dist() if usez is True.
| Parameters: |
|
|---|---|
| Returns: | a float value for the separation (in pc if redshift is used) |
computes the 3d separation assuming the two points at the ends of this AngularSeparation are at the distances zord1 and zord2.
| Parameters: |
|
|---|---|
| Returns: | a float value for the separation (in pc if redshift is used) |
Bases: astropysics.coords.coordsys.EquatorialCoordinatesBase
Represents an object as equatorial coordinates in the Celestial Intermediate Reference System. This is the post-2000 IAU system for equatorial coordinates that seperates the coordinate system from the dynamically complicated and somewhat imprecisely-defined ideas of the equinox and ecliptic. This system’s fundamental plane is the equator of the Celestial Intermediate Pole (CIP) and the origin of RA is at the Celestial Intermediate Origin (CIO).
Changes to the epoch will result in the coordinates being updated for precession nutation. Nutation currently uses the IAU 2000B model that should be good to ~1 mas. If aberration or annual parallax corrections are necessary, convert to ICRSCoordinates, change the epoch, and then convert back to CIRSCoordinates.
To convert from these coordinates to HorizontalCoordinates appropriate for observed coordinates, site information is necessary. Hence, the transformations from equatorial to horizontal coordinates are performed by the Site class in the obstools module, and attempting to directly convert will raise an TypeError.
Input for equatorial coordinates. Can follow any of the following forms:
Note that the default epoch is 2000 if not otherwise specified. To disable epoch tranformations, set the epoch to None. If scalar values are provided, they are assummed to be degrees.
Latitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Latitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Longitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Longitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Transforms these EquatorialCoordinates to a new epoch using the IAU 2000 precessions from Capitaine, N. et al. 2003 as written in the USNO Circular 179.
alias of RectangularCoordinates
Bases: object
Base class of all coordinate systems. This class also holds the static methods that manage conversion between coordinate systems.
Subclassing
Registers a new transformation type. Transformation types are used to implement particular types of transformations without repeating similar code in each of the actual transformation functions.
The transformation type function (funcorname) will be called as transfunc(trans,coords,toclass), where trans is the output of the actual registered transformation function, coords is the coordinate object that is being converted, and toclass is the target class.
| Parameters: | funcorname (callable or string) – The function to register as the transfromation type function. If a string, the string is taken to be the name to use for the transformation (intended for use as a function decorator). Otherwise, the transformation type name is taken from the name of the function with any intial _ removed. |
|---|---|
| Returns: | The function itself, to allow for use as a decorator. Note that this means that if used as a decorator inside a class, the function will be assigned as an instance method. Alternative, if funcorname is a string, a function to be called on the transformation function will be returned (see second example). |
Examples:
@addTransType
def trans1(trans,coord,tocls):
return tocls(trans*coord.val)
@addTransType('trans1')
def _transfunc(trans,coord,tocls):
return tocls(trans*coord.val)
converts the coordinate system from it’s current system to a new CoordinateSystem object.
| Parameters: | tosys – The new coordinate system class. Should be a subclass of CoordinateSystem . |
|---|---|
| Returns: | A new object of a class determined by tosys |
| Except: | raises NotImplementedError if conversion is not present |
Deletes the transformation function to go from fromclass to toclass.
Returns the transformation function to go from fromclass to toclass.
Returns a networkx <http://networkx.lanl.gov/> DiGraph object representing a graph of the registered coordinate systems and the transformations between them.
| Raises ImportError: | |
|---|---|
| If networkx is not installed. | |
Determines the transformation path from one coordinate system to another for use with convert().
| Parameters: |
|
|---|---|
| Returns: | A list of coordinate classes with the shortest path from fromsys to tosys (including fromsys and tosys) or a callable with the transformation if a single-step direct transformation is available |
| Raises NotImplementedError: | |
If no path can be found. |
|
Returns a list of 2-tuples (fromclass,toclass) of all the coordinate system combinations that have registered transformation functions.
Returns a list of classes that can be transformed from the supplied class.
Returns a list of classes that can be transformed to the supplied class.
Register a function to transform coordinates from one system to another.
The transformation function is called is func(fromobject) and should return a new object of type toclass. If called with no arguments, the function should raise a NotImplementedError or behave in a manner defined in subclasses (see e.g. LatLongCoordinates). If transtype is not None, the output of the transformation function is filered through the function applied for that type using astropysics.CoordinateSystem.addTransType() .
If the transformation function func is None, the function is taken to be a decorator, and if it is a method of a subclass of CoordinateSystem, fromclass or toclass may be the string ‘self’ . In this case, the function will use the class itself as the from or to class. The function will then be treated as a static method (e.g. it should not have self as the first argument).
| Parameters: |
|
|---|
Examples:
class MyCoordinates(CoordinateSystem):
...
class YourCoordinates(CoordinateSystem):
...
def transformer(mycooobj):
...
return yourcoordobj
CoordinateSystem.registerTransform(MyCoordinates,YourCoordinates,transformer)
class TheirCoordinates(CoordinateSystem):
@CoordinateSystem.registerTransform(MyCoordinates,'self')
@classmethod
def fromMy(cls,mycoordinates):
...
return theircoordobj
Bases: astropysics.coords.coordsys.EpochalLatLongCoordinates
Ecliptic Coordinates (beta, lambda) such that the fundamental plane passes through the ecliptic at the current epoch.
Note that because the concept of the ecliptic can be complicated or even ill-defined, ecliptic coordinates is astropysics are simply defined as tied to a particular set of equatorial coordinates with a given obliquity model. For EclipticCoordinatesCIRS, the equatorial coordinates are CIRSCoordinates with obliquity given by the IAU 2006 obliquity model (see obliquity())
See the associated attribute docstrings for the meaning of the inputs.
Latitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Latitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Longitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Longitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Bases: astropysics.coords.coordsys.EpochalLatLongCoordinates
Ecliptic Coordinates (beta, lambda) such that the fundamental plane passes through the ecliptic at the current epoch.
Note that because the concept of the ecliptic can be complicated or even ill-defined, ecliptic coordinates is astropysics are simply defined as tied to a particular set of equatorial coordinates with a given obliquity model. For EclipticCoordinatesEquinox, the equatorial coordinates are EquatorialCoordinatesEquinox with obliquity given by the IAU 1980 obliquity model (see obliquity())
See the associated attribute docstrings for the meaning of the inputs.
Latitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Latitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Longitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Longitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Bases: astropysics.coords.coordsys.CoordinateSystem
A base class for CoordinateSystem classes that have changeable epochs associated with them.
Subclassing
Subclasses must implement these methods:
- __init__() from CoordinateSystem
- transformToEpoch() – see the method’s entry for details.
Furthermore, subclasses should set julianepoch to determine if they are Julian or Besselian.
Epoch for this coordinate as a float.
Setting with the string ‘now’ will set the epoch to the time at the moment the command is executed.
If set, this coordinate will be transformed to the new epoch, unless the current Epoch is None, in which case the epoch will be set with no transformation. If transformation is not desired, first set the epoch to None, and then set to the new epoch.
Julian vs. Besselian is determined by the julianepoch attribute.
A string representation of the epoch of this object with a J or B prefixed for julian or besselian epochs.
Julian Date of the epoch for this object.
If True, the epoch is Julian, otherwise, Besselian
Modified Julian Date of the epoch for this object.
Subclasses should implement this method to transform their coordinates to a new epoch. At the end of this method after the necessary data transformations are performed, subclasses should call EpochalCoordinates.transformToEpoch(newepoch).
Bases: astropysics.coords.coordsys.LatLongCoordinates, astropysics.coords.coordsys.EpochalCoordinates
A Coordinate system where the coordinates change as a function of time. The origin and orientation of some coordinate systems are tied to the motion of the Earth and Solar System and hence most be updated as time passes.
In general this only accounts for epoch-related changes in its own coordinate system. If (for example) one has a ITRSCoordinates coordinate, changing the epoch only updates for polar motion. To properly update all epoch-related such as precession/nutation and earth rotation, the coordinate should be transformed to ICRSCoordinates , update the epoch, and transform back to TIRSCoordinates .
See the associated attribute docstrings for the meaning of the inputs.
Converts the coordinate system from it’s current system to a new CoordinateSystem object possibly with optimizations for matrix-based transformation of LatLongCoordinates objects.
Warning
The transformation optimizations used if optimize is True are only correct if the conversion matricies are independent of the coordinate values themselves (e.g. are linear and epoch-independent). Examples that are good for optimization include FK4->FK5->ICRS (all are epoch-independent).
In the future, this system will be smarter about knowing when it is safe to optimize, but for now, only use it if you’re sure it will work correctly.
| Parameters: |
|
|---|---|
| Returns: | A new object of a class determined by tosys |
| Except: | raises NotImplementedError if converters are not present |
Latitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Latitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Longitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Longitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Bases: astropysics.coords.coordsys.EpochalLatLongCoordinates
This object represents an angular location on the unit sphere, specified in right ascension and declination. Some of the subclasses are not strictly speaking equatorial, but they are close, or are tied to the equatorial position of a particular epoch.
This is a superclass for all other Equatorial Coordinate systems - particular reference systems implement the transformToEpoch() method. See the docstring for EpochalLatLongCoordinates for subclassing suggestions.
Input for equatorial coordinates. Can follow any of the following forms:
Note that the default epoch is 2000 if not otherwise specified. To disable epoch tranformations, set the epoch to None. If scalar values are provided, they are assummed to be degrees.
Converts the coordinate system from it’s current system to a new CoordinateSystem object possibly with optimizations for matrix-based transformation of LatLongCoordinates objects.
Warning
The transformation optimizations used if optimize is True are only correct if the conversion matricies are independent of the coordinate values themselves (e.g. are linear and epoch-independent). Examples that are good for optimization include FK4->FK5->ICRS (all are epoch-independent).
In the future, this system will be smarter about knowing when it is safe to optimize, but for now, only use it if you’re sure it will work correctly.
| Parameters: |
|
|---|---|
| Returns: | A new object of a class determined by tosys |
| Except: | raises NotImplementedError if converters are not present |
Latitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Latitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Longitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Longitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Bases: astropysics.coords.coordsys.EquatorialCoordinatesBase
Represents an object in mean geocentric apparent equatorial coordinates, using the pre-IAU2000 systems where the plane of the ecliptic is the fundamental plane and the origin is at the equinox of date (as set by epoch).
Changes to the epoch will result in the coordinates being updated for precession, but not nutation, nor annual abberation. Neither are planned by the primary author of this package, as IAU 2000 recommends using only CIO-based systems, but if someone actually wants equinox-based nutation, feel free to implement it and pass it along.
To convert from these coordinates to HorizontalCoordinates appropriate for observed coordinates, site information is necessary. Hence, the transformations from equatorial to horizontal coordinates are performed by the Site class in the astropysics.obstools module, and attempting to directly convert will raise a TypeError.
Input for equatorial coordinates. Can follow any of the following forms:
Note that the default epoch is 2000 if not otherwise specified. To disable epoch tranformations, set the epoch to None. If scalar values are provided, they are assummed to be degrees.
Latitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Latitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Longitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Longitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Transforms these EquatorialCoordinates to a new epoch using the IAU 2000 precessions from Capitaine, N. et al. 2003 as written in the USNO Circular 179.
Bases: astropysics.coords.coordsys.EquatorialCoordinatesEquinox
Equatorial Coordinates fixed to the FK4 reference system. Note that this implementation does not correct for the elliptic terms of aberration as of yet.
Epoch is Besselian.
Input for FK4 coordinates. Can follow any of the following forms:
The epoch of FK4 coordinates defaults to B1950.
Latitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Latitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Longitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Longitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Transforms these EquatorialCoordinates to a new epoch. Uses the method of Newcomb (pre-IAU1976) to compute precession.
Bases: astropysics.coords.coordsys.EquatorialCoordinatesEquinox
Equatorial Coordinates fixed to the FK5 reference system.
Input for equatorial coordinates. Can follow any of the following forms:
Note that the default epoch is 2000 if not otherwise specified. To disable epoch tranformations, set the epoch to None. If scalar values are provided, they are assummed to be degrees.
Latitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Latitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Longitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Longitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Transforms these EquatorialCoordinates to a new epoch. Uses the algorithm resolved by the IAU in 1976 as written in Meeus, as well as Lieske, J.H. 1979.
According to SOFA, this for becomes less valid at the following levels:
< 0.1”
< 1”
< 3”
> 10”
> 100”
> 1000”
Bases: astropysics.coords.coordsys.EquatorialCoordinatesBase
Geocentric Celestial Reference System equatorial coordinates. The orientation of this coordinates is fixed to the ICRS orientation, but with origin at the earth geocenter.
Warning
Abberation of starlight not yet included in transforms.
Input for equatorial coordinates. Can follow any of the following forms:
Note that the default epoch is 2000 if not otherwise specified. To disable epoch tranformations, set the epoch to None. If scalar values are provided, they are assummed to be degrees.
Latitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Latitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Longitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Longitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Transforms from the current epoch to a new epoch by converting to ICRS and back again in the new epoch.
Bases: astropysics.coords.coordsys.EpochalLatLongCoordinates
See the associated attribute docstrings for the meaning of the inputs.
Latitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Latitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Longitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Longitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Galactic coordinates are nominally inertial, although the definition is a bit unclear in that regard.
Bases: astropysics.coords.coordsys.LatLongCoordinates
This object represents an angular location on the unit sphere, with the north pole of the coordinate position fixed to the local zenith
To convert from other Coordinate types to horizontal positions, see astropysics.obstools.Site, as site information is required for these corrections
See the associated attribute docstrings for the meaning of the inputs.
Latitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Latitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Longitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Longitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Bases: astropysics.coords.coordsys.EquatorialCoordinatesBase
Equatorial Coordinates tied to the International Celestial Reference System (ICRS). Strictly speaking this is not an Equatorial system, as it is an inertial frame that only aligns with Earth’s equator at J2000, but it is nearly an equatorial system at J2000.
Note
Technically, this is actually the Barycentric Celestial Referense System (BCRS), distringuished from ICRS by having acounted for space motion. In astropysics, instead, space motion is already accounted for by using a astropysics.coords.ephems.EphemerisObject object, which yields coordinates (often ICRSCoordinates) at the epoch of observation.
Warning
Abberation of starlight is not yet implemented in transformations to/from ICRS.
Input for equatorial coordinates. Can follow any of the following forms:
Note that the default epoch is 2000 if not otherwise specified. To disable epoch tranformations, set the epoch to None. If scalar values are provided, they are assummed to be degrees.
Latitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Latitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Frame bias matrix such that vJ2000 = B*vICRS .
Longitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Longitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
ICRS is an inertial frame, so no transformation is necessary
Bases: astropysics.coords.coordsys.EpochalLatLongCoordinates
Coordinates based on the International Terrestrial Reference System. The particular implementation here assumes ITRS matches the WGS84 coordinates (used by GPS) - for astronomical purposes, this is a perfectly good assumption.
Epoch transformations in this system only adjust for polar motion - to account for earth rotation, transform back to CIRSCoordinates or EquatorialCoordinatesEquinox, change the epoch, then transfrom back to ITRSCoordinates.
Because polar motion is not fully predictable, a number of methods are available for approximating it. To choose a method, set the ITRSCoordinates.polarmotion class attribute – this will also affect all future transformations to ITRSCoordinates from other coordinate systems. The following are valid values:
- None
Assumes the pole locations are fixed to the CIP at all times, aside from the tiny effect of s’ (the TIO-CIO shift).
- A 2-tuple of callables (xp,yp)
They will be called as xp(epoch) and yp(epoch) and the result will be assumed to give the x and y coordinates of the poles in the CIP frame.
Note
The transformations from CIRS and Equinox systems to ITRS technically involve converting to TIRS (the Terrestrial Intermediate Reference System), distinguished from ITRS by no polar motion correction. While there is no class explicitly representing TIRS, ITRS with epoch set to None is equivalent to TIRS.
See the associated attribute docstrings for the meaning of the inputs.
Latitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Latitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Longitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Longitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Technique of computing poles (see ITRSCoordinates documentation)
Transforms these ITRSCoordinates to a new epoch, adjusting the coordinate values for polar motion.
Bases: astropysics.coords.coordsys.CoordinateSystem
This object represents an angular location on a sphere as represented in spherical coordinates with a latitude and longitude, and optionally a distance. Subclasses specify details such as transformations or epochs.
A LatLongCoordinate system is designed to use the transformation type (see CoordinateSystem.addTransType()) ‘smatrix’. Thus, if the transformation between two LatLongCoordinate subclasses can be represented as a unitary matrix operating on position vectors on the unit sphere, the transformation function can be written as:
@CoordinateSystem.registerTransform(InLLCoords,OutLLCoords,transtype='smatrix')
def transform(incoord):
... compute the elements of a 3x3 transformation matrix...
return np.mat([[a,b,c],[d,e,f],[g,h,i]])
Subclassing
Subclasses of LatLongCoordinates can have the class attribute _longlatnames_ as a 2-tuple of strings (longname,latname), with names for the two coordinates, e.g. (‘ra’,’dec’). They can also include the _longrange_ attribute, which specifies the range of valid values for the longitude (latitude is always -90 to 90 degrees), or None to place no restriction. See CoordinateSystem for additional subclassing information.
See the associated attribute docstrings for the meaning of the inputs.
Converts the coordinate system from it’s current system to a new CoordinateSystem object possibly with optimizations for matrix-based transformation of LatLongCoordinates objects.
Warning
The transformation optimizations used if optimize is True are only correct if the conversion matricies are independent of the coordinate values themselves (e.g. are linear and epoch-independent). Examples that are good for optimization include FK4->FK5->ICRS (all are epoch-independent).
In the future, this system will be smarter about knowing when it is safe to optimize, but for now, only use it if you’re sure it will work correctly.
| Parameters: |
|
|---|---|
| Returns: | A new object of a class determined by tosys |
| Except: | raises NotImplementedError if converters are not present |
Parallax distance to object in AU, or None to assume infinity. Set as either a float, a 2-tuple (distance,distance_error), or a no-argument callable that returns such a tuple. Getter always returns 2-tuple or None.
Parallax distance to object in parsecs, or None to assume infinity. Set as either a float, a 2-tuple (distance,distance_error), or a no-argument callable that returns such a tuple. Getter always returns 2-tuple or None.
Latitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Latitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Latitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Latitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Longitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Longitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Longitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Longitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Applies the supplied unitary rotation matrix to these coordinates.
| Parameters: |
|
|---|---|
| Returns: | (lat,long) as decimal radians after the transformation matrix is applied or (lat,long,laterr,longerr) if errors are nonzero |
Bases: astropysics.coords.coordsys.CoordinateSystem
Rectangular/Cartesian Coordinates in three dimensions. Coordinates are accessed via the attributes x, y, and z.
The Length of this coordinate’s vector e.g. distance from the origin. If set, the direction will be preserved but the vector will be scaled to the provided value.
x cartesian coordinate value
y cartesian coordinate value
z cartesian coordinate value
Bases: astropysics.coords.coordsys.RectangularCoordinates, astropysics.coords.coordsys.EpochalCoordinates
Rectangular coordinates aligned to the GCRS with origin at the Earth geocenter. The positive z-axis points to the north celestial pole and the positive x-axis points down the (0,0) point of the equatorial GCRS (and thus, also ICRS).
The coordinates at this location are actually an “Astrometric place” - the actual location relative to the geocenter. This is disctinct from GCRSCoordinates in that GCRSCoordinates includes aberration and light deflection, while RectangularGCRSCoordinates does not.
Note
Units for the coordinates are specified via the unit attribute. When converting from GCRSCoordinates, distances default to AU if less than 1000 AU, otherwise, pc. If a distance is not present, the default distance is 1 (unspecified unit).
The unit for these coordinates. Must be ‘au’, ‘pc’, or None - setting to anything else will raise a ValueError. If not None, setting to a new unit will convert the values from AU to pc or vice versa.
Bases: astropysics.coords.coordsys.RectangularCoordinates, astropysics.coords.coordsys.EpochalCoordinates
Rectangular coordinates oriented so that the x-y plane lies in the plane of the ecliptic at the specified epoch. Distances are in AU. Origin is at the center of mass of the Earth.
Note that the epoch should not be set directly - if precession is desired desired, convert to an Ecliptic coordinate system, do the precession, and convert back.
Bases: astropysics.coords.coordsys.RectangularCoordinates, astropysics.coords.coordsys.EpochalCoordinates
Rectangular coordinates aligned to the ICRS with origin at the solar system barycenter. The positive z-axis points to the north celestial pole and the positive x-axis is along with the (0,0) point of the equatorial ICRS.
Note
Units for the coordinates are specified via the unit attribute. When converting from ICRSCoordinates, distances default to AU if less than 1000 AU, otherwise, pc. If a distance is not present, the default distance is 1 (unspecified unit).
The unit for these coordinates. Must be ‘au’, ‘pc’, or None - setting to anything else will raise a ValueError. If not None, setting to a new unit will convert the values from AU to pc or vice versa.
Bases: astropysics.coords.coordsys.EpochalLatLongCoordinates
See the associated attribute docstrings for the meaning of the inputs.
Latitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Latitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Longitude of this object as a AngularCoordinate object. May be set using any valid input form for AngularCoordinate.
Longitude error for this object as a AngularSeparation object. May be set using any valid input form for AngularSeparation.
Supergalactic coordinates are nominally inertial, although the definition is a bit unclear in that regard.
Convinience function to convert a angular coordinate string to a decimal value.
| Parameters: |
|
|---|---|
| Returns: | Decimal value in radians or degrees |
converts a sequence of position objects into an array of coordinates.
coords determines the order of the output coordinates - it can be a comma-seperated list of coordinate names or if ‘auto’, it will be ‘lat,long’ for all coordinate systems except for Equatorial, which will use ‘ra,dec’
if degrees is True, returned arrays are in degrees, otherwise radians
This module contains tools and utilities for computing ephemerides and physical locations of solar system objects, as well as proper motion calculations for extrasolar objects.
See also
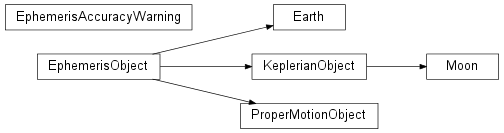
Bases: astropysics.coords.ephems.EphemerisObject
Earth position (and velocity) relative to solar system barycenter. Adapted from SOFA fits generated from DE405 solar system model. Outputs astropysics.coords.coordsys.RectangularICRSCoordinates objects.
Computes and returns the velociy of the Earth relative to the solar system barycenter.
| Params jd: | The julian date at which to compute the velocity, or None to use the jd attribute. |
|---|---|
| Params bool kms: | |
| If True, velocities are returned in km/s, otherwise AU/yr. | |
| Returns: | vx,vy,vz in km/s if kms is True, otherwise AU/yr. |
Bases: exceptions.Warning
Class for warnings due to Ephemeris accuracy issues
Bases: object
This class is the superclass of objects that change sky coordinates over time.
Subclassing
| Params name: | The name of the object. |
|---|---|
| Params validjdrange: | |
| Sets the jd range over which this method is valid as (minjd,maxjd). Trying to get something outside will result in an :exc:EphemerisAccuracyWarning warning. minjd or maxjd can be None to indicate no bound. | |
Computes and returns the instantaneous velocity for this object at the time given by the jd attribute’s value.
| Returns: | The current velocity of this object. The exact type is not specified, but it should be something that can be added to the coordinates that are returned when the object is called. |
|---|---|
| Raises NotImplementedError: | |
| If velocities are not implemented for this class. | |
Julian Date at which to calculate the orbital elements. Can be set either as a scalar JD, ‘now’, datetime.datetime object or a compatible tuple.
The name of the object.
The range of jds over which these ephemerides are valid. Returns a 2-tuple (minjd,maxjd), either of which can be None to indicate no bound.
Bases: astropysics.coords.ephems.EphemerisObject
An object with Keplerian orbital elements.
The following orbital elements are available for the current value of jd as read-only properties:
Additional read only properties derived from the orbital elements include:
Keywords should be the names of orbital elements. Orbital elements can be a callable f(T) that returns the orbital element, where T is the Julian century from J2000. Otherwise, it must be a sequence giving polynomial coefficients of T, specified in increasing power (i.e. constant term first).
The orbital elements a,:attr:e, i, and Lan must be specified, as must either L and Lp or ap and M
Three additional keywords can be supplied:
| Params outcoords: | |
|---|---|
| The coordinate class that should be used as the output. Should be a astropysics.coords.coordsys.CartesianCoordinates subclass, and the origin will be taken as the center of the Keplerian orbit. Defaults to astropysics.coords.coordsys.RectangularCoordinates. | |
| Params outtransfunc: | |
| A function that maps the coordinates from the standard coordinate system (where the x-y plane is the plane of reference) to a system matching the type specified by outcoords. The function should have the signature f(x,y,z,jd) and return (xp,yp,zp). It can also be None to perform no trasnformation. Defaults to None. | |
| Params Etol: | Tolerance for eccentric anomaly (see Etol). Defaults to None. |
Any other keywords will be passed into the constructor for EphemerisObject.
| Raises TypeError: | |
|---|---|
| If necessary orbital elements are missing. | |
Desired accuracy for iterative calculation of eccentric anamoly (or
true anomaly) from mean anomaly. If None, default tolerance is used
(1.5e-8), or if 0, an analytic approximation will be used (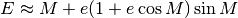 ). This approximation can be 10x faster to
compute but fails for e close to 1.
). This approximation can be 10x faster to
compute but fails for e close to 1.
The mean longitude in degrees.
The longitude of the ascending node in degrees.
The longitude of the pericenter in degrees.
The mean anomaly in degrees.
Orbital period (if gravitational parameter GM=1).
The semi-major axis.
The argument of the pericenter in degrees.
Current distance from focus of attraction to object.
Distance from focus of attraction at apocenter.
Distance from focus of attraction at pericenter.
The eccentricity in radians.
Computes the phase of this object. The phase is computed as viwed from viewobj if illuminated by illumobj
| Parameters: |
|
|---|---|
| Returns: | The phase of the object as a float where 0 is new and 1 is full. |
The orbital inclination in degrees.
Bases: astropysics.coords.ephems.KeplerianObject
A KeplerianObject for Earth’s moon based on the model of Simon et al. 1994. The osculating elements for the “1992 values” are used to compute the location. The output coordinates are astropysics.coords.coordsys.RectangularGCRSCoordinates.
Computes the phase of the Moon. This is computed as viewed from the Earth and illuminated by the Sun if viewobj and illumobj are None - otherwise, see KeplerianObject.getPhase() for the meaning of the parameters.
| Returns: | A float where 1 is full and 0 is new. |
|---|
Bases: astropysics.coords.ephems.EphemerisObject
An object with linear proper motion relative to a specified epoch.
| Parameters: |
|
|---|
Declination at the current jd in degrees.
Distance at the current jd in parsecs.
Proper motion in right ascention in arcseconds. This is distinguished from dra in that it is multiplied by cos(dec0) to produce a true proper motion component.
RA at the current jd in degrees.
Computes the earth’s position and velocity at a given julian date.
Output coordinates are aligned to GCRS/ICRS so that +z is along the spherical GCRS pole and +x points down the spherical GCRS origin.
Adapted from SOFA function epv00.c from fits to DE405, valid from ~ 1900-2100.
| Parameters: | |
|---|---|
| Returns: | 2 3-tuples (x,y,z),(vx,vy,vz) where x,y, and z are GCRS-aligned positions in AU, and vx,vy, and vz are velocities in km/s if kms is True, or AU/yr. |
Retrieves an EphemerisObject object or computes the coordinates for a solar system object.
| Parameters: |
|
|---|---|
| Returns: | A subclass of EphemerisObject if jds is None, or the appropriate coordinate object (or objects) as detailed in EphemerisObject.__call__() if jds is not None. |
Returns a list of objects that can be returned by get_solar_system_object().
Sets the type of ephemerides to use. Must be ‘keplerian’ for now.
This module contains functions for coordinate transforms and coordinate system calculations. It also includes distance-related calculations, including distances in expanding cosmologies.
Converts an observed angular size (in arcsec or as an AngularSeparation object) to a physical size.
| Parameters: |
|
|---|
kwargs are passed into cosmo_z_to_dist() if usez is True.
| Returns: | A scalar value for the physical size (in pc if redshift is used, otherwise in zord units) |
|---|
Converts three arrays in 3D rectangular Cartesian coordinates to cylindrical polar coordinates.
| Parameters: |
|
|---|---|
| Returns: | Cylindrical coordinates as a (rho,theta,z) tuple (theta increasing from +x to +y, 0 at x-axis). |
Converts arrays in 2D rectangular Cartesian coordinates to polar coordinates.
| Parameters: |
|
|---|---|
| Returns: | (r,theta) where theta is measured from the +x axis increasing towards the +y axis |
Converts three arrays in 3D rectangular cartesian coordinates to spherical polar coordinates.
Note that the spherical coordinates are in physicist convention such that (1,0,pi/2) is x-axis.
| Parameters: |
|
|---|---|
| Returns: | arrays (r,theta,phi) |
Converts from colatitude/inclination (i.e. “theta” in physicist convention) to latitude (i.e. 0 at the equator).
| Parameters: |
|
|---|---|
| Returns: | latitude |
Convert a distance to a redshift. See cosmo_z_to_dist() for meaning of parameters. Note that if d is None, the maximum distance will be returned.
Calculates the hubble constant as a function of redshift for the current astropysics.constant.Cosmology .
| Parameters: |
|
|---|---|
| Returns: | Hubble constant for the given redshift, or (H,upper_error,lower_error) if zerr is not None |
Calculates the cosmolgical distance to some object given a redshift. Note that this uses H0,omegaM,omegaL, and omegaR from the current astropyscs.constants.Cosmology – if any of those do not exist in the current cosmology this will fail.
The distance type can be one of the following:
| Parameters: |
|
|---|---|
| Returns: | Distance of type selected by disttype in above units or normalized as controlled by normed parameter. If zerr is not None, the output is (z,zupper,zlower), otherwise just z. |
Examples
In these examples we are assuming the WMAP7 BAOH0 cosmological parameters.
>>> from astropysics.constants import choose_cosmology
>>> cosmo = choose_cosmology('wmap7baoh0')
>>> '%.6f'%cosmo_z_to_dist(0.03)
'126.964723'
>>> '%.6f'%cosmo_z_to_dist(0.2)
'815.469170'
>>> '%.6f'%cosmo_z_to_dist(0.2,disttype=1)
'978.563004'
>>> '%.6f'%cosmo_z_to_dist(0.2,disttype='luminosity')
'978.563004'
>>> '%.6f'%cosmo_z_to_dist(0.2,disttype='angular')
'679.557642'
>>> '%.3f'%cosmo_z_to_dist(1,disttype='lookback')
'7.789'
>>> '%.2f'%cosmo_z_to_dist(0.5,disttype='distmod')
'42.27'
>>> '%.6f'%cosmo_z_to_dist(0.2,disttype='angular',normed=True)
'0.382326'
>>> '%.6f'%cosmo_z_to_dist(0.8,disttype='angular',normed=True)
'0.879027'
>>> '%.6f'%cosmo_z_to_dist(1.64,disttype='angular',normed=True)
'1.000000'
>>> '%.6f'%cosmo_z_to_dist(2.5,disttype='angular',normed=True)
'0.956971'
Converts three arrays in cylindrical polar coordinates to 3D rectangular Cartesian coordinates.
| Parameters: |
|
|---|---|
| Returns: | Cartesian coordinates as an (x,y,z) tuple. |
Earth Rotation Angle (ERA) for a given Julian Date.
| Parameters: |
|
|---|---|
| Returns: | ERA or an array of angles (if jd is an array) |
Computes equation of the equinoxes GAST-GMST. That is, the difference between GMT computed using the mean equinox instead of the true equinox (i.e. including nutation).
| Parameters: | jd (scalar or array-like) – The Julian Date or a sequence of JDs. |
|---|---|
| Returns: | the equation of the equinoxes for the provided date in hours. |
Computes the equation of the origins ERA - GAST (ERA = Earth Rotation Angle, GAST = Greenwich Apparent Sidereal Time). This quantity is also the difference in RA between the Celestial Intermediate Origin and the Equinox.
| Parameters: | jd (scalar or array-like) – The Julian Date or a sequence of JDs. |
|---|---|
| Returns: | the equation of the origins for the provided date in hours. |
Converts a geocentric latitude to a geographic/geodetic latitude.
| Parameters: | geoclat – An astropysics.coords.AngularCoordinate object (or arguments to create one) or an angle in degrees for the geocentric latitude. |
|---|---|
| Returns: | An astropysics.coords.AngularCoordinate object with the geographic latitude. |
Converts a geographic/geodetic latitude to a geocentric latitude.
| Parameters: | geoglat – An astropysics.coords.AngularCoordinate object (or arguments to create one) or an angle in degrees for the geographic latitude. |
|---|---|
| Returns: | An astropysics.coords.AngularCoordinate object with the geocentric latitude. |
Computes the Greenwich Sidereal Time for a given Julian Date.
| Parameters: |
|
|---|---|
| Returns: | GMST or GAST in hours or an array of times (if jd is an array) |
See also
equation_of_the_equinoxes(), USNO Circular 179, http://www.usno.navy.mil/USNO/astronomical-applications/astronomical-information-center/approx-sider-time, IERS Technical Note No. 32 (esp. 5.10 Method (2B)), and SOFA functions iauGmst00 and iauGst00b
converts from latitude (i.e. 0 at the equator) to colatitude/inclination (i.e. “theta” in physicist convention).
Match one pair of coordinate arrays to another within a specified tolerance (eps).
Distance is determined by the cartesian distance between the two arrays, implying the small-angle approximation if the input coordinates are spherical. Units are arbitrary, but should match between all coordinates (and eps should be in the same units)
| Parameters: |
|
|---|---|
| Returns: | See mode for a description of return types. |
Examples
>>> from numpy import array
>>> ra1 = array([1,2,3,4])
>>> dec1 = array([0,0,0,0])
>>> ra2 = array([4,3,2,1])
>>> dec2 = array([3.5,2.5,1.5,.5])
>>> match_coords(ra1,dec1,ra2,dec2,1)
(array([ True, False, False, False], dtype=bool), array([False, False, False, True], dtype=bool))
Match a set of coordinates to their nearest neighbor(s) in another set of coordinates.
| Parameters: |
|
|---|---|
| Returns: | (seps,ind2) where both are arrays matching the shape of c1. ind2 is indecies into c2 to find the nearest to the corresponding c1 coordinate, and seps are the distances. |
Computes the obliquity of the Earth at the requested Julian Date.
| Parameters: |
|
|---|---|
| Returns: | mean obliquity in degrees (or array of obliquities) |
See also
computes the projected separation for a list of points in galacto-centric coordinates as seen from a point offset (an [[x,y,z]] 2-sequence)
spherical determines if the inputs are spherical coords or cartesian. If it is ‘degrees’, spherical coordinates will be used, converting from degrees to radians
Converts a physical size (in pc) to an observed angular size (in arcsec or as an AngularSeparation object if objout is True)
if usez is True, zord is interpreted as a redshift, and cosmo_z_to_dist is used to determine the distance, with kwargs passed into cosmo_z_to_dist otherwise, zord is taken directly as a angular diameter distance (in pc) and kwargs should be absent
| Parameters: |
|
|---|---|
| Type: | bool |
kwargs are passed into cosmo_z_to_dist() if usez is True.
| Returns: | The angular size in acsec, or an AngularSeparation object if objout is True. |
|---|
Converts arrays in 2D polar coordinates to rectangular cartesian coordinates.
Note that the spherical coordinates are in physicist convention such that (1,0,pi/2) is x-axis.
| Parameters: |
|
|---|---|
| Returns: | arrays (x,y) |
Convert a sequence of string coordinate specifiers to decimal degree arrays.
Two input forms are accepted:
In this form, rastrs and decstrs are sequences of strings with the RA and Dec, respectively.
In this form, radecstrs is a sequence of strings in any form accepted by the EquatorialCoordinatesBase constructor. (typically canonical from like 17:43:54.23 +32:23:12.3)
| Returns: | (ras,decs) where ras and decs are ndarrays specifying the ra and dec in decimal degrees. |
|---|
Computes a matrix of the separation between each of the components of the first dimension of an array. That is, A[i,j] = v[i]-w[j].
| Parameters: |
|
|---|---|
| Returns: | Separation matrix with dimension nXmX(whatever the remaining dimensions are) |
See also
scipy.spatial.distance, in particular the scipy.spatial.distance.pdist() function. It is much more efficient and flexible at computing distances if individual components and sign information is unnecessary.
Compute the full 3D separation between two objects at distances d1 and d2 and angular positions pos1 and pos2 (LatLongCoordinates objects, or an argument that will be used to generate a EquatorialCoordinatesEquinox object)
| Parameters: |
|
|---|
>>> from coordsys import LatLongCoordinates
>>> p1 = LatLongCoordinates(0,0)
>>> p2 = LatLongCoordinates(0,10)
>>> '%.10f'%sky_sep_to_3d_sep(p1,p2,20,25)
'6.3397355613'
>>> '%.10f'%sky_sep_to_3d_sep('0h0m0s +0:0:0','10:20:30 +0:0:0',1,2)
'2.9375007333'
Converts arrays in 3D spherical polar coordinates to rectangular cartesian coordinates.
Note that the spherical coordinates are in physicist convention such that (1,0,pi/2) is x-axis.
| Parameters: |
|
|---|---|
| Returns: | arrays (x,y,z) |