Tutorial¶
Proper list-colourings of simple graphs¶
Basic list-colouring – complete graph on 4 vertices¶
Let’s start with a simple example. We take the complete graph 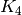 on 4 vertices. and assign each vertex the list of colours
on 4 vertices. and assign each vertex the list of colours 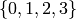 .
We use networkx to build our graph structure.
.
We use networkx to build our graph structure.
>>> import networkx
>>> G = networkx.complete_graph(4)
We’re going to find a proper colouring of this graph when the colours at every
vertex are chosen from the list 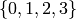 . So, we have to build the
appropriate map from vertices to lists. An ordinary Python dictionary suffices
for such a map.
. So, we have to build the
appropriate map from vertices to lists. An ordinary Python dictionary suffices
for such a map.
>>> L = dict([(node, range(4)) for node in G.nodes()])
>>> L
{0: [0, 1, 2, 3], 1: [0, 1, 2, 3], 2: [0, 1, 2, 3], 3: [0, 1, 2, 3]}
Now we use the list_colouring function from vizing to find a proper
list-colouring of 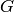 with respect to the list-assignment
with respect to the list-assignment 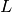 .
.
>>> from vizing.models import list_colouring
>>> list_colouring(G, L)
{0: [3], 1: [2], 2: [1], 3: [0]}
This example is just the same as ordinary proper vertex colouring. The lists didn’t impose any extra restriction. Let’s look at an example where not every colour is available at every vertex.
Forcing different colourings – complete bipartite graph¶
First we build the complete bipartite graph 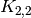 with two vertices
in each partition.
with two vertices
in each partition.
>>> G = networkx.complete_bipartite_graph(2,2)
This graph has chromatic number two. If each list has the same two colours then an ordinary vertex-colouring will give a proper list-colouring of this graph.
Instead, at each vertex we will assign the list 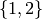 except at one
vertex which we will assign the list {2}. It’s easy to see that a proper
list-colouring is still possible under this apparently additional restriction.
except at one
vertex which we will assign the list {2}. It’s easy to see that a proper
list-colouring is still possible under this apparently additional restriction.
>>> L = {0: [2], 1:[1,2], 2:[1,2], 3:[1,2]}
>>> list_colouring(G, L)
{1: [2, 3], 2: [0, 1]}
We can use an appropriate choice of list-assignment to force certain vertices
to receive certain colours in a list-colouring. For example, if we had instead
assigned the list 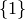 to vertex 0 we get a proper list-colouring with
colour 1 on vertex 0.
to vertex 0 we get a proper list-colouring with
colour 1 on vertex 0.
>>> L = {0: [1], 1:[1,2], 2:[1,2], 3:[1,2]}
>>> list_colouring(G, L)
{1: [0, 1], 2: [2, 3]}
This apparently trivial benefit gives us a lot of opportunity for modelling certain combinatorial problems as list-colouring instances. For example, completion problems for latin squares and Sudoku.
Constrained matrix colourings – Shidoku¶
To keep things simple, we are going to look at solving one of the small 4 x 4 Sudoku puzzles which sometimes go by the name Shidoku.

The idea here is to fill each of the empty cells (marked by a period) in such a way that every row, column and box has each of the numbers 1,2,3,4. A box here refers to the 2 x 2 regions highlighted by double borders.
It’s not too hard to see that a solution to this puzzle is the same as a proper
list-colouring of the graph  (PLUS SOME EXTRA EDGES
FOR BOX DEPENDENCIES) with list-assignment given by:
(PLUS SOME EXTRA EDGES
FOR BOX DEPENDENCIES) with list-assignment given by:
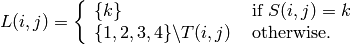
where 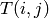 is a set containing symbols which already appear in either
the same row, column or box as cell
is a set containing symbols which already appear in either
the same row, column or box as cell 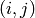 and
and 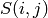 is the
symbol in row i and column j of the puzzle.
is the
symbol in row i and column j of the puzzle.
Let’s set this up as a list-colouring problem.
>>> A = { 0: [1,2,3,4,5,8,12],
1: [2,3,4,5,9,13],
2: [3,6,7,10,14],
3: [6,7,11,15],
4: [5,6,7,8,12],
5: [6,7,9,13],
6: [7,10,14],
7: [11,15],
8: [9,10,11,12,13],
9: [10,11,12,13],
10: [11,14,15],
11: [15],
12: [13,14,15],
13: [14,15],
14: [15] }
>>> G = networkx.from_dict_of_lists(A)
>>> L = { 0: [1],
1: [2],
2: [3],
3: [4],
4: [3],
5: [4],
6: [1],
7: [2],
8: [2, 4],
9: [1],
10: [4],
11: [3],
12: [3, 4],
13: [3],
14: [2],
15: [1, 4]}
>>> list_colouring(G, L)
{1: [0, 6, 9, 15], 2: [1, 7, 8, 14], 3: [2, 4, 11, 13], 4: [3, 5, 10, 12]}
Testing colourings¶
There are going to be circumstances where you want to test whether a colouring of a graph is a proper list-colouring or not. Maybe you wrote your own function to colour the graph, rather than use the models of vizing. In the module test_functions there are some useful functions for testing list-colourings.