Graph clustering_coefficient¶

clustering_coefficient(self, output_property_name=None, input_edge_labels=None)¶

Coefficient of graph with respect to labels.

Parameters:

Parameters:	output_property_name : unicode (default=None) The name of the new property to which each vertex’s local clustering coefficient will be written. If this option is not specified, no output frame will be produced and only the global clustering coefficient will be returned. input_edge_labels : list (default=None) If this list is provided, only edges whose labels are included in the given set will be considered in the clustering coefficient calculation. In the default situation (when no list is provided), all edges will be used in the calculation, regardless of label. It is required that all edges that enter into the clustering coefficient analysis be undirected.
Returns:	: dict Dictionary of the global clustering coefficient of the graph or, if local clustering coefficients are requested, a reference to the frame with local clustering coefficients stored at properties at each vertex.

output_property_name : unicode (default=None)

The name of the new property to which each vertex’s local clustering coefficient will be written. If this option is not specified, no output frame will be produced and only the global clustering coefficient will be returned.

input_edge_labels : list (default=None)

If this list is provided, only edges whose labels are included in the given set will be considered in the clustering coefficient calculation. In the default situation (when no list is provided), all edges will be used in the calculation, regardless of label. It is required that all edges that enter into the clustering coefficient analysis be undirected.

Returns:

: dict

Dictionary of the global clustering coefficient of the graph or, if local clustering coefficients are requested, a reference to the frame with local clustering coefficients stored at properties at each vertex.

Calculates the clustering coefficient of the graph with respect to an (optional) set of labels.

Pulls graph from underlying store, calculates degrees and writes them into the property specified, and then writes the output graph to the underlying store.

Warning

THIS FUNCTION IS FOR UNDIRECTED GRAPHS. If it is called on a directed graph, its output is NOT guaranteed to calculate the local directed clustering coefficients.

Clustering Coefficients

The clustering coefficient of a graph provides a measure of how tightly clustered an undirected graph is. Informally, if the edge relation denotes “friendship”, the clustering coefficient of the graph is the probability that two people are friends given that they share a common friend.

More formally:

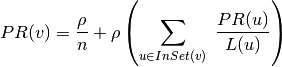
$cc(G) = \frac{ \| \{ (u,v,w) \in V^3: \ \{u,v\}, \{u, w\}, \{v,w \} \in \ E \} \| }{\| \{ (u,v,w) \in V^3: \ \{u,v\}, \{u, w\} \in E \} \|}$

Analogously, the clustering coefficient of a vertex provides a measure of how tightly clustered that vertex’s neighborhood is. Informally, if the edge relation denotes “friendship”, the clustering coefficient at a vertex $v$ is the probability that two acquaintances of $v$ are themselves friends.

More formally:

$cc(v) = \frac{ \| \{ (u,v,w) \in V^3: \ \{u,v\}, \{u, w\}, \{v,w \} \in \ E \} \| }{\| \{ (u,v,w) \in V^3: \ \{v, u \}, \{v, w\} \in E \} \|}$

The toolkit provides the function clustering_coefficient which computes both local and global clustering coefficients for a given undirected graph.

For more details on the mathematics and applications of clustering coefficients, see http://en.wikipedia.org/wiki/Clustering_coefficient.

Examples

>>> graph = ta.Graph()

>>> graph.define_vertex_type('source')
[===Job Progress===]
>>> graph.vertices['source'].add_vertices(vertex_frame, 'source', 'label')
[===Job Progress===]
>>> graph.define_edge_type('edges','source', 'source', directed=False)
[===Job Progress===]
>>> graph.edges['edges'].add_edges(edge_frame, 'source', 'dest', ['weight'])
[===Job Progress===]
>>> results = graph.clustering_coefficient('ccgraph')
[===Job Progress===]
>>> results.global_clustering_coefficient
0.5
>>> results.frame.inspect()
[#]  _label  source  label  ccgraph
==========================================
[0]  source       5    5.0             0.0
[1]  source       1    1.0  0.333333333333
[2]  source       2    1.0             1.0
[3]  source       3    5.0             1.0
[4]  source       4    5.0             0.0

Quick search

Table Of Contents

Graph clustering_coefficient¶