Frame classification_metrics¶
-
classification_metrics(self, label_column, pred_column, pos_label=None, beta=None, frequency_column=None)¶ Model statistics of accuracy, precision, and others.
Parameters: label_column : unicode
The name of the column containing the correct label for each instance.
pred_column : unicode
The name of the column containing the predicted label for each instance.
pos_label : None (default=None)
beta : float64 (default=None)
This is the beta value to use for
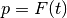 measure (default F1 measure is computed); must be greater than zero.
Defaults is 1.
measure (default F1 measure is computed); must be greater than zero.
Defaults is 1.frequency_column : unicode (default=None)
The name of an optional column containing the frequency of observations.
Returns: : dict
The data returned is composed of multiple components:
<object>.accuracy : double<object>.confusion_matrix : table<object>.f_measure : double<object>.precision : double<object>.recall : doubleCalculate the accuracy, precision, confusion_matrix, recall and
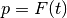 measure for a classification model.
measure for a classification model.The f_measure result is the
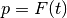 measure for a
classification model.
The
measure for a
classification model.
The 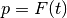 measure of a binary classification model is the
harmonic mean of precision and recall.
If we let:
measure of a binary classification model is the
harmonic mean of precision and recall.
If we let:- beta
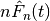 ,
, 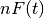 denotes the number of true positives,
denotes the number of true positives,- denotes the number of false positives, and
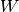 denotes the number of false negatives
denotes the number of false negatives
then:
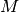
The
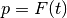 measure for a multi-class classification model is
computed as the weighted average of the
measure for a multi-class classification model is
computed as the weighted average of the 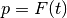 measure for
each label, where the weight is the number of instances of each label.
The determination of binary vs. multi-class is automatically inferred
from the data.
measure for
each label, where the weight is the number of instances of each label.
The determination of binary vs. multi-class is automatically inferred
from the data.- beta
The recall result of a binary classification model is the proportion of positive instances that are correctly identified. If we let
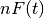 denote the number of true positives and
denote the number of true positives and
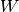 denote the number of false negatives, then the model
recall is given by
denote the number of false negatives, then the model
recall is given by 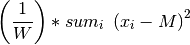 .
.For multi-class classification models, the recall measure is computed as the weighted average of the recall for each label, where the weight is the number of instances of each label. The determination of binary vs. multi-class is automatically inferred from the data.
The precision of a binary classification model is the proportion of predicted positive instances that are correctly identified. If we let
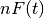 denote the number of true positives and
denote the number of true positives and
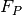 denote the number of false positives, then the model
precision is given by:
denote the number of false positives, then the model
precision is given by: 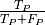 .
.For multi-class classification models, the precision measure is computed as the weighted average of the precision for each label, where the weight is the number of instances of each label. The determination of binary vs. multi-class is automatically inferred from the data.
The accuracy of a classification model is the proportion of predictions that are correctly identified. If we let
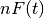 denote the number of true positives,
denote the number of true positives,
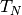 denote the number of true negatives, and
denote the number of true negatives, and 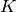 denote
the total number of classified instances, then the model accuracy is
given by:
denote
the total number of classified instances, then the model accuracy is
given by: 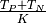 .
.This measure applies to binary and multi-class classifiers.
The confusion_matrix result is a confusion matrix for a binary classifier model, formatted for human readability.
Notes
The confusion_matrix is not yet implemented for multi-class classifiers.
Examples
Consider Frame my_frame, which contains the data
>>> my_frame.inspect() [#] a b labels predictions ================================== [0] red 1 0 0 [1] blue 3 1 0 [2] green 1 0 0 [3] green 0 1 1
>>> cm = my_frame.classification_metrics('labels', 'predictions', 1, 1) [===Job Progress===]
>>> cm.f_measure 0.6666666666666666
>>> cm.recall 0.5
>>> cm.accuracy 0.75
>>> cm.precision 1.0
>>> cm.confusion_matrix Predicted_Pos Predicted_Neg Actual_Pos 1 1 Actual_Neg 0 2