The geodrawing controller

We are going to demonstrate the controller class that maintains a map background for cairo surfaces with an added geo coordinate system:

from tl.geodrawing.controller import GeoSurfaceController

Coordinate systems

A geo-surface controller exposes two coordinate systems:

• geo coordinates (longitudes and latitudes expressed in degrees)
• integer pixel numbers relative to an image surface called the viewport that represents a portion of the map, with the origin at the top left

The controller methods px2geo and geo2px transform pixels into geo coordinates and vice versa. The transformation depends on the controller’s state described by width and height, zoom level and center geo-coordinates.

The default viewport: a whole-world surface

Let’s first have a look at the smallest possible whole-world surface:

c = GeoSurfaceController()
c.width = 256
c.height = 256
c.zoom = 0
c.center = (0, 0)

>>> c.px2geo(0, 0)
(-179.29687..., 84.99010...)
>>> c.px2geo(255, 255)
(179.29687..., -84.99010...)
>>> c.px2geo(127, 127)
(-0.70312..., 0.70310...)
>>> c.px2geo(128, 128)
(0.70312..., -0.70310...)

>>> c.geo2px(179.5, 85.0)
(255, 0)
>>> c.geo2px(-179.5, -85.0)
(0, 255)
>>> c.geo2px(0, 0)
(128, 128)
>>> c.geo2px(-0.5, 0.5)
(127, 127)
>>> c.geo2px(0.5, -0.5)
(128, 128)

As it would be a little awkward having to transform geo-coordinates to pixels explicitly before each drawing operation, a geo-coordinate controller is able to apply coordinate transformations to cairo contexts. The surface of a context thus transformed is addressed by a coordinate pair of longitude and Mercator-transformed latitude. Let’s first create a surface and draw a frame displaying the border coordinates around it [1]:

from tl.geodrawing.controller import mercator
import cairo

surface = cairo.ImageSurface(cairo.FORMAT_ARGB32, 256, 256)
ctx = cairo.Context(surface)
c.draw_frame(ctx)

Now we transform the context’s coordinate system; the transformation matrix will then translate the origin to the surface’s center and map the geo-coordinate range from -180 degrees to 180 degrees horizontally by -1 to 1 vertically to pixel coordinates ranging from -128 to 128 both ways:

>>> c.transform_for_geo(ctx)
>>> ctx.get_matrix()
cairo.Matrix(0.711111, 0, 0, -128, 128, 128)

Let’s draw something simple to the surface using geo coordinates now:

ctx.move_to(-90, mercator(-45))
ctx.line_to(-90, mercator(60))
ctx.line_to(135, mercator(-60))
ctx.identity_matrix()
ctx.stroke()

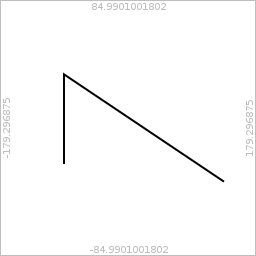
surface # options: exclude=exclude_coordinates

The geo-coordinate transformation can be applied to a cairo drawing context using a Python context manager that restores the cairo context’s transformation matrix when it exits. To see this more clearly, we operate on a context that is scaled at the outset:

from tl.geodrawing.controller import mercator
import cairo

surface = cairo.ImageSurface(cairo.FORMAT_ARGB32, 256, 256)
ctx = cairo.Context(surface)
ctx.scale(1, 5)
c.draw_frame(ctx)

We apply the geo-transformation context manager now in order to draw something to the surface using geo coordinates. At that point, the context’s transformation matrix is independent of any previous transformations:

>>> with c.transformed_for_geo(ctx):
...     ctx.move_to(-90, mercator(-45))
...     ctx.line_to(-90, mercator(60))
...     ctx.line_to(135, mercator(-60))
...     ctx.get_matrix()
cairo.Matrix(0.711111, 0, 0, -128, 128, 128)

After the context manager has exited, the context’s transformation matrix is back to its old value and applies to the stroke:

>>> ctx.get_matrix()
cairo.Matrix(1, 0, 0, 5, 0, 0)
>>> ctx.stroke()

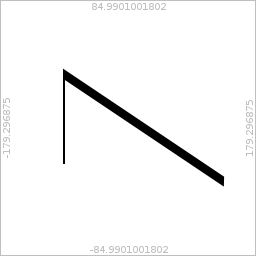
surface # options: exclude=exclude_coordinates

Changing the viewport

Now we use a different zoom level:

c.width = 4096
c.height = 4096
c.zoom = 4

ctx.identity_matrix()

>>> c.px2geo(0, 0)
(-179.95605..., 85.04733...)
>>> c.px2geo(2048, 2048)
(0.04394..., -0.04394...)

>>> c.geo2px(-179.5, 85.0)
(5, 6)
>>> c.geo2px(0, 0)
(2048, 2048)
>>> c.geo2px(0.5, 0.5)
(2053, 2042)

>>> c.transform_for_geo(ctx)
>>> ctx.get_matrix()
cairo.Matrix(11.3778, 0, 0, -2048, 2048, 2048)

Finally, we zoom in even further and restrict our viewport to a portion of the map centered at the middle of the upper right quarter of the world map:

c.width = 300
c.height = 200
c.zoom = 6
c.center = (90, 45)

surface = cairo.ImageSurface(cairo.FORMAT_ARGB32, 300, 200)
ctx = cairo.Context(surface)
c.draw_frame(ctx)

>>> c.px2geo(0, 0)
(86.71508..., 46.52508...)
>>> c.px2geo(150, 99)
(90.01098..., 45.00776...)
>>> c.px2geo(149, 100)
(89.98901..., 44.99223...)
>>> c.px2geo(299, 199)
(93.28491..., 43.43321...)

>>> c.geo2px(86.715, 46.525)
(0, 0)
>>> c.geo2px(89.99, 45.01)
(149, 99)
>>> c.geo2px(90, 45)
(150, 100)
>>> c.geo2px(93.285, 43.433)
(299, 199)

>>> with c.transformed_for_geo(ctx):
...     ctx.move_to(88, mercator(44))
...     ctx.line_to(92, mercator(45))
...     ctx.line_to(90, mercator(46))
...     ctx.get_matrix()
cairo.Matrix(45.5111, 0, 0, -8192, -3946, 2398.26)

>>> ctx.get_matrix()
cairo.Matrix(1, 0, 0, 1, 0, 0)
>>> ctx.stroke()

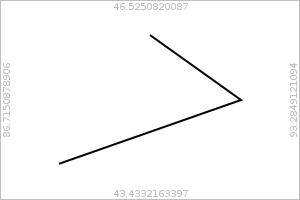
surface # options: exclude=exclude_coordinates_2

The map surface

Besides performing state-dependent geo-coordinate transformations, a geo-surface controller maintains a cairo surface that shows a part of a map of the world, depending on the controller’s state and meant to be copied as a drawing background to other cairo surfaces. For imagery, map tiles sized 256 by 256 pixels are obtained from a tile source. Tile sources might pull the images from services such as OpenStreetMap.

Keeping the surface up-to-date with the viewport

We create a geo-surface controller using a testing tile source:

import tl.geodrawing.tests
c = GeoSurfaceController(
     tile_source=tl.geodrawing.tests.TileSource(name='testing'))

c.width = 300
c.height = 300

In the default state, the surface’s background shows a map of the whole world:

>>> c.update_surface()
>>> c.surface
<cairo.ImageSurface object at 0x...>

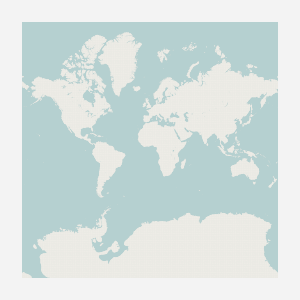
c.surface

When the viewport changes, the controller’s maintained surface isn’t updated immediately. Surface updates must be requested by the application to avoid unnecessary intermediate updates, for example when the viewport is being changed in complex ways. At each update, the old surface content is reused before the controller tries to copy fresh tiles to the surface. This gives the user immediate feed-back before new tiles have been obtained. To make this possible, the controller maintains a coordinate transformation that represents the combined transformations since the last surface update.

The transformation is the identity right after each surface update:

>>> c.transform
cairo.Matrix(1, 0, 0, 1, 0, 0)

After zooming into the map, we see that the transformation has been updated automatically. It describes a combination of scaling up by 2 zoom levels and re-centering the surface:

>>> c.zoom = 2
>>> c.transform
cairo.Matrix(4, 0, 0, 4, -450, -450)

When we update the surface, the transformation is applied to scale and re-center the previous surface content, then reset:

>>> c.update_surface()
>>> c.transform
cairo.Matrix(1, 0, 0, 1, 0, 0)

Since our tile source provides only one of the tiles needed to cover the new viewport, the scaled old surface remains visible in three quarters of the image:

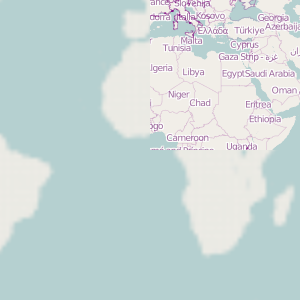
c.surface

The tile source usually implies a maximum zoom value it provides tiles for; it’s 5 for our testing tile source. We can read this value from the controller:

>>> c.max_zoom
5

However, this does not mean we cannot zoom beyond this value, provided we know what we are doing:

>>> c.zoom = 10
>>> c.transform
cairo.Matrix(256, 0, 0, 256, -38250, -38250)

Next, let’s watch how changing the viewport more than once in a row leaves its trail on the combined transformation:

>>> c.zoom = 2
>>> c.transform
cairo.Matrix(1, 0, 0, 1, 0, 0)
>>> c.width = 400
>>> c.transform
cairo.Matrix(1, 0, 0, 1, 50, 0)
>>> c.height= 240
>>> c.transform
cairo.Matrix(1, 0, 0, 1, 50, -30)
>>> c.center = (10, 15)
>>> c.transform
cairo.Matrix(1, 0, 0, 1, 21.5556, 13.1626)

These last transformations made the viewport wider than it had been and moved it to include some area north of what was covered by the previous image. Since those parts of the whole-world map that were moved outside the bounds of the surface by the first scaling had been lost when we updated the surface to create the previously shown image, the surface will have blank margins at the sides and top after the next update:

>>> c.update_surface()

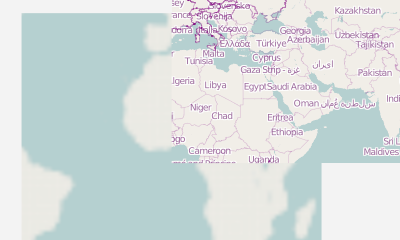
c.surface

On the other hand, scaling the surface up by 8 more zoom levels and back down again did not cut away from the sides of that earlier image. This is an effect of the transformation being accumulated between surface updates: changing the viewport is not destructive in itself. Maintaining the transformation is thus an optimisation not only for performance, but also for maximal reuse of the old surface content.

Some convenience transformations of the viewport

In addition to geo-coordinates, the viewport’s center can be addressed in terms of pixels. This takes a lot of arithmetics out of application code that, for example, allows dragging a geo-controlled drawing area around using the mouse. The absolute pixel values refer to an imaginary surface that covers the whole map at the current zoom level, with the origin at the lower left:

>>> c.zoom = 3 # whole map: 2048 by 2048 pixels
>>> c.center = (135, 45)
>>> c.transform
cairo.Matrix(2, 0, 0, 2, -911.111, 80.958)
>>> c.center_xy
(1792.0, 1311.28312...)

Setting the pixel values of the center updates both its geo-coordinates and the current transformation:

>>> c.center_xy = (1536, 1200)
>>> c.center
(90.0, 29.53522...)
>>> c.transform
cairo.Matrix(2, 0, 0, 2, -655.111, -30.3252)

Moving the viewport by a given amount of pixels is made even more convenient by a method of the controller, which takes as arguments the pixel numbers by which to move the map right and up inside the viewport, thereby moving the center of the viewport left and down across the map by the same distances:

>>> c.move_rel(256, 100)
>>> c.center_xy
(1280, 1100)
>>> c.center
(45.0, 13.23994...)
>>> c.transform
cairo.Matrix(2, 0, 0, 2, -399.111, -130.325)

Another convenience function allows scaling the map up or down by a given number of zoom levels while keeping the location displayed at a given pixel fixed. Let’s zoom into the map by two levels around a point in the lower left of the viewport:

>>> c.width = 300
>>> c.height = 200
>>> c.zoom_rel(50, 150, 2)
>>> c.zoom
5
>>> c.center_xy
(4820.0, 4250.0)
>>> c.center
(31.81640625, 6.75189...)
>>> c.transform
cairo.Matrix(8, 0, 0, 8, -1946.44, -1051.3)

Furthermore, we can freely specify a piece of the map that should be fit inside the viewport by giving the geo-coordinates of its bottom left and top right corners:

>>> c.view(30, 40, 50, 60)
>>> c.zoom
3
>>> c.center_xy
(1251.55555..., 1362.96571...)
>>> c.center
(40.0, 51.06522...)
>>> c.transform
cairo.Matrix(2, 0, 0, 2, -420.667, 112.641)

We can have a fraction of the viewport inside its edges considered padding so that the piece of map is fit inside only part of the viewport, but centered at the same geo-coordinates:

>>> c.view(30, 40, 50, 60, padding=0.2)
>>> c.zoom
2
>>> c.center_xy
(625.77777..., 681.48285...)
>>> c.center
(40.0, 51.06522...)
>>> c.transform
cairo.Matrix(1, 0, 0, 1, -135.333, 106.32)

Finally, we can have the viewport centered around a geo-coordinate point without specifying the size of the area shown around it simply by using a zero-size piece of map. An area of 1/200 degrees squared will be fit inside the viewport in that case:

>>> c.view(30, 40, 30, 40)
>>> c.zoom
7
>>> c.center_xy
(19114.66666..., 20362.71815...)
>>> c.center
(30.0, 40.0)
>>> c.transform
cairo.Matrix(32, 0, 0, 32, -8070.44, -1142.48)

Footnotes

[1]	Make tests ignore text in an unpredictable font >>> exclude_coordinates = [(91, 2, 76, 9), (2, 97, 9, 62), ... (89, 245, 80, 9), (245, 99, 9, 58)] >>> exclude_coordinates_2 = [(113, 2, 76, 9), (2, 62, 9, 76), ... (113, 189, 76, 9), (289, 62, 9, 76)]