Fitting Types¶
Fit (Least Squares)¶
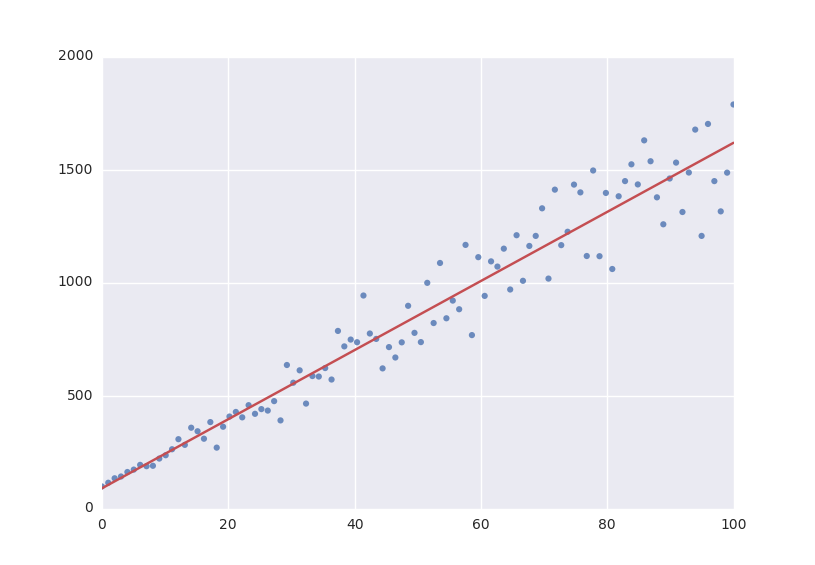
The default fitting object does least-squares fitting:
from symfit import parameters, variables, Fit
import numpy as np
# Define a model to fit to.
a, b = parameters('a, b')
x = variables('x')
model = a * x + b
# Generate some data
xdata = np.linspace(0, 100, 100) # From 0 to 100 in 100 steps
a_vec = np.random.normal(15.0, scale=2.0, size=(100,))
b_vec = np.random.normal(100.0, scale=2.0, size=(100,))
# Point scattered around the line 5 * x + 105
ydata = a_vec * xdata + b_vec
fit = Fit(model, xdata, ydata)
fit_result = fit.execute()
The Fit object also supports standard deviations. In
order to provide these, it’s nicer to use a named model:
a, b = parameters('a, b')
x, y = variables('x, y')
model = {y: a * x + b}
fit = Fit(model, x=xdata, y=ydata, sigma_y=sigma)
Warning
symfit assumes these sigma to be from measurement errors by
default, and not just as a relative weight. This means the standard
deviations on parameters are calculated assuming the absolute size of sigma
is significant. This is the case for measurement errors and therefore for
most use cases symfit was designed for. If you only want to use the
sigma for relative weights, then you can use absolute_sigma=False as a
keyword argument.
Please note that this is the opposite of the convention used by scipy’s
curve_fit(). Looking through their mailing list this
seems to have been implemented the ‘wrong’ way for historical reasons, and
was understandably never changed so as not to loose backwards compatibility.
Since this is a new project, we don’t have that problem.
Constrained Least Squares Fit¶
The Fit takes a constraints keyword; a list of
relationships between the parameters that has to be respected. As an example of
fitting with constraints, we could imagine fitting the angles of a triangle:
a, b, c = parameters('a, b, c')
a_i, b_i, c_i = variables('a_i, b_i, c_i')
model = {a_i: a, b_i: b, c_i: c}
data = np.array([
[10.1, 9., 10.5, 11.2, 9.5, 9.6, 10.],
[102.1, 101., 100.4, 100.8, 99.2, 100., 100.8],
[71.6, 73.2, 69.5, 70.2, 70.8, 70.6, 70.1],
])
fit = Fit(
model=model,
a_i=data[0],
b_i=data[1],
c_i=data[2],
constraints=[Equality(a + b + c, 180)]
)
fit_result = fit.execute()
The line constraints=[Equality(a + b + c, 180)] ensures the our basic
knowledge of geometry is respected despite my sloppy measurements.
Note
Under the hood, ConstrainedNumericalLeastSquares
is used to perform the fit. Fit tries to select the
right fitting object based on the problem you present it with.
See Fit for more.
(Non)LinearLeastSquares¶
The LinearLeastSquares implements the analytical
solution to Least Squares fitting. When your model is linear in it’s parameters,
consider using this rather than the default
NumericalLeastSquares since this gives the exact
solution in one step, no iteration and no guesses needed.
NonLinearLeastSquares is the generalization to
non-linear models. It works by approximating the model by a linear one around
the value of your guesses and repeating that process iteratively. This process
is therefore very sensitive to getting good initial guesses.
Notes on these objects:
- Use
NonLinearLeastSquaresinstead ofLinearLeastSquaresunless you have a reason not to.NonLinearLeastSquareswill behave exactly the same asLinearLeastSquareswhen the model is linear. - Bounds are currently ignored by both. This is because for linear models there can only be one solution. For non-linear models it simply hasn’t been considered yet.
- When performance matters, use
NumericalLeastSquaresinstead ofNonLinearLeastSquares. These analytical objects are implemented in pure python and are therefore massively outgunned byNumericalLeastSquareswhich is ultimately a wrapper to MINPACK.
Likelihood¶
Given a dataset and a model, what values should the model’s parameters have to make the observed data most likely? This is the principle of maximum likelihood and the question the Likelihood object can answer for you.
Example:
from symfit import Parameter, Variable, Likelihood, exp
import numpy as np
# Define the model for an exponential distribution (numpy style)
beta = Parameter()
x = Variable()
model = (1 / beta) * exp(-x / beta)
# Draw 100 samples from an exponential distribution with beta=5.5
data = np.random.exponential(5.5, 100)
# Do the fitting!
fit = Likelihood(model, data)
fit_result = fit.execute()
Off-course fit_result is a normal FitResults
object. Because scipy.optimize.minimize() is used to do the actual work,
bounds on parameters, and even constraints are supported. For more information
on this subject, check out symfit‘s Minimize.
Minimize/Maximize¶
Minimize or Maximize a model subject to bounds and/or constraints. It is a
wrapper to scipy.optimize.minimize(). As an example I present an example
from the scipy docs.
Suppose we want to maximize the following function:
Subject to the following constraints:
In SciPy code the following lines are needed:
def func(x, sign=1.0):
""" Objective function """
return sign*(2*x[0]*x[1] + 2*x[0] - x[0]**2 - 2*x[1]**2)
def func_deriv(x, sign=1.0):
""" Derivative of objective function """
dfdx0 = sign*(-2*x[0] + 2*x[1] + 2)
dfdx1 = sign*(2*x[0] - 4*x[1])
return np.array([ dfdx0, dfdx1 ])
cons = ({'type': 'eq',
'fun' : lambda x: np.array([x[0]**3 - x[1]]),
'jac' : lambda x: np.array([3.0*(x[0]**2.0), -1.0])},
{'type': 'ineq',
'fun' : lambda x: np.array([x[1] - 1]),
'jac' : lambda x: np.array([0.0, 1.0])})
res = minimize(func, [-1.0,1.0], args=(-1.0,), jac=func_deriv,
constraints=cons, method='SLSQP', options={'disp': True})
Takes a couple of read-throughs to make sense, doesn’t it? Let’s do the same
problem in symfit:
from symfit import parameters, Maximize, Eq, Ge
x, y = parameters('x, y')
model = 2*x*y + 2*x - x**2 -2*y**2
constraints = [
Eq(x**3 - y, 0),
Ge(y - 1, 0),
]
fit = Maximize(model, constraints=constraints)
fit_result = fit.execute()
Done! symfit will determine all derivatives automatically, no need for
you to think about it.
Warning
You might have noticed that x and y are
Parameter‘s in the above problem, which may
strike you as weird. However, it makes perfect sense because in this problem
they are parameters to be optimised, not independent variables. Furthermore,
this way of defining it is consistent with the treatment of
Variable‘s and
Parameter‘s in symfit. Be aware of this
when using Minimize, as the whole process won’t
work otherwise.
ODE Fitting¶
Fitting to a system of ordinary differential equations (ODEs) is also
remarkedly simple with symfit. Let’s do a simple example from reaction
kinetics. Suppose we have a reaction A + A -> B with rate constant \(k\).
We then need the following system of rate equations:
In symfit, this becomes:
model_dict = {
D(a, t): - k * a**2,
D(b, t): k * a**2,
}
We see that the symfit code is already very readable. Let’s do a fit to
this:
tdata = np.array([10, 26, 44, 70, 120])
adata = 10e-4 * np.array([44, 34, 27, 20, 14])
a, b, t = variables('a, b, t')
k = Parameter(0.1)
a0 = 54 * 10e-4
model_dict = {
D(a, t): - k * a**2,
D(b, t): k * a**2,
}
ode_model = ODEModel(model_dict, initial={t: 0.0, a: a0, b: 0.0})
fit = Fit(ode_model, t=tdata, a=adata, b=None)
fit_result = fit.execute()
That’s it! An ODEModel behaves just like any other
model object, so Fit knows how to deal with it! Note
that since we don’t know the concentration of B, we explicitly set b=None
when calling Fit so it will be ignored.
Warning
Fitting to ODEs is extremely difficult from an algorithmic point of view, since these systems are usually very sensitive to the parameters. Using (very) good initial guesses for the parameters and initial values is critical!
Upon every iteration of performing the fit the ODEModel is integrated again from the initial point using the new guesses for the parameters.
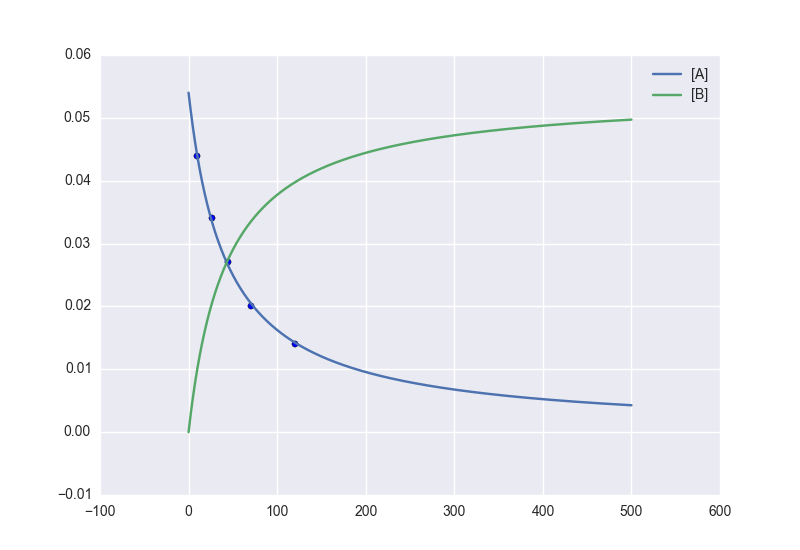
We can plot it just like always:
# Generate some data
tvec = np.linspace(0, 500, 1000)
A, B = ode_model(t=tvec, **fit_result.params)
plt.plot(tvec, A, label='[A]')
plt.plot(tvec, B, label='[B]')
plt.scatter(tdata, adata)
plt.legend()
plt.show()
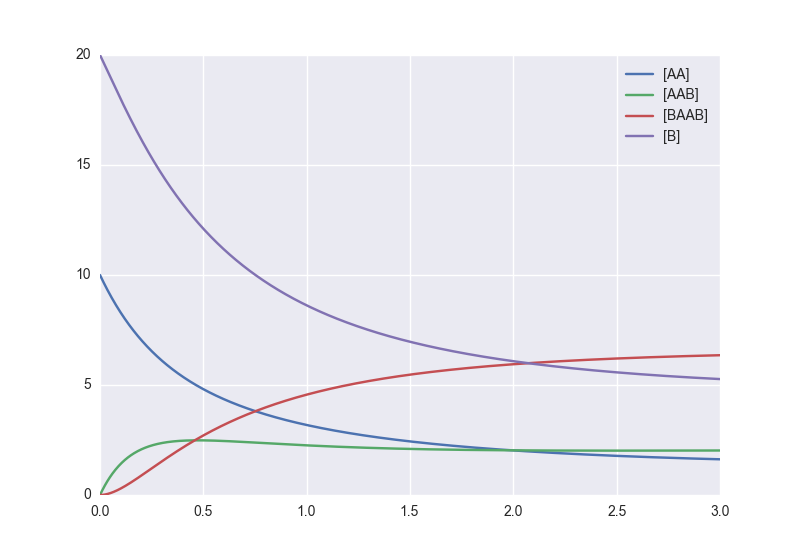
As an example of the power of symfit‘s ODE syntax, let’s have a look at
a system with 2 equilibria: compound AA + B <-> AAB and AAB + B <-> d.
In symfit these can be implemented as:
AA, B, AAB, BAAB, t = variables('AA, B, AAB, BAAB, t')
k, p, l, m = parameters('k, p, l, m')
AA_0 = 10 # Some made up initial amound of [AA]
B = AA_0 - BAAB + AA # [B] is not independent.
model_dict = {
D(BAAB, t): l * AAB * B - m * BAAB,
D(AAB, t): k * A * B - p * AAB - l * AAB * B + m * BAAB,
D(A, t): - k * A * B + p * AAB,
}
The result is as readable as one can reasonably expect from a multicomponent system (and while using chemical notation). Let’s plot the model for some kinetics constants:
model = ODEModel(model_dict, initial={t: 0.0, AA: AA_0, AAB: 0.0, BAAB: 0.0})
# Generate some data
tdata = np.linspace(0, 3, 1000)
# Eval the normal way.
AA, AAB, BAAB = model(t=tdata, k=0.1, l=0.2, m=0.3, p=0.3)
plt.plot(tdata, AA, color='red', label='[AA]')
plt.plot(tdata, AAB, color='blue', label='[AAB]')
plt.plot(tdata, BAAB, color='green', label='[BAAB]')
plt.plot(tdata, B(BAAB=BAAB, AA=AA), color='pink', label='[B]')
# plt.plot(tdata, AA + AAB + BAAB, color='black', label='total')
plt.legend()
plt.show()
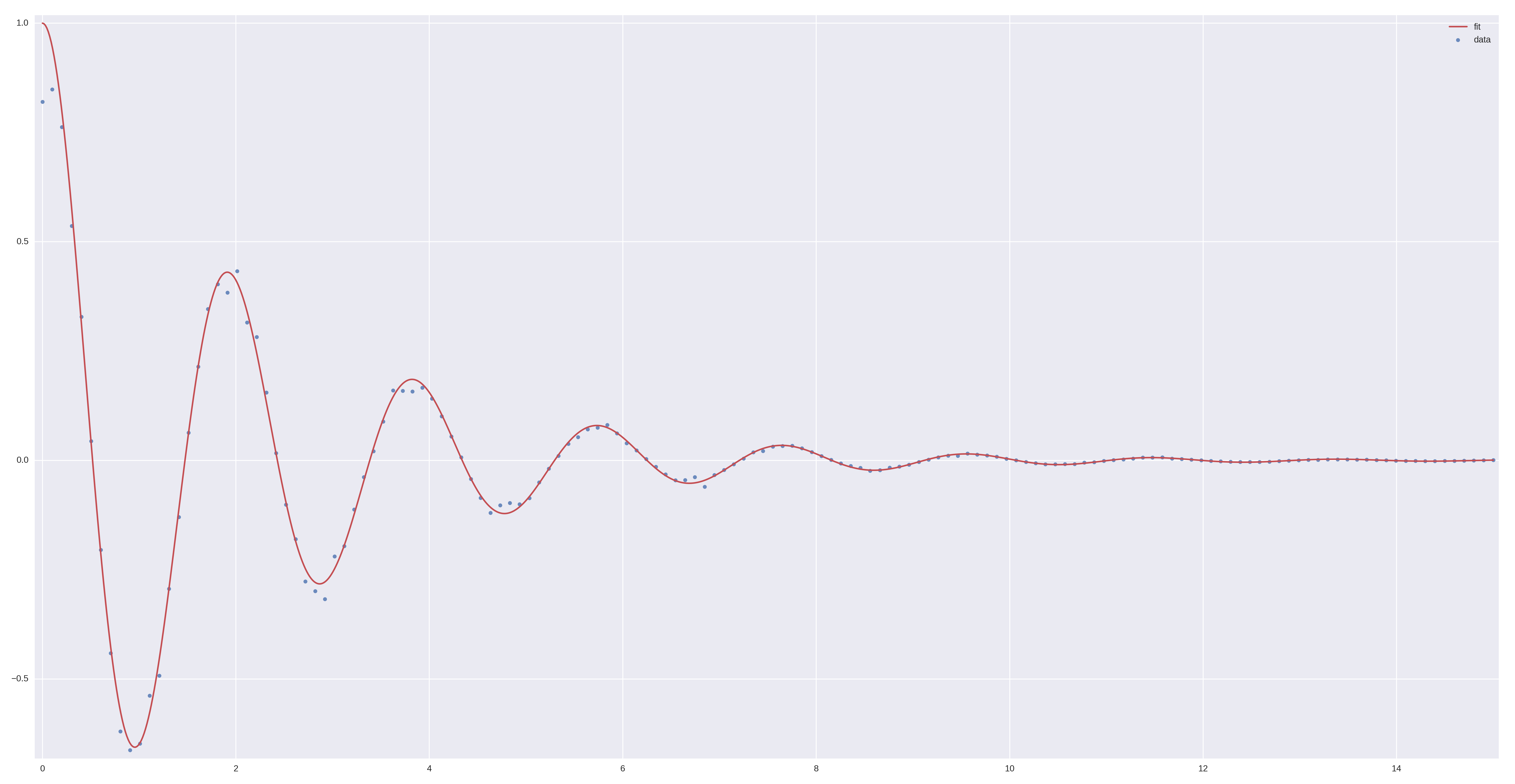
More common examples, such as dampened harmonic oscillators also work as expected:
# Oscillator strength
k = Parameter()
# Mass, just there for the physics
m = 1
# Dampening factor
gamma = Parameter()
x, v, t = symfit.variables('x, v, t')
# Define the force based on Hooke's law, and dampening
a = (-k * x - gamma * v)/m
model_dict = {
D(x, t): v,
D(v, t): a,
}
ode_model = ODEModel(model_dict, initial={t: 0, v: 0, x: 1})
# Let's create some data...
times = np.linspace(0, 15, 150)
data = ode_model(times, k=11, gamma=0.9, m=m.value).x
# ... and add some noise to it.
noise = np.random.normal(1, 0.1, data.shape) # 10% error
data *= noise
fit = Fit(ode_model, t=times, x=data)
fit_result = fit.execute()
Note
Evaluating the model above will produce a named tuple with values for
both x and v. Since we are only interested in the values for x,
we immediately select it with .x.
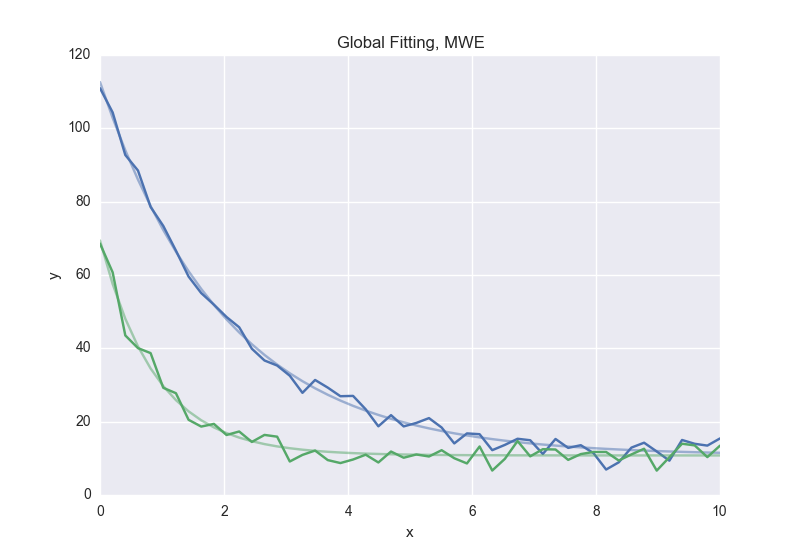
Global Fitting¶
In a global fitting problem, we fit to multiple datasets where one or more
parameters might be shared. The same syntax used for ODE fitting makes this
problem very easy to solve in symfit.
As a simple example, suppose we have two datasets measuring exponential decay, with the same background, but different amplitude and decay rate.
In order to fit to this, we define the following model:
x_1, x_2, y_1, y_2 = variables('x_1, x_2, y_1, y_2')
y0, a_1, a_2, b_1, b_2 = parameters('y0, a_1, a_2, b_1, b_2')
model = Model({
y_1: y0 + a_1 * exp(- b_1 * x_1),
y_2: y0 + a_2 * exp(- b_2 * x_2),
})
Note that y0 is shared between the components. Fitting is then done in the
normal way:
fit = Fit(model, x_1=xdata1, x_2=xdata2, y_1=ydata1, y_2=ydata2)
fit_result = fit.execute()
Warning
The regression coefficient is not properly defined for vector-valued models, but it is still listed! Until this is fixed, please recalculate it on your own for every component using the bestfit parameters.
Do not cite the overall \(R^2\) given by symfit.
Advanced usage¶
In general, the separate components of the model can be whatever you need them to be. You can mix and match which variables and parameters should be coupled and decoupled ad lib. Some examples are given below.
Same parameters and same function, different (in)dependent variables:
datasets = [data_1, data_2, data_3, data_4, data_5, data_6]
xs = variables('x_1, x_2, x_3, x_4, x_5, x_6')
ys = variables('y_1, y_2, y_3, y_4, y_5, y_6')
zs = variables(', '.join('z_{}'.format(i) for i in range(1, 7)))
a, b = parameters('a, b')
model_dict = {
z: a/(y * b) * exp(- a * x)
for x, y, z in zip(xs, ys, zs)
}
What if the model is unnamed?¶
Then you’ll have to use the ordering. Variables throughout symfit‘s
objects are internally ordered in the following way: first independent
variables, then dependent variables, then sigma variables, and lastly
parameters when applicable. Within each group alphabetical ordering applies.
It is therefore always possible to assign data to variables in an unambiguous way using this ordering. For example:
fit = Fit(model, x_data, y_data, sigma_y_data)