geostrophic¶
-
seawater.geostrophic.bfrq(s, t, p, lat=None)¶ Calculates Brünt-Väisälä Frequency squared (N 2) at the mid depths from the equation:
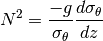
Also calculates Potential Vorticity from:
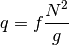
Parameters: s(p) : array_like
salinity [psu (PSS-78)]
t(p) : array_like
temperature or potential temperature [℃ (ITS-90)]
p : array_like
pressure [db].
lat : number or array_like, optional
latitude in decimal degrees north [-90..+90]. Will grav instead of the default g = 9.8 m 2 s -1) and d(z) instead of d(p)
Returns: n2 : array_like
Brünt-Väisälä Frequency squared (M-1xN) [rad s -2]
q : array_like
planetary potential vorticity (M-1xN) [ m s -1]
p_ave : array_like
mid pressure between P grid (M-1xN) [db]
References
[R30] A.E. Gill 1982. p.54 Eqn. 3.7.15 “Atmosphere-Ocean Dynamics” Academic Press: New York. ISBN: 0-12-283522-0 [R31] Jackett, David R., Trevor J. Mcdougall, 1995: Minimal Adjustment of Hydrographic Profiles to Achieve Static Stability. J. Atmos. Oceanic Technol., 12, 381-389. doi: 10.1175/1520-0426(1995)012<0381:MAOHPT>2.0.CO;2 Examples
>>> import seawater as sw >>> s = [[0, 0, 0], [15, 15, 15], [30, 30, 30],[35,35,35]] >>> t = [[15]*3]*4 >>> p = [[0], [250], [500], [1000]] >>> lat = [30,32,35] >>> sw.bfrq(s, t, p, lat)[0] array([[ 4.51543648e-04, 4.51690708e-04, 4.51920753e-04], [ 4.45598092e-04, 4.45743207e-04, 4.45970207e-04], [ 7.40996788e-05, 7.41238078e-05, 7.41615525e-05]])
-
seawater.geostrophic.svan(s, t, p=0)¶ Specific Volume Anomaly calculated as svan = 1 / dens(s, t, p) - 1 / dens(35, 0, p).
Note that it is often quoted in literature as 1e8 * units.
Parameters: s(p) : array_like
salinity [psu (PSS-78)]
t(p) : array_like
temperature [℃ (ITS-90)]
p : array_like
pressure [db].
Returns: svan : array_like
specific volume anomaly [m 3 kg -1]
References
[R32] Fofonoff, P. and Millard, R.C. Jr UNESCO 1983. Algorithms for computation of fundamental properties of seawater. UNESCO Tech. Pap. in Mar. Sci., No. 44, 53 pp. Eqn.(31) p.39. http://unesdoc.unesco.org/images/0005/000598/059832eb.pdf [R33] S. Pond & G.Pickard 2nd Edition 1986 Introductory Dynamical Oceanography Pergamon Press Sydney. ISBN 0-08-028728-X Examples
>>> # Data from Unesco Tech. Paper in Marine Sci. No. 44, p22. >>> import seawater as sw >>> from seawater.library import T90conv >>> s = [[0, 1, 2], [15, 16, 17], [30, 31, 32], [35, 35, 35]] >>> t = T90conv([[15]*3]*4) >>> p = [[0], [250], [500], [1000]] >>> sw.svan(s, t, p) array([[ 2.82371949e-05, 2.74626498e-05, 2.66921126e-05], [ 1.68453274e-05, 1.60993333e-05, 1.53543515e-05], [ 5.80768118e-06, 5.07784980e-06, 4.34876387e-06], [ 2.30490099e-06, 2.30490099e-06, 2.30490099e-06]])
-
seawater.geostrophic.gpan(s, t, p)¶ Geopotential Anomaly calculated as the integral of svan from the the sea surface to the bottom. THUS RELATIVE TO SEA SURFACE.
Adapted method from Pond and Pickard (p76) to calculate gpan relative to sea surface whereas Pond and Pickard calculated relative to the deepest common depth. Note that older literature may use units of “dynamic decimeter” for above.
Parameters: s(p) : array_like
salinity [psu (PSS-78)]
t(p) : array_like
temperature [℃ (ITS-90)]
p : array_like
pressure [db].
Returns: gpan : array_like
geopotential anomaly [m 3 kg -1 Pa = m 2 s -2 = J kg -1]
References
[R34] S. Pond & G.Pickard 2nd Edition 1986 Introductory Dynamical Oceanography Pergamon Press Sydney. ISBN 0-08-028728-X Examples
>>> # Data from Unesco Tech. Paper in Marine Sci. No. 44, p22. >>> import seawater as sw >>> s = [[0, 1, 2], [15, 16, 17], [30, 31, 32], [35,35,35]] >>> t = [[15]*3]*4 >>> p = [[0], [250], [500], [1000]] >>> sw.gpan(s, t, p) array([[ 0. , 0. , 0. ], [ 56.35465209, 54.45399428, 52.55961152], [ 84.67266947, 80.92724333, 77.19028933], [ 104.95799186, 99.38799979, 93.82834339]])
-
seawater.geostrophic.gvel(ga, lat, lon)¶ Calculates geostrophic velocity given the geopotential anomaly and position of each station.
Parameters: ga : array_like
geopotential anomaly relative to the sea surface.
lat : array_like
latitude of each station (+ve = N, -ve = S) [ -90.. +90]
lon : array_like
longitude of each station (+ve = E, -ve = W) [-180..+180]
Returns: vel : array_like
geostrophic velocity relative to the sea surface. Dimension will be MxN-1 (N: stations)
References
[R35] S. Pond & G.Pickard 2nd Edition 1986 Introductory Dynamical Oceanography Pergamon Press Sydney. ISBN 0-08-028728-X Examples
>>> import numpy as np >>> import seawater as sw >>> lon = np.array([-30, -30, -30, -30, -30]) >>> lat = np.linspace(-22, -21, 5) >>> t = np.array([[0, 0, 0, 0, 0], ... [10, 10, 10, 10, 10], ... [20, 20, 20, 20, 20], ... [30, 30, 30, 30, 30], ... [40, 40, 40, 40, 40]]) >>> s = np.array([[25, 25, 25, 35, 35], ... [25, 25, 25, 35, 35], ... [25, 25, 25, 35, 35], ... [25, 25, 25, 35, 35], ... [25, 25, 25, 35, 35]]) >>> p = np.array([[0, 5000, 10000, 0, 5000], ... [0, 5000, 10000, 0, 5000], ... [0, 5000, 10000, 0, 5000], ... [0, 5000, 10000, 0, 5000], ... [0, 5000, 10000, 0, 5000]]) >>> ga = sw.gpan(s, t, p) >>> sw.gvel(ga, lat, lon) array([[ 231.74785186, 197.54291221, -436.64938045, 0. ], [ 231.74785186, 197.54291221, -436.64938045, 0. ], [ 231.74785186, 197.54291221, -436.64938045, 0. ], [ 231.74785186, 197.54291221, -436.64938045, 0. ], [ 231.74785186, 197.54291221, -436.64938045, 0. ]])