seapy.couplings.couplingpointstructural.CouplingPointStructural

class seapy.couplings.couplingpointstructural.CouplingPointStructural(name, system, **properties)

Bases: seapy.couplings.coupling.Coupling

Model of a point coupling between structural components.

__init__(name, system, **properties)

Constructor.

Parameters:

• name (string) – Identifier
• junction (seapy.junctions.junction) – junction
• subsystem_from (seapy.subsystems.Subsystem) – subsystem from
• subsystem_to (seapy.subsystems.Subsystem) – subsystem_to

Methods

__init__(name, system, **properties)	Constructor.
CouplingPointStructural.df
disable([subsystems])	Disable this coupling.
enable([subsystems])	Enable this coupling.
info([attributes])	Return dataframe.
plot(quantity[, yscale])	Plot quantity.

Attributes

SORT	str(object=’‘) -> str
classname	Name of class of the object.
clf	Coupling loss factor.
enabled	Switch indicating whether the object is enabled.
frequency	Frequency.
impedance_from	Choses the right impedance of subsystem_from.
impedance_to	Choses the right impedance of subsystem_from.
included	Indicates whether the object is included in the analysis.
junction
mobility_from	Mobility of subsystem_from corrected for the type of coupling.
mobility_to	Mobility of subsystem_to corrected for the type of coupling.
modal_coupling_factor	Modal coupling factor of the coupling.
name
reciproce	Reciproce or inverse coupling.
resistance_from	Resistance of subsystem_from corrected for the type of coupling.
resistance_to	Resistance of subsystem_to corrected for the type of coupling.
subsystem_from
subsystem_to
tau	Frequency averaged transmission coefficient

clf

Coupling loss factor.

impedance_from

Choses the right impedance of subsystem_from. Applies boundary conditions correction as well.

impedance_to

Choses the right impedance of subsystem_from. Applies boundary conditions correction as well.

tau

Frequency averaged transmission coefficient

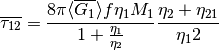
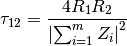
See :cite:`1998:lyon`.