Fuzzy Control Systems: The Tipping Problem¶

The Tipping Problem¶

Let’s create a fuzzy control system which models how you might choose to tip at a restaurant. When tipping, you consider the service and food quality, rated between 0 and 10. You use this to leave a tip of between 0 and 25%.

We would formulate this problem as:

• Antecednets (Inputs)

  • service

    • Universe (ie, crisp value range): How good was the service of the wait staff, on a scale of 0 to 10?
    • Fuzzy set (ie, fuzzy value range): poor, acceptable, amazing

  • food quality

    • Universe: How tasty was the food, on a scale of 0 to 10?
    • Fuzzy set: bad, decent, great

• Consequents (Outputs)

  • tip

    • Universe: How much should we tip, on a scale of 0% to 25%
    • Fuzzy set: low, medium, high

• Rules

  • IF the service was good or the food quality was good, THEN the tip will be high.
  • IF the service was average, THEN the tip will be medium.
  • IF the service was poor and the food quality was poor THEN the tip will be low.

• Usage

  • If I tell this controller that I rated:

    • the service as 9.8, and
    • the quality as 6.5,

  • it would recommend I leave:

    • a 20.2% tip.

Creating the Tipping Controller Using the skfuzzy control API¶

We can use the skfuzzy control system API to model this. First, let’s define fuzzy variables

import numpy as np
import skfuzzy as fuzz
from skfuzzy import control as ctrl

# New Antecedent/Consequent objects hold universe variables and membership
# functions
quality = ctrl.Antecedent(np.arange(0, 11, 1), 'quality')
service = ctrl.Antecedent(np.arange(0, 11, 1), 'service')
tip = ctrl.Consequent(np.arange(0, 26, 1), 'tip')

# Auto-membership function population is possible with .automf(3, 5, or 7)
quality.automf(3)
service.automf(3)

# Custom membership functions can be built interactively with a familiar,
# Pythonic API
tip['low'] = fuzz.trimf(tip.universe, [0, 0, 13])
tip['medium'] = fuzz.trimf(tip.universe, [0, 13, 25])
tip['high'] = fuzz.trimf(tip.universe, [13, 25, 25])

To help understand what the membership looks like, use the view methods.

# You can see how these look with .view()
quality['average'].view()

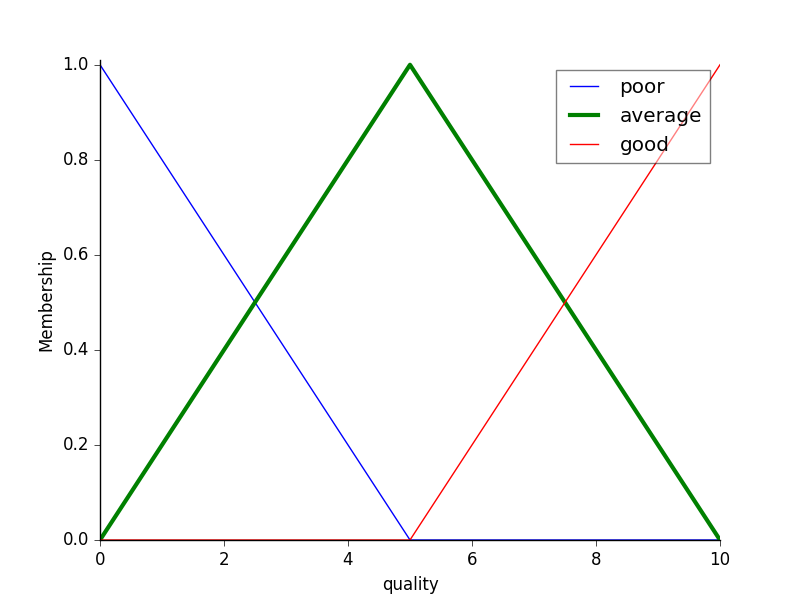
service.view()

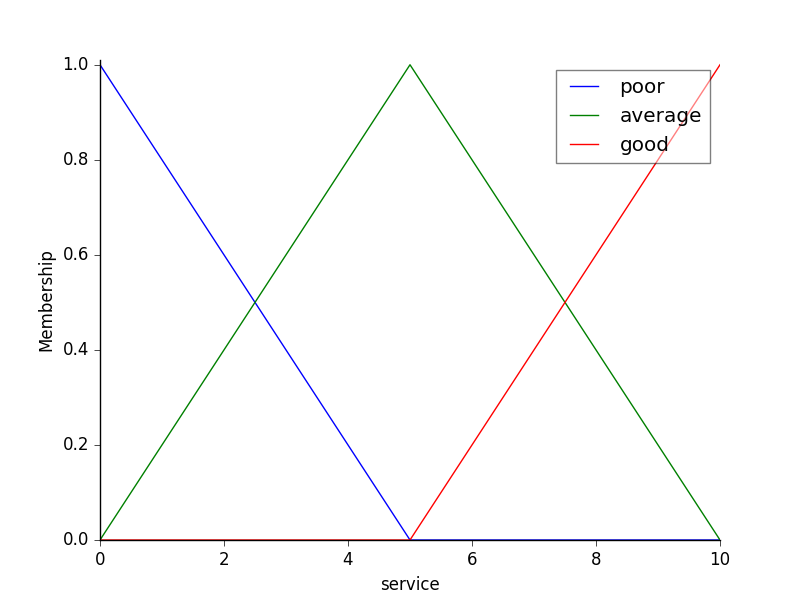
tip.view()

Fuzzy rules¶

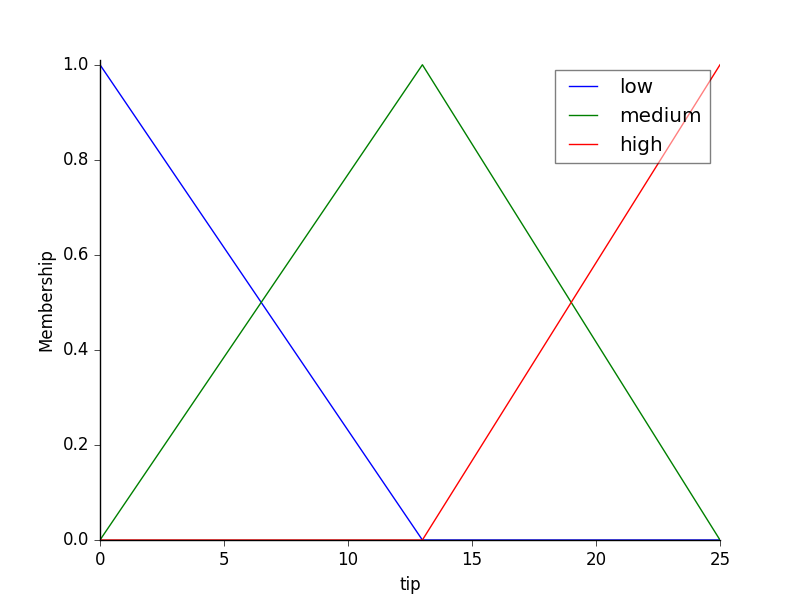
Now, to make these triangles useful, we define the fuzzy relationship between input and output variables. For the purposes of our example, consider three simple rules:

1. If the food is poor OR the service is poor, then the tip will be low
2. If the service is average, then the tip will be medium
3. If the food is good OR the service is good, then the tip will be high.

Most people would agree on these rules, but the rules are fuzzy. Mapping the imprecise rules into a defined, actionable tip is a challenge. This is the kind of task at which fuzzy logic excels.

rule1 = ctrl.Rule(quality['poor'] | service['poor'], tip['low'])
rule2 = ctrl.Rule(service['average'], tip['medium'])
rule3 = ctrl.Rule(service['good'] | quality['good'], tip['high'])

rule1.view()

Control System Creation and Simulation¶

Now that we have our rules defined, we can simply create a control system via:

tipping_ctrl = ctrl.ControlSystem([rule1, rule2, rule3])

In order to simulate this control system, we will create a ControlSystemSimulation. Think of this object representing our controller applied to a specific set of cirucmstances. For tipping, this might be tipping Sharon at the local brew-pub. We would create another ControlSystemSimulation when we’re trying to apply our tipping_ctrl for Travis at the cafe because the inputs would be different.

tipping = ctrl.ControlSystemSimulation(tipping_ctrl)

We can now simulate our control system by simply specifying the inputs and calling the compute method. Suppose we rated the quality 6.5 out of 10 and the service 9.8 of 10.

# Pass inputs to the ControlSystem using Antecedent labels with Pythonic API
# Note: if you like passing many inputs all at once, use .inputs(dict_of_data)
tipping.input['quality'] = 6.5
tipping.input['service'] = 9.8

# Crunch the numbers
tipping.compute()

Once computed, we can view the result as well as visualize it.

print tipping.output['tip']
tip.view(sim=tipping)

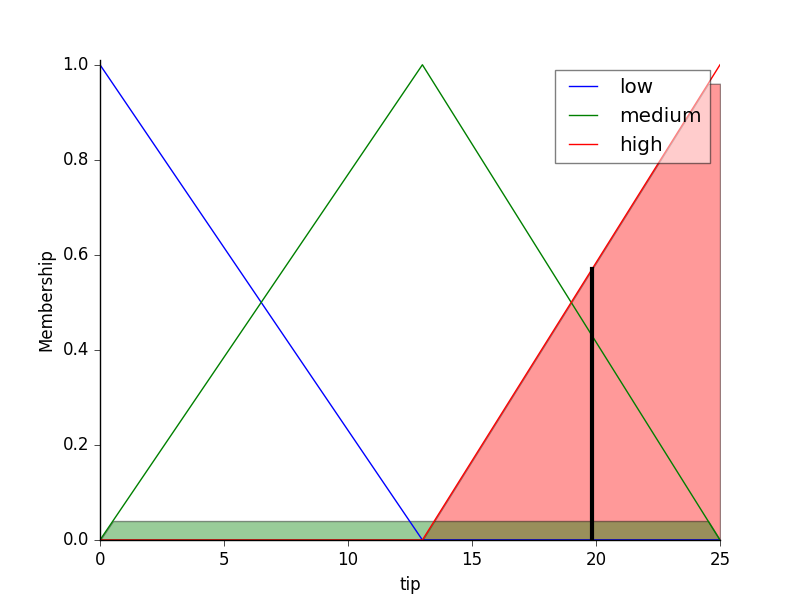
The resulting suggested tip is 20.24%.

Final thoughts¶

The power of fuzzy systems is allowing complicated, intuitive behavior based on a sparse system of rules with minimal overhead. Note our membership function universes were coarse, only defined at the integers, but fuzz.interp_membership allowed the effective resolution to increase on demand. This system can respond to arbitrarily small changes in inputs, and the processing burden is minimal.

Python source code: download (generated using skimage 0.2)