Tutorial

Example: Completing Partial Latin Squares

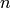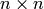A partial latin square of is a array with at most one symbol from 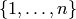in every row and every column.

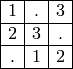
To create a partial latin square object we use a dictionary mapping cell labels to symbols.

>>> import ryser
>>> P = {1: 1, 3: 3, 4: 2, 5: 3, 8: 1, 9: 2}
>>> L = ryser.designs.Latin(P, 3)
>>> L
|1|.|3|
|2|3|.|
|.|1|2|

Completing a partial latin square means filling the empty cells so that every row and column has exactly one of every symbol. In Ryser completion of partial latin squares is handled by the completion.complete function.

>>> ryser.completion.complete(L)
|1|2|3|
|2|3|1|
|3|1|2|

Example: Hall Numbers

Here is a demo which computes Hall numbers.

>>> L = ryser.examples.eg3
>>> L
|2|1|3|4|.|.|.|.|
|1|3|2|6|.|.|.|.|
|3|2|4|1|.|.|.|.|
|4|6|1|5|.|.|.|.|
|.|.|.|.|.|1|.|.|
|.|.|.|.|1|.|.|.|
|.|.|.|.|.|.|.|2|
|.|.|.|.|.|.|2|.|
>>> S = ryser.examples.fail4[0]
>>> hall_nums = ryser.hall.numbers(L, S)
>>> sym_hall_nums = ryser.hall.symmetric_numbers(L, S)
>>> print "Hall Numbers: {}".format(hall_nums)
Hall Numbers: [0, 1, 3, 3, 4, 4, 4, 4]
>>> print "Symmetric Hall Numbers: {}".format(sym_hall_nums)
Symmetric Hall Numbers: [0, 1, 2, 2, 3, 3, 4, 4]

Test Hall inequalities.

>>> ryser.hall.inequality_on_cells(L, S)
True
>>> ryser.hall.symmetric_inequality_on_cells(L, S)
False