Diffractometer¶
This class provides the transformation from the setting angles of a six circle diffractometer into reciprocal space. There for we use mainly four frames in reciprocal Space: 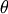 -frame,
-frame, 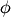 -frame,
-frame, 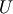 -frame and
-frame and 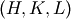 -frame.
-frame.
Lab Frame¶
We define the lab frame 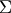 like in the paper about the four circle diffraction setup (Busing1967), i.e. the
like in the paper about the four circle diffraction setup (Busing1967), i.e. the 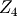 -axis up, the
-axis up, the 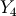 -axis along the X-ray beam and the
-axis along the X-ray beam and the 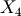 -axis forms a right handed orthonganl system with the others. The figure shows the setup with all six angles and a diffrent lab frame from the paper Lohmeier1993 (
-axis forms a right handed orthonganl system with the others. The figure shows the setup with all six angles and a diffrent lab frame from the paper Lohmeier1993 (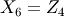 ,
, 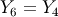 ,
, 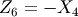 ).
).
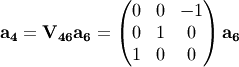
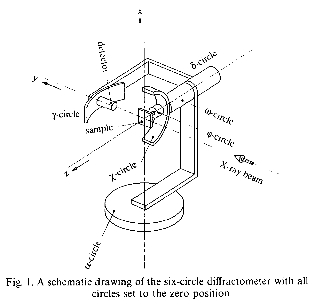
Rotations and Setting Angles¶
The rotation by 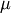 along the
along the 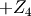 -axis leads to
-axis leads to 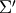 followed by the angles familiar from the four circle setup, i.e.
rotation by
followed by the angles familiar from the four circle setup, i.e.
rotation by 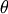 along the
along the 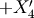 -axis leads to
-axis leads to 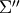 (
(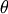 -frame,
-frame, 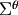 ),
rotation by
),
rotation by 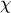 along the
along the 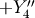 -axis leads to
-axis leads to 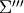 , and
rotation by
, and
rotation by 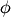 along the
along the 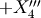 -axis leads to
-axis leads to 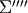 (
(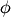 -frame,
-frame, 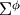 )
The detector rotations start in
)
The detector rotations start in 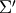 with
rotation by
with
rotation by 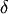 along the
along the 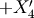 -axis into
-axis into 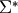 , and
rotation by
, and
rotation by 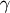 along the
along the 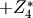 -axis into
-axis into 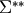 .
Note that in the origanal paper
.
Note that in the origanal paper 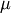 is called
is called 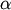 .
After this introduction we will drop most times the indices at the axes and refer to the four circle lab frame.
.
After this introduction we will drop most times the indices at the axes and refer to the four circle lab frame.
| Angle | Axis4 | Axis6 | New Frame |
|---|---|---|---|
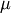 |
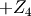 |
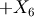 |
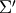 |
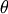 |
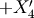 |
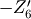 |
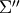 ( (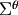 ) ) |
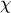 |
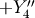 |
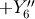 |
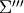 |
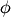 |
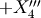 |
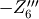 |
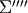 ( (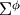 ) ) |
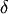 |
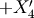 |
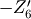 |
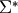 |
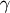 |
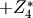 |
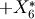 |
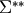 |
Rotation matrcies¶
Rotation of a vector 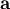 along the
along the 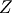 -axis by the angle
-axis by the angle 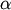 is discribed by the rotaion matrix
is discribed by the rotaion matrix 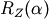
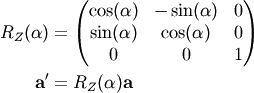
The back transformation is the transposed 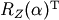 or
or 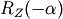 , the back rotation. If the coordinate system is rotated by the angle
, the back rotation. If the coordinate system is rotated by the angle 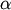 ,
, 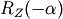 is the transformation.
For completness the other two rotation matrices along the principle axes.
is the transformation.
For completness the other two rotation matrices along the principle axes.
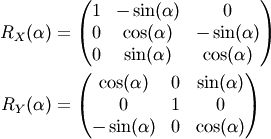
Calculation of  ¶
¶
The initial and final (scattered) wavevectors are 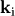 ,
, 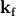 and have the same length
and have the same length 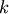 (elastic scattering).
For all setting angels set to 0,
(elastic scattering).
For all setting angels set to 0, 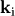 and
and 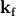 lay along the
lay along the 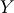 -axis.
-axis.
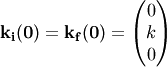
To get  , i.e. in
, i.e. in  , we have to apply the rotation matrix along
, we have to apply the rotation matrix along 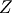 by the angle
by the angle 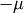 and the rotation matrix along
and the rotation matrix along 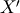 by the angle
by the angle 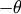 , because
, because 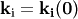 for all angles. To get
for all angles. To get 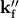 we have to considered that
we have to considered that 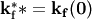 for all angles, becuase the measured scattered X-rays hit directly the detector. In a similar sence we need rotations by
for all angles, becuase the measured scattered X-rays hit directly the detector. In a similar sence we need rotations by 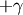 along
along 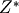 and by
and by 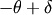 along
along 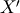 .
.
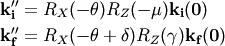
Now we get 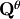 in
in 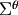 .
.
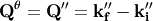
If we take the rotations by 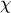 and
and 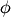 into account we come to
into account we come to 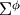 .
.
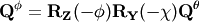
The last step is transforming from 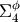 to
to 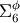 and applying the inverse orientation matrix
and applying the inverse orientation matrix 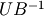 from e.g. Spec SIXC to get the
from e.g. Spec SIXC to get the 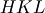 -values.
-values.
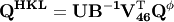
Diffractometer Class¶
- class pyspec.diffractometer.Diffractometer(mode='sixc')¶
Diffractometer class
This class provides various functions to perform calculations to and from the sample and instrument frames
used lab frame: Z up, Y along X-ray beam, X = Y x Z; sample rotations: mu : along +Z -> S’ (mu-frame), theta : along +X’ -> S’’ (theta-frame), chi : along +Y’’ -> S’‘’ (chi-frame), phi : along +X’‘’ -> S’‘’’ (phi-frame); detector rotations: mu : along +Z -> S’ (mu-frame), delta : along +X’ -> S* (delta-frame), gamma : along +Z* -> S** (gamma-frame)
- getQCart()¶
Calculate (Qx, Qy, Qz) set in cartesian reciprocal space from (Qx, Qy, Qz) set in theta-frame
still under construction
- getQHKL()¶
Calc HKL values from (Qx, Qy, Qz) set in theta-frame with UB-matrix
QHKL = UB^-1 sixcToFourc^T QPhi
- getQPhi()¶
Calculate (Qx, Qy, Qz) set in phi-frame from (Qx, Qy, Qz) set in theta-frame
QPhi = rotZ(-phi) rotY(-chi) QTheta
- getQTheta()¶
Return transformed coordinates
- setAllAngles(angles, mode='deg')¶
Sets angles for calculation. Angles are expected in spec ‘sixc’ order: Delta Theta Chi Phi Mu Gamma
- setAngles(delta=None, theta=None, chi=None, phi=None, mu=None, gamma=None, mode='deg')¶
Set the angles for calculation
- setEnergy(energy)¶
Set the energy (in eV) for calculations
- setLambda(waveLen)¶
Set the wavelength (in Angstroms) for calculations
- setUbMatrix(UBmat)¶
Sets the UB matrix