Reference¶
This is the class and function reference of cyipopt. Please refer to the tutorial for further details, as the class and function raw specifications may not be enough to give full guidelines on their uses.
- class ipopt.problem¶
Wrapper class for solving optimization problems using the C interface of the IPOPT package.
It can be used to solve general nonlinear programming problems of the form:
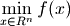
subject to
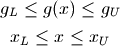
Where
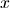 are the optimization variables (possibly with upper an lower
bounds),
are the optimization variables (possibly with upper an lower
bounds), 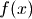 is the objective function and
is the objective function and 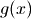 are the general nonlinear
constraints. The constraints,
are the general nonlinear
constraints. The constraints, 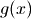 , have lower and upper bounds. Note that
equality constraints can be specified by setting
, have lower and upper bounds. Note that
equality constraints can be specified by setting 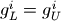 .
.Parameters : n : integer
Number of primal variables.
m : integer
Number of constraints
problem_obj: object :
An object with the following attributes (holding the problam’s callbacks)
- ‘objective’ : function pointer
Callback function for evaluating objective function. The callback functions accepts one parameter: x (value of the optimization variables at which the objective is to be evaluated). The function should return the objective function value at the point x.
- ‘constraints’ : function pointer
Callback function for evaluating constraint functions. The callback functions accepts one parameter: x (value of the optimization variables at which the constraints are to be evaluated). The function should return the constraints values at the point x.
- ‘gradient’ : function pointer
Callback function for evaluating gradient of objective function. The callback functions accepts one parameter: x (value of the optimization variables at which the gradient is to be evaluated). The function should return the gradient of the objective function at the point x.
- ‘jacobian’ : function pointer
Callback function for evaluating Jacobian of constraint functions. The callback functions accepts one parameter: x (value of the optimization variables at which the jacobian is to be evaluated). The function should return the values of the jacobian as calculated using x. The values should be returned as a 1-dim numpy array (using the same order as you used when specifying the sparsity structure)
- ‘jacobianstructure’ : function pointer
Optional. Callback function that accepts no parameters and returns the sparsity structure of the Jacobian (the row and column indices only). If None, the Jacobian is assumed to be dense.
- ‘hessian’ : function pointer
Optional. Callback function for evaluating Hessian of the Lagrangian function. The callback functions accepts three parameters x (value of the optimization variables at which the hessian is to be evaluated), lambda (values for the constraint multipliers at which the hessian is to be evaluated) objective_factor the factor in front of the objective term in the Hessian. The function should return the values of the Hessian as calculated using x, lambda and objective_factor. The values should be returned as a 1-dim numpy array (using the same order as you used when specifying the sparsity structure). If None, the Hessian is calculated numerically.
- ‘hessianstructure’ : function pointer
Optional. Callback function that accepts no parameters and returns the sparsity structure of the Hessian of the lagrangian (the row and column indices only). If None, the Hessian is assumed to be dense.
- ‘intermediate’ : function pointer
Optional. Callback function that is called once per iteration (during the convergence check), and can be used to obtain information about the optimization status while IPOPT solves the problem. If this callback returns False, IPOPT will terminate with the User_Requested_Stop status. The information below corresponeds to the argument list passed to this callback:
- ‘alg_mod’:
Algorithm phase: 0 is for regular, 1 is restoration.
- ‘iter_count’:
The current iteration count.
- ‘obj_value’:
The unscaled objective value at the current point
- ‘inf_pr’:
The scaled primal infeasibility at the current point.
- ‘inf_du’:
The scaled dual infeasibility at the current point.
- ‘mu’:
The value of the barrier parameter.
- ‘d_norm’:
The infinity norm (max) of the primal step.
- ‘regularization_size’:
The value of the regularization term for the Hessian of the Lagrangian in the augmented system.
- ‘alpha_du’:
The stepsize for the dual variables.
- ‘alpha_pr’:
The stepsize for the primal variables.
- ‘ls_trials’:
The number of backtracking line search steps.
more information can be found in the following link: http://www.coin-or.org/Ipopt/documentation/node56.html#sec:output
lb : array-like, shape = [n]
Lower bounds on variables, where n is the dimension of x. To assume no lower bounds pass values lower then 10^-19.
ub : array-like, shape = [n]
Upper bounds on variables, where n is the dimension of x.. To assume no upper bounds pass values higher then 10^-19.
cl : array-like, shape = [m]
Lower bounds on constraints, where m is the number of constraints. Equality constraints can be specified by setting cl[i] = cu[i].
cu : array-like, shape = [m]
Upper bounds on constraints, where m is the number of constraints. Equality constraints can be specified by setting cl[i] = cu[i].
- addOption()¶
Add a keyword/value option pair to the problem. See the IPOPT documentaion for details on available options.
Parameters : keyword : string,
Option name.
val : string / int / float
Value of the option. The type of val should match the option definition as described in the IPOPT documentation.
Returns : None :
- close()¶
Deallcate memory resources used by the IPOPT package. Called implicitly by the ‘problem’ class destructor.
Parameters : None : Returns : None :
- setProblemScaling()¶
Optional function for setting scaling parameters for the problem. To use the scaling parameters set the option ‘nlp_scaling_method’ to ‘user-scaling’.
Parameters : obj_scaling : float,
Determines, how IPOPT should internally scale the objective function. For example, if this number is chosen to be 10, then IPOPT solves internally an optimization problem that has 10 times the value of the original objective. In particular, if this value is negative, then IPOPT will maximize the objective function instead of minimizing it.
x_scaling : array-like, shape = [n]
The scaling factors for the variables. If None, no scaling is done.
g_scaling : array-like, shape = [m]
The scaling factors for the constrains. If None, no scaling is done.
Returns : None :
- solve()¶
Solve the posed optimization problem starting at point x. Returns the optimal solution and an info dictionary.
Parameters : x : array-like, shape = [n]
Starting point.
Returns : x : array, shape = [n]
Optimal solution.
info: dictionary, with following keys :
- ‘x’:
optimal solution
- ‘g’:
constraints at the optimal solution
- ‘obj_val’:
objective value at optimal solution
- ‘mult_g’:
final values of the constraint multipliers
- ‘mult_x_L’:
bound multipliers at the solution
- ‘mult_x_U’:
bound multipliers at the solution
- ‘status’:
gives the status of the algorithm
- ‘status_msg’:
gives the status of the algorithm as a message