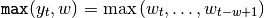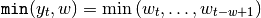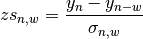Functions¶

This section lists all the functions available within the domain specific language. Each function can be called stand-alone or in combination with other others as long as the grammar of the language is respected.

In the following list we assume the following shortcuts:

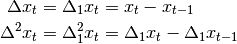
$\Delta x_t &= \Delta_1 x_t = x_t - x_{t-1}\\ \Delta^2 x_t &= \Delta_1^2 x_t = \Delta_1 x_t - \Delta_1 x_{t-1}$

The function documentation is build from the source code, using the sphinx macro dyntslist defined in dynts.web.dyntsx.

alsharpe - Annualised volatility¶

a

asharpe - Annualised volatility¶

a

avol - annualised volatility¶

a

delta¶

First order differencing evaluated as

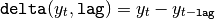
${\tt delta}(y_t,{\tt lag}) = y_t - y_{t-{\tt lag}}$

Typical usage:

delta(tiker)
delta(tiker,lag=5)

Or for calculating standard deviation on changes:

sd(delta(tiker))

parameter lag:	backward lag. Default `1`.

delta2¶

Second order difference evaluated as

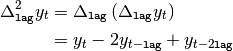
$\Delta_{\tt lag}^2 y_t &= \Delta_{\tt lag} \left( \Delta_{\tt lag} y_t \right)\\ &= y_t - 2 y_{t-{\tt lag}} + y_{t-2{\tt lag}}$

Typical usage:

delta2(tiker)
delta2(tiker,lag=5)

It is an optimised shortcut function equivalent to:

delta(delta(tiker))
delta(delta(tiker,lag=5),lag=5)

parameter lag:	backward lag. Default `1`.

ldelta - log delta¶

Calculate the logarithmic difference of a timeseries. This is the first order difference in log-space useful for evaluating percentage moments:

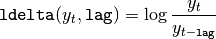
${\tt ldelta} (y_t, {\tt lag}) = \log{\frac{y_t}{y_{t-{\tt lag}}}}$

Typical usage:

ldelta(tiker)
ldelta(tiker,lag=5)

parameter lag:	backward lag. Default `1`.

log¶

Calculate the natural logarithm of a timeseries. It applies to each value and return a timeseries with exactly the same dimensions.

ma - arithmetic moving avarage¶

Arithmetic moving average function simply defined by

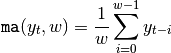
${\tt ma}(y_t,w) = \frac{1}{w}\sum_{i=0}^{w-1} y_{t-i}$

parameter window `w`:
	the rolling window in units. Default `20`

max¶

Moving max function.

${\tt max}(y_t,w) = \max\left(w_t,\dots,w_{t-w+1}\right)$

parameter window `w`:
	the rolling window in units. Default `20`

med¶

Moving median function.

min¶

Moving min function.

${\tt min}(y_t,w) = \min\left(w_t,\dots,w_{t-w+1}\right)$

parameter window `w`:
	the rolling window in units. Default `20`

prange¶

Rolling Percentage range function.

psdd - log standard deviation¶

This is a shortcut function for calculating the standard deviation of log-changes. Therefore:

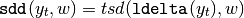
${\tt sdd}(y_t,w) = { t sd}({\tt ldelta}(y_t),w)$

regr - rolling linear regression¶

Calculate the linear regression of one series with respect to one or more series. For example:

regr(GOOG,YHOO)

will calculate

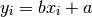
$y_i = b x_i + a$

There are two optional parameters:

alpha default is 1. If set to zero alpha won’t be included in the regression.

scatter¶

A two-dimensional scatter for timeseries:

scatter(GOOG,YHOO)

will create Google versus Yahoo prices withe date reference.

sd¶

Rolling standard deviation given by:

${\tt sd}(y_t,w) = \sqrt{{\tt scale} \cdot {\tt var}(y_t,w)}$

where var is the rolling variance (not in docs yet). Typical usage:

sd(tiker)
sd(tiker,window=40)
sd(tiker, window=40, scale = 252)
sd(ldelta(GOOG), window = 60, scale = 252)

parameter window:
	the rolling window in units. Default `20`
parameter scale:
	Scaling constant. Default `1`

sdd - standard deviation of changes¶

This is a shortcut function for calculating the standard deviation of changes. Therefore:

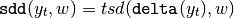
${\tt sdd}(y_t,w) = { t sd}({\tt delta}(y_t),w)$

sharpe¶

Rolling Annualised Sharpe Ratio given by:

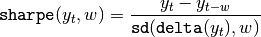
${\tt sharpe}(y_t,w) = \frac{y_t-y_{t-w}}{{\tt sd}({\tt delta}(y_t),w)}$

Typical usage:

sharpe(tiker)
sharpe(tiker,window=40)

parameter window:
	the rolling window in units. Default `20`.

sqrt¶

Calculate the square root of a timeseries. It applies to each value and return a timeseries with exactly the same dimensions.

square¶

Calculate the square of a timeseries. It applies to each value and return a timeseries with exactly the same dimensions.

var - rolling variance¶

Rolling arithmetic average variance given by:

${\tt var}(y_t,w,d) = \frac{1}{w-d} \sum_{i=0}^{w-1} \left[y_{t-i} - {\tt ma}(y_t,w)\right]^2$

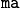where $\tt ma$ is the rolling moving average. Typical usage:

var(tiker)
var(tiker,window=40)

parameter window `w`:
	The rolling window in units. Default `20`
parameter ddof `d`:
	Delta degree of freedom. Default `0`

vol - Annualised volatility¶

a

zscore¶

Rolling Z-Score function:

$zs_{n,w} = \frac{y_n - y_{n-w}}{\sigma_{n,w}}$

Functions¶

alsharpe - Annualised volatility¶

asharpe - Annualised volatility¶

avol - annualised volatility¶

delta¶

delta2¶

ldelta - log delta¶

log¶

ma - arithmetic moving avarage¶

max¶

med¶

min¶

prange¶

psdd - log standard deviation¶

regr - rolling linear regression¶

scatter¶

sd¶

sdd - standard deviation of changes¶

sharpe¶

sqrt¶

square¶

var - rolling variance¶

vol - Annualised volatility¶

zscore¶

Table Of Contents

Previous topic

Next topic

This Page

Navigation

Functions¶

alsharpe - Annualised volatility¶

asharpe - Annualised volatility¶

avol - annualised volatility¶

delta¶

delta2¶

ldelta - log delta¶

log¶

ma - arithmetic moving avarage¶

max¶

med¶

min¶

prange¶

psdd - log standard deviation¶

regr - rolling linear regression¶

scatter¶

sd¶

sdd - standard deviation of changes¶

sharpe¶

sqrt¶

square¶

var - rolling variance¶

vol - Annualised volatility¶

zscore¶

Table Of Contents

Previous topic

Next topic

This Page

Quick search

Navigation