Consistent Overhead Byte Stuffing—Reduced (COBS/R)¶
| Author: | Craig McQueen |
|---|---|
| Contact: | http://craig.mcqueen.id.au/ |
| Copyright: | 2010 Craig McQueen |
This describes a modification of COBS, which I’m calling “Consistent Overhead Byte Stuffing—Reduced” (COBS/R). Its purpose is to save one byte from the encoded form in some cases. Plain COBS encoding always has a +1 byte encoding overhead [C1]. This is possibly undesirable, particularly in a system that encodes mostly small messages, where the +1 byte overhead would impose a noticeable increase in the bandwidth requirements.
“Base Adaptation Byte Stuffing” (BABS) is one proposal to avoid the +1 byte overhead imposed by COBS, however BABS is computationally expensive [C2].
COBS/R is a small modification of COBS that can often avoid the +1 byte overhead of COBS, yet is computationally very simple. In terms of message encoding overhead in bytes, it is not expected to achieve performance as close to the theoretical optimum as BABS, yet it is an improvement over plain COBS encoding without any significant increase in computational complexity.
COBS/R has the following features:
- Worst-case encoding overhead is the same as COBS
- Best-case encoding overhead is zero bytes, an improvement over COBS
- Computation complexity is approximately the same as COBS, much simpler than BABS
- Same theoretical encoding delay as COBS (up to 254 bytes of temporary buffering)
- Same theoretical decoding delay as COBS (1 byte of temporary buffering)
COBS/R Encoding Modification¶
In plain COBS, the last length code byte in the message has some inherent redundancy: if it is greater than the number of remaining bytes, this is detected as an error.
In COBS/R, instead we opportunistically replace the final length code byte with the final data byte, whenever the value of the final data byte is greater than or equal to what the final length value would normally be. This variation can be unambiguously decoded: the decoder notices that the length code is greater than the number of remaining bytes.
Examples¶
The byte values in the examples are in hex.
First example:¶
Input:
| 2F | A2 | 00 | 92 | 73 | 02 |
This example is encoded the same in COBS and COBS/R. Encoded (length code bytes are bold):
| 03 | 2F | A2 | 04 | 92 | 73 | 02 |
Second example:¶
The second example is almost the same, except the final data byte value is greater than what the length byte would be.
Input:
| 2F | A2 | 00 | 92 | 73 | 26 |
Encoded in plain COBS (length code bytes are bold):
| 03 | 2F | A2 | 04 | 92 | 73 | 26 |
Encoded in COBS/R:
| 03 | 2F | A2 | 26 | 92 | 73 |
Because the last data byte (26) is greater than the usual length code (04), the last data byte can be inserted in place of the length code, and removed from the end of the sequence. This avoids the usual +1 byte overhead of the COBS encoding.
The decoder detects this variation on the encoding simply by detecting that the length code is greater than the number of remaining bytes. That situation would be a decoding error in regular COBS, but in COBS/R it is used to save one byte in the encoded message.
COBS/R Encoding Overhead¶
Given an input data packet of size n, COBS/R encoding may or may not add a +1 byte overhead, depending on the contents of the input data. The probability of the +1 byte overhead can be calculated, and hence, the average overhead can be calculated.
The calculations are more complicated for the case of message sizes greater than 254 bytes. COBS/R is of particular interest for smaller message sizes, so the calculations will focus on the simpler case of message sizes smaller than 255 bytes.
General Case¶
Example for n=4:
 |
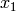 |
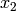 |
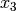 |
Probability of Pattern | Probability of +1 byte |
|---|---|---|---|---|---|
| any | any | any | 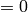 |
 |
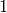 |
| any | any | 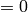 |
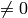 |
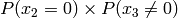 |
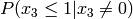 |
| any | 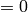 |
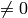 |
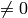 |
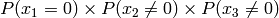 |
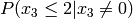 |
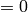 |
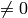 |
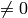 |
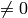 |
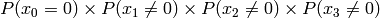 |
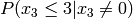 |
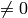 |
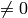 |
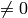 |
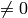 |
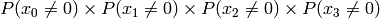 |
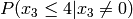 |
Multiply the last two columns, and sum for all rows. For a message of length
n where 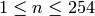 , the general equation for the
probability of the +1 byte is:
, the general equation for the
probability of the +1 byte is:
![P(x_{n-1} \le n|x_{n-1}\ne 0) \prod_{k=0}^{n-1} P(x_k\ne 0) + \sum_{i=0}^{n-2} \left[ P(x_{n-1} \le (n-1-i)|x_{n-1}\ne 0) P(x_i=0) \prod_{k=i+1}^{n-1} P(x_k\ne 0) \right] + P(x_{n-1}=0)](_images/math/b024d4ab13f2c2ddb28f2c53d0c0fabd9d5ef2a1.png)
Even Byte Distribution Case¶
We can simplify this for the simpler case of messages with byte value probabilities that are evenly distributed. In this case:
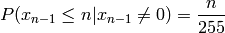
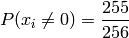
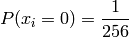
Simplified example for n=4:
 |
 |
 |
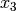 |
Probability of Pattern | Probability of +1 byte |
|---|---|---|---|---|---|
| any | any | any | 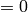 |
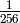 |
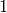 |
| any | any | 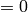 |
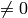 |
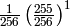 |
 |
| any | 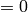 |
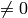 |
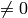 |
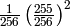 |
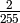 |
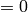 |
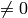 |
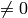 |
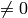 |
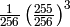 |
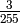 |
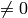 |
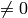 |
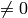 |
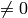 |
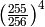 |
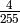 |
The simplified equation for a message of length n where
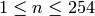 is:
is:
![\frac{n}{255} \left(\frac{255}{256}\right)^n + \frac{1}{255 \times 256} \sum_{i=1}^{n-1} \left[ i \left(\frac{255}{256}\right)^i \right] + \frac{1}{256}](_images/math/7f44c24a6d91354f1595538597c68400bb46f6b8.png)
Which simplifies to:
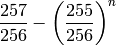
Table 1 of [C2] shows the overhead of BABS compared to COBS and PPP. We will duplicate this table up to N=128, comparing the figures for COBS/R (instead of PPP):
| N | mean(OH) BABS | mean(OH) COBS | mean(OH) COBS/R | max(OH) BABS, COBS, COBS/R |
|---|---|---|---|---|
| 1 | 0.39062 | 100 | 0.78125 | 100 |
| 2 | 0.39062 | 50 | 0.58517 | 50 |
| 4 | 0.38948 | 25 | 0.48600 | 25 |
| 8 | 0.38665 | 12.5 | 0.43415 | 12.5 |
| 16 | 0.38078 | 6.25 | 0.40380 | 6.25 |
| 32 | 0.36927 | 3.125 | 0.38008 | 3.125 |
| 64 | 0.34756 | 1.5625 | 0.35232 | 1.5625 |
| 128 | 0.30906 | 0.78125 | 0.31091 | 0.78125 |
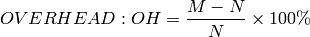
Further Observations for General Case¶
Going back to the general case, we can make several observations about what sort of byte distributions more favourably avoid the +1 byte in the COBS/R encoding.
- For all bytes except the final one, a higher probability of a zero byte value is more favourable.
- For the final byte of the message, a probability distribution that favours high byte values is more favourable.
If the byte distribution of a communication protocol is known in advance, it may be possible and worthwhile to pre-process the data bytes before COBS/R encoding, to reduce the average size of the COBS/R encoded data. For example, possible byte manipulations may be:
- For all bytes except the final one, if a particular byte value is statistically common, XOR every byte of the message (except the last byte) with that byte value.
- For the final byte of the message, add an offset to the final byte value, or negate the final byte value, to shift the distribution to favour high byte values.
Of course after decoding, the data would have to be post-processed to reverse the effects of any encoding pre-processing step.