Posterior Log Probability

We want the derivative of a posterior log probability density calculation. We have a normal distribution with known variance.

import numpy; from algopy import UTPM, zeros, Function, CGraph; import os

def LogNormalLikelihood(x, mu, sigma):
   return sigma *(x - mu)**2  - numpy.log(.5*sigma/numpy.pi)

def logp(x, mu, sigma):
    return numpy.sum(LogNormalLikelihood(x, mu, sigma)) + LogNormalLikelihood(mu , mu_prior_mean, mu_prior_sigma)

mu_prior_mean = 1
mu_prior_sigma = 5

actual_mu = 3.1
sigma = 1.2
N = 35
x = numpy.random.normal(actual_mu, sigma, size = N)
mu = UTPM([[3.5],[1],[0]]) #unknown variable

print('function evaluation =\n',logp(x,3.5,sigma))

# forward mode with ALGOPY
utp = logp(x, mu, sigma).data[:,0]
print('function evaluation = %f\n1st directional derivative = %f\n2nd directional derivative = %f'%(utp[0], 1.*utp[1], 2.*utp[2]))

# finite differences solution:
print('finite differences derivative =\n',(logp(x,3.5+10**-8,sigma) - logp(x, 3.5, sigma))/10**-8)

# trace function evaluation
cg = CGraph()
mu = Function(UTPM([[3.5],[1],[0]])) #unknown variable
out = logp(x, mu, sigma)
cg.trace_off()
cg.independentFunctionList = [mu]
cg.dependentFunctionList = [out]
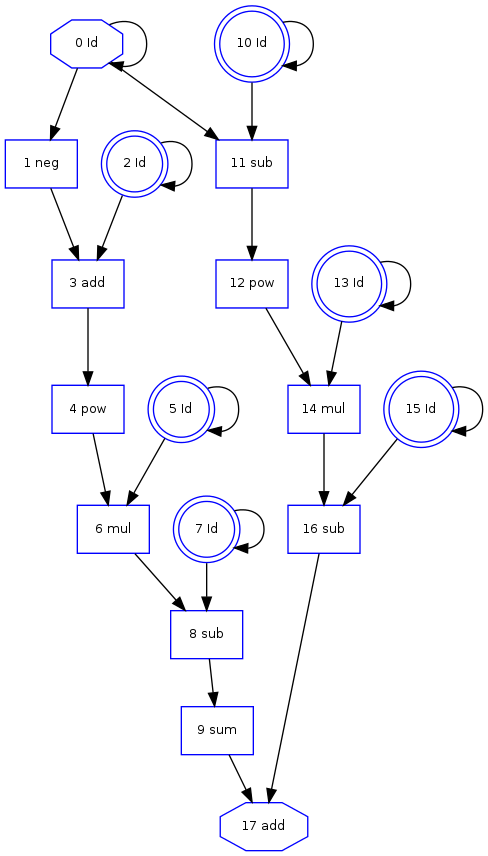
cg.plot(os.path.join(os.path.dirname(os.path.realpath(__file__)),'posterior_log_probability_cgraph.png'))

# reverse mode with ALGOPY
outbar = UTPM([[1.],[0],[0]])
cg.pullback([outbar])
    
gradient =  mu.xbar.data[0,0]
Hess_vec =  mu.xbar.data[1,0]

print('gradient = ', gradient)
print('Hessian vector product = ', Hess_vec)

as output one obtains:

walter@wronski$ python examples/posterior_log_probability.py
function evaluation =
138.692022348
function evaluation = 138.692022
1st directional derivative = 44.061288
2nd directional derivative = 94.000000
finite differences derivative =
44.0612893726
gradient =  44.0612882911
Hessian vector product =  94.0

and the computational graph: