Reliability estimation (Orange.evaluation.reliability)¶
Reliability Estimation for Regression and Classification¶
Reliability assessment aims to predict reliabilities of individual predictions. Most of the implemented algorithms for regression are described in [Bosnic2008]; the algorithms for classification are described in [Pevec2011].
We can use reliability estimation with any prediction method. The following example:
- Constructs reliability estimators (implemented in this module),
- The Learner wrapper combines a a prediction method (learner), here a kNNLearner, with reliability estimators.
- Obtains prediction probabilities, which have an additional attribute, reliability_estimate, that contains a list of Orange.evaluation.reliability.Estimate.
import Orange
housing = Orange.data.Table("housing.tab")
knn = Orange.classification.knn.kNNLearner()
estimators = [Orange.evaluation.reliability.Mahalanobis(k=3),
Orange.evaluation.reliability.LocalCrossValidation(k = 10)]
reliability = Orange.evaluation.reliability.Learner(knn, estimators = estimators)
restimator = reliability(housing)
instance = housing[0]
value, probability = restimator(instance, result_type=Orange.classification.Classifier.GetBoth)
for estimate in probability.reliability_estimate:
print estimate.method_name, estimate.estimate
The next example prints reliability estimates for first 10 instances (with cross-validation):
import Orange
housing = Orange.data.Table("housing.tab")
knn = Orange.classification.knn.kNNLearner()
reliability = Orange.evaluation.reliability.Learner(knn)
results = Orange.evaluation.testing.cross_validation([reliability], housing)
for i, instance in enumerate(results.results[:10]):
print "Instance", i
for estimate in instance.probabilities[0].reliability_estimate:
print " ", estimate.method_name, estimate.estimate
Reliability estimation wrappers¶
- class Orange.evaluation.reliability.Learner(box_learner, name='Reliability estimation', estimators=None, **kwds)¶
Adds reliability estimation to any prediction method. This class can be used as any other Orange learner, but returns the classifier wrapped into an instance of Orange.evaluation.reliability.Classifier.
Parameters: - box_learner (Learner) – Learner to wrap into a reliability estimation classifier.
- estimators (list of reliability estimators) – List of reliability estimation methods. Default (if None): SensitivityAnalysis, LocalCrossValidation, BaggingVarianceCNeighbours, Mahalanobis, MahalanobisToCenter.
- name (string) – Name of this reliability learner.
Return type:
- class Orange.evaluation.reliability.Classifier(instances, box_learner, estimators, blending, blending_domain, rf_classifier, **kwds)¶
A reliability estimation wrapper for classifiers. The returned probabilities contain an additional attribute reliability_estimate, which is a list of Estimate (see __call__).
- __call__(instance, result_type=0)¶
Classify and estimate reliability for a new instance. When result_type is set to Orange.classification.Classifier.GetBoth or Orange.classification.Classifier.GetProbabilities, an additional attribute reliability_estimate (a list of Estimate) is added to the distribution object.
Parameters: - instance (Orange.data.Instance) – instance to be classified.
- result_type – Orange.classification.Classifier.GetValue or Orange.classification.Classifier.GetProbabilities or Orange.classification.Classifier.GetBoth
Return type: Orange.data.Value, Orange.statistics.Distribution or a tuple with both
Reliability Methods¶
All measures except 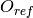 work with regression. Classification is
supported by BAGV, LCV, CNK and DENS,
work with regression. Classification is
supported by BAGV, LCV, CNK and DENS, 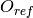 .
.
Sensitivity Analysis (SAvar and SAbias)¶
- class Orange.evaluation.reliability.SensitivityAnalysis(e=[0.01, 0.1, 0.5, 1.0, 2.0], name='sa')¶
Parameters: e (list of floats) – Values of  .
.Return type: Orange.evaluation.reliability.SensitivityAnalysisClassifier The learning set is extended with that instancem, where the label is changed to
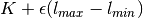 (
(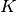 is the initial prediction,
is the initial prediction,
 a sensitivity parameter, and
a sensitivity parameter, and 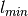 and
and
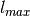 the lower and upper bounds of labels on training data).
Results for multiple values of
the lower and upper bounds of labels on training data).
Results for multiple values of  are combined
into SAvar and SAbias. SAbias has a signed or absolute form.
are combined
into SAvar and SAbias. SAbias has a signed or absolute form.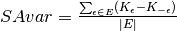
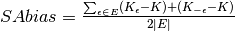
Variance of bagged models (BAGV)¶
- class Orange.evaluation.reliability.BaggingVariance(m=50, name='bv', randseed=0, for_instances=None)¶
Parameters: - m (int) – Number of bagged models. Default: 50.
- for_instances – Optional. If test instances are given as a parameter, this class can compute their reliabilities on the fly, which saves memory.
Return type: Orange.evaluation.reliability.BaggingVarianceClassifier
For regression, BAGV is the variance of predictions:
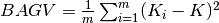 , where
, where
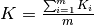 and
and 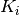 are
predictions of individual models.
are
predictions of individual models.For classification, BAGV is 1 minus the average Euclidean distance between class probability distributions predicted by the model, and distributions predicted by the individual bagged model; a greater value implies a better prediction.
This reliability measure can run out of memory if individual classifiers themselves use a lot of memory; it needs
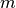 times memory
for a single classifier.
times memory
for a single classifier.
Local cross validation reliability estimate (LCV)¶
- class Orange.evaluation.reliability.LocalCrossValidation(k=0, distance=<function hellinger_dist at 0x3b9e320>, distance_weighted=True, name='lcv')¶
Parameters: - k (int) – Number of nearest neighbours used. Default: 0, which denotes 1/20 of data set size (or 5, whichever is greater).
- distance (function) – Function that computes a distance between two discrete distributions (used only in classification problems). The default is Hellinger distance.
- distance_weighted – Relevant only for classification;
use an average distance between distributions, weighted by
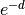 ,
where
,
where 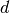 is the distance between predicted instance and the
neighbour.
is the distance between predicted instance and the
neighbour.
Return type: Orange.evaluation.reliability.LocalCrossValidationClassifier
Leave-one-out validation is performed on
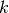 nearest neighbours to the given instance.
Reliability estimate for regression is then the distance
weighted absolute prediction error. For classification, it is 1 minus the average
distance between the predicted class probability distribution and the
(trivial) probability distributions of the nearest neighbour.
nearest neighbours to the given instance.
Reliability estimate for regression is then the distance
weighted absolute prediction error. For classification, it is 1 minus the average
distance between the predicted class probability distribution and the
(trivial) probability distributions of the nearest neighbour.
Local modeling of prediction error (CNK)¶
- class Orange.evaluation.reliability.CNeighbours(k=5, distance=<function hellinger_dist at 0x3b9e320>, name='cnk')¶
Parameters: - k (int) – Number of nearest neighbours.
- distance (function) – function that computes a distance between two discrete distributions (used only in classification problems). The default is Hellinger distance.
Return type: Orange.evaluation.reliability.CNeighboursClassifier
For regression, CNK is a difference between average label of its nearest neighbours and the prediction. CNK can be either signed or absolute. A greater value implies greater prediction error.
For classification, CNK is equal to 1 minus the average distance between predicted class distribution and (trivial) class distributions of the $k$ nearest neighbours from the learning set. A greater value implies better prediction.
Bagging variance c-neighbours (BVCK)¶
- class Orange.evaluation.reliability.BaggingVarianceCNeighbours(bagv=BaggingVariance(), cnk=CNeighbours())¶
Parameters: - bagv (BaggingVariance) – Instance of Bagging Variance estimator.
- cnk (CNeighbours) – Instance of CNK estimator.
Return type: Orange.evaluation.reliability.BaggingVarianceCNeighboursClassifier
BVCK is an average of Bagging variance and local modeling of prediction error.
Mahalanobis distance¶
- class Orange.evaluation.reliability.Mahalanobis(k=3, name='mahalanobis')¶
Parameters: k (int) – Number of nearest neighbours used in Mahalanobis estimate. Return type: Orange.evaluation.reliability.MahalanobisClassifier Mahalanobis distance reliability estimate is defined as Mahalanobis distance to the evaluated instance’s
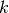 nearest neighbours.
nearest neighbours.
Mahalanobis to center¶
- class Orange.evaluation.reliability.MahalanobisToCenter(name='mahalanobis to center')¶
Return type: Orange.evaluation.reliability.MahalanobisToCenterClassifier Mahalanobis distance to center reliability estimate is defined as a Mahalanobis distance between the predicted instance and the centroid of the data.
Density estimation using Parzen window (DENS)¶
- class Orange.evaluation.reliability.ParzenWindowDensityBased(K=<function gauss_kernel at 0x3b9ede8>, d_measure=Orange.distance.Euclidean 'euclidean', name='density')¶
Parameters: - K (function) – kernel function. Default: gaussian.
- d_measure (Orange.distance.DistanceConstructor) – distance measure for inter-instance distance.
Return type: Orange.evaluation.reliability.ParzenWindowDensityBasedClassifier
Returns a value that estimates a density of problem space around the instance being predicted.
Internal cross validation (ICV)¶
- class Orange.evaluation.reliability.ICV(estimators=None, folds=10)¶
Selects the best reliability estimator for the given data with internal cross validation [Bosnic2010].
Parameters: - estimators (list of reliability estimators) – reliability estimation methods to choose from. Default (if None): SensitivityAnalysis, LocalCrossValidation, BaggingVarianceCNeighbours, Mahalanobis, MahalanobisToCenter ]
- folds – The number of fold for cross validation (default 10).
Stacked generalization (Stacking)¶
- class Orange.evaluation.reliability.Stacking(stack_learner=None, estimators=None, folds=10, save_data=False)¶
This methods develops a model that integrates reliability estimates from all available reliability scoring techniques (see [Wolpert1992] and [Dzeroski2004]). It performs internal cross-validation and therefore takes roughly the same time as ICV.
Parameters: - stack_learner (Orange.classification.Learner) – a data modelling method. Default (if None): unregularized linear regression with prior normalization.
- estimators (list of reliability estimators) – Reliability estimation methods to choose from. Default (if None): SensitivityAnalysis, LocalCrossValidation, BaggingVarianceCNeighbours, Mahalanobis, MahalanobisToCenter.
- folds – The number of fold for cross validation (default 10).
- save_data – If True, save the data used for training the integration model into resulting classifier’s .data attribute (default False).
Reference Estimate for Classification (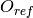 )¶
)¶
- class Orange.evaluation.reliability.ReferenceExpectedError(name='reference')¶
Return type: Orange.evaluation.reliability.ReferenceExpectedErrorClassifier Reference estimate for classification:
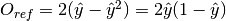 , where
, where 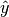 is the estimated probability of the predicted class [Pevec2011].
is the estimated probability of the predicted class [Pevec2011].A greater estimate means a greater expected error.
Reliability estimation results¶
- Orange.evaluation.reliability.SIGNED¶
- Orange.evaluation.reliability.ABSOLUTE¶
These constants distinguish signed and absolute reliability estimation measures.
- Orange.evaluation.reliability.METHOD_NAME¶
A dictionary that that maps reliability estimation method IDs (integers) to method names (strings).
- class Orange.evaluation.reliability.Estimate(estimate, signed_or_absolute, method)¶
Describes a reliability estimate.
- estimate¶
Value of reliability.
- signed_or_absolute¶
Determines whether the method returned a signed or absolute result. Has a value of either SIGNED or ABSOLUTE.
- method¶
An integer ID of the reliability estimation method used.
- method_name¶
Name (string) of the reliability estimation method used.
Reliability estimation scoring¶
- Orange.evaluation.reliability.get_pearson_r(res)¶
Parameters: res (Orange.evaluation.testing.ExperimentResults) – Evaluation results with reliability_estimate. Pearson’s coefficients between the prediction error and reliability estimates with p-values.
- Orange.evaluation.reliability.get_pearson_r_by_iterations(res)¶
Parameters: res (Orange.evaluation.testing.ExperimentResults) – Evaluation results with reliability_estimate. Pearson’s coefficients between prediction error and reliability estimates averaged over all folds.
- Orange.evaluation.reliability.get_spearman_r(res)¶
Parameters: res (Orange.evaluation.testing.ExperimentResults) – Evaluation results with reliability_estimate. Spearman’s coefficients between the prediction error and reliability estimates with p-values.
Example¶
The following script prints Pearson’s correlation coefficient (r) between reliability estimates and actual prediction errors, and a corresponding p-value, for default reliability estimation measures.
import Orange
prostate = Orange.data.Table("prostate.tab")
knn = Orange.classification.knn.kNNLearner()
reliability = Orange.evaluation.reliability.Learner(knn)
res = Orange.evaluation.testing.cross_validation([reliability], prostate)
reliability_res = Orange.evaluation.reliability.get_pearson_r(res)
print
print "Estimate r p"
for estimate in reliability_res:
print "%-21s%7.3f %7.3f" % (Orange.evaluation.reliability.METHOD_NAME[estimate[3]],
estimate[0], estimate[1])
Results:
Estimate r p
SAvar absolute -0.077 0.454
SAbias signed -0.165 0.105
SAbias absolute 0.095 0.352
LCV absolute 0.069 0.504
BVCK absolute 0.060 0.562
BAGV absolute 0.078 0.448
CNK signed 0.233 0.021
CNK absolute 0.058 0.574
Mahalanobis absolute 0.091 0.375
Mahalanobis to center 0.096 0.349
References¶
| [Bosnic2007] | Bosnić, Z., Kononenko, I. (2007) Estimation of individual prediction reliability using local sensitivity analysis. Applied Intelligence 29(3), pp. 187-203. |
| [Bosnic2008] | Bosnić, Z., Kononenko, I. (2008) Comparison of approaches for estimating reliability of individual regression predictions. Data & Knowledge Engineering 67(3), pp. 504-516. |
| [Bosnic2010] | Bosnić, Z., Kononenko, I. (2010) Automatic selection of reliability estimates for individual regression predictions. The Knowledge Engineering Review 25(1), pp. 27-47. |
| [Pevec2011] | (1, 2) Pevec, D., Štrumbelj, E., Kononenko, I. (2011) Evaluating Reliability of Single Classifications of Neural Networks. Adaptive and Natural Computing Algorithms, 2011, pp. 22-30. |
| [Wolpert1992] | Wolpert, David H. (1992) Stacked generalization. Neural Networks, Vol. 5, 1992, pp. 241-259. |
| [Dzeroski2004] | Dzeroski, S. and Zenko, B. (2004) Is combining classifiers with stacking better than selecting the best one? Machine Learning, Vol. 54, 2004, pp. 255-273. |