Example Usage¶
The Data¶
The program requires input data in the form of basic text files and a particular file system directory structure to organize the data. To use the program you will need to navigate to a directory where you have at least one directory named for a bicycle that contains parameters files or raw data measurements. Refer to the document BicycleParameters Data File Information for details about what the data files should contain.
Data Directory¶
You will need to setup a directory (a directory named data is used in the following examples) somewhere for the data input and output files. The structure of the directory should look like this:
/data
|
-->/bicycles
| |
| -->/Bicyclea
| | |
| | -->/Parameters
| | |
| | -->/Photos
| | |
| | -->/RawData
| |
| -->/Bicycleb
| |
| -->/Parameters
| |
| -->/Photos
| |
| -->/RawData
-->/riders
|
-->/Ridera
|
-->/Parameters
|
-->/RawData
Bicycle/rider name¶
A bicycle or rider name is a descriptive word (or compound word) for a bicycle or rider in which the first letter is capitalized. Examples of bicycle short names include Bianchipista, Bike, Mybike, Rigidrider, Schwintandem, Gyrobike, Bicyclea, etc. Examples of rider names include Jason, Mont, Lukepeterson, etc. The program relies on CamelCase words, so make sure the first letter is capitalized and no others are.
bicycles Directory¶
The bicycles directory contains subdirectories for each bicycle. The directory name for a bicycle should be its bicycle name. Each directory in bicycles should contain at least a RawData directory or a Parameters directory. Photos is an optional directory.
RawData directory¶
You can supply raw measurement data in two forms:
- A file containing all the manual measurements (including the oscillation periods for each rigid body). Refer to bicycles/<bicycle name>/RawData/<bicycle name>Measured.txt for details about the contents of this file.
- A file containing all the manual measurements (not including the oscillation periods for each rigid body) and a set of data files containing oscillatory signals from which the periods can be estimated. Refer to Pendulum Data Files for details about these files.
The manual measurement data file should follow the naming convention <bicycle name>Measure.txt. This data is used to generate parameter files that can be saved to the Parameters directory.
Parameters directory¶
If you don’t have any raw measurements for the bicycle it is also an option to supply a parameter file in the Parameters directory. Simply add a file named <bicycle name>Benchmark.txt with the benchmark parameter set into the Parameters directory for the particular bicycle. Refer to bicycles/<bicycle name>/Parameters/<bicycle name>Benchmark.txt for details about the contents of the file.
Photos directory¶
The Photos folder should contain photos of the bicycle parts hung as the various pendulums in the various orientations. The filename should follow the conventions of the raw signal data files.
riders directory¶
The riders directory should contain a directory for each rider that you have data for. The individual rider directory contains a Parameters for the rider inertial parameters sets and a RawData directory for the raw measurements needed for the Yeadon inertia model. Refer to riders/<rider name>/Parameters/ for details about these input files.
Example Data¶
Example data is available as a bz2 tarball or a zip file [~90mb].
Loading bicycle data¶
The easiest way to load a bicycle is:
>>> import bicycleparameters as bp
>>> bicycle = bp.Bicycle('Stratos')
This will create an instance of the Bicycle class in the variable bicycle based off of input data from the ./bicycles/Stratos/ directory. The program first looks to see if there are any parameter sets in ./bicycles/Stratos/Parameters/. If so, it loads the data, if not it looks for ./bicycles/Stratos/RawData/StratosMeasurments.txt so that it can generate the parameter set. The raw measurement file may or may not contain the oscillation period data for the bicycle moment of inertia caluclations. If it doesn’t then the program will look for the series of .mat files need to calculate the periods. If no data is there, then you get an error.
There are other loading options:
>>> bicycle = bp.Bicycle('Stratos', pathToData='<some path to the data directory>', forceRawCalc=True, forcePeriodCalc=True)
The pathToData option allows you specify a directory other than the current directory as your data directory. The forceRawCalc forces the program to load ./bicycles/Stratos/RawData/StratosMeasurments.txt and recalculate the parameters regarless if there are any parameter files available in ./bicycles/Stratos/Parameters/. The forcePeriodCalc option forces the period calcluation from the .mat files regardless if they already exist in the raw measurement file.
Exploring bicycle parameter data¶
The bicycle has a name:
>>> bicycle.bicycleName
'Stratos'
and a directory where its data is stored:
>>> bicycle.direcotory
'./bicycles/Stratos'
The benchmark bicycle parameters are the fundamental parameter set that is used behind the scenes for calculations. To access them type:
>>> bPar = bicycle.parameters['Benchmark']
>>> bPar['xB']
0.32631503794489763+/-0.0032538862692938642
The program automatically calculates the uncertainties in the parameters based on the raw measurements or the uncertainties provided in the parameter files. If you’d like to work with the pure values you can remove them:
>>> bParPure = bp.io.remove_uncertainties(bPar)
>>> bParPure['xB']
0.32631503794489763
That goes the same for all values with uncertainties. Check out the uncertainties package details for more ways to manipulate the quantities.
If the bicycle was calculated from raw data measurements you can access them by:
>>> bicycle.parameters['Measurements']
All parameter sets are stored in the parameter dictionary of the bicycle instance.
To modify a parameter type:
>>> bicycle.parameters['Benchmark']['mB] = 50.
You can regenerate the parameter sets from the raw data stored in the bicycle’s directory by calling:
>>> bicycle.calculate_from_measured()
Basic Analysis¶
The program has some basic bicycle analysis tools based on the Whipple bicycle model which has been linearized about the upright configuration.
The canonical matrices for the equations of motion can be computed:
>>> M, C1, K0, K2 = bicycle.canonical()
>>> M
array([[4.87735569387+/-0.0239343413077, 0.407911475492+/-0.00852495589396],
[0.407911475492+/-0.00852495589396,
0.203245633856+/-0.00235820505536]], dtype=object)
>>> C1
array([[0.0, 4.85200252888+/-0.0242948940194],
[-0.488808930325+/-0.00358710467251,
0.751423298199+/-0.0118190412791]], dtype=object)
>>> K0
array([[-8.1786550655+/-0.0281976329402,
-0.709791925937+/-0.013158888468],
[-0.709791925937+/-0.013158888468,
-0.206338069868+/-0.00571395841832]], dtype=object)
>>> K2
array([[0.0,
8.39212115462+/-0.0313979563061],
[0.0,
0.778591689057+/-0.0128042478172]], dtype=object))
as well as the state and input matrices for state space form at a particular speed (1.34 m/s):
>>> A, B = bicycle.state_space(1.34)
>>> A
array([[0.0, 0.0, 1.0, 0.0],
[0.0, 0.0, 0.0, 1.0],
[16.324961319+/-0.039204516678, -2.30677907291+/-0.00824125009025,
-0.323894489886+/-0.00578005141184,
-1.10401174487+/-0.00684136323415],
[1.49533216875+/-0.153839831788, 7.71036924174+/-0.170699435465,
3.8727732103+/-0.0342265538607, -2.73840155487+/-0.0133666010323]], dtype=object)
>>> B
array([[0.0, 0.0],
[0.0, 0.0],
[0.246385378456+/-0.00169761878443,
-0.494492409794+/-0.00770906162244],
[-0.494492409794+/-0.00770906162244, 5.91259504914+/-0.0401866728435]], dtype=object)
You can calculate the eigenvalues and eigenvectors at any speed by calling:
>>> w, v = bicycle.eig(4.28) # the speed should be in meters/second
>>> w # eigenvalues
array([[-6.83490195+0.j , 0.46085314+2.77336727j,
0.46085314-2.77336727j, -1.58257375+0.j ]])
>>> v # eigenvectors
array([[[ 0.04283049+0.j , 0.50596715+0.33334818j,
0.50596715-0.33334818j, 0.55478588+0.j ],
[ 0.98853840+0.j , 0.72150298+0.j ,
0.72150298+0.j , 0.63786241+0.j ],
[-0.00626644+0.j , 0.14646768-0.15809917j,
0.14646768+0.15809917j, -0.35055926+0.j ],
[-0.14463096+0.j , 0.04206844-0.25316359j,
0.04206844+0.25316359j, -0.40305383+0.j ]]])
The eig function also accepts a one dimensional array of speeds and returns eigenvalues for all speeds. Note that uncertainty propagation into the eigenvalue calculations is not supported yet.
The moment of inertia of the steer assembly (handlebar, fork and/or front wheel) can be computed either about the center of mass or a point on the steer axis, both with reference to a frame aligned with the steer axis:
>>> bicycle.steer_assembly_moment_of_inertia(aboutSteerAxis=True)
array([[0.539931205836+/-0.00362870864185, 0.0,
0.00921422347873+/-0.00191753741975],
[0.0, 0.578940852064+/-0.00311525776442, 0.0],
[0.00921422347873+/-0.00191753741975, 0.0,
0.143206097868+/-0.00100279291208]], dtype=object)
Plots¶
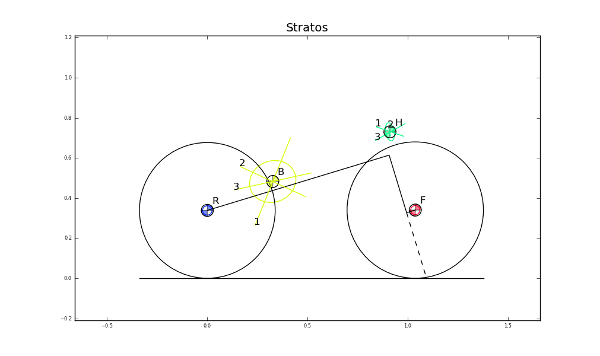
You can plot the geometry of the bicycle and include the mass centers of the various bodies, the inertia ellipsoids and the torsional pendulum axes from the raw measurement data:
>>> bicycle.plot_bicycle_geometry()
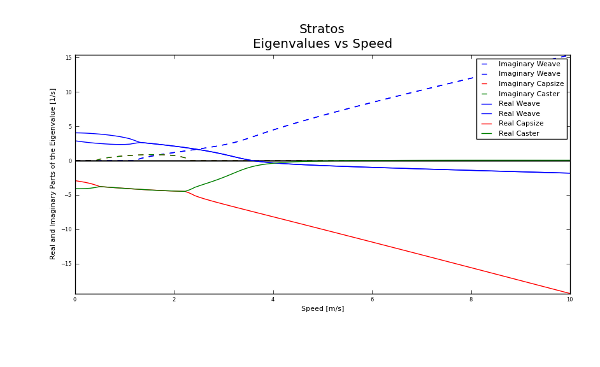
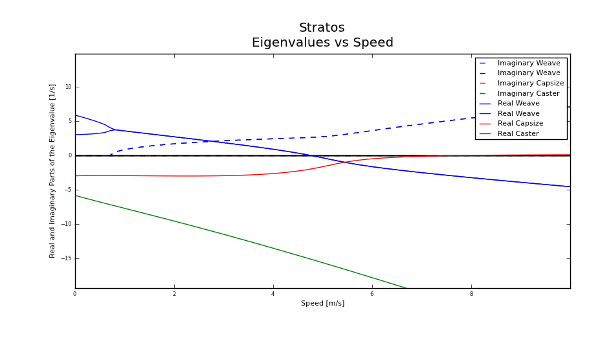
For visualization of the linear analysis you can plot the root loci of the real and imaginary parts of the eigenvalues as a function of speed:
>>> import numpy as np
>>> speeds = np.linspace(0., 10., num=100)
>>> bicycle.plot_eigenvalues_vs_speed(speeds)
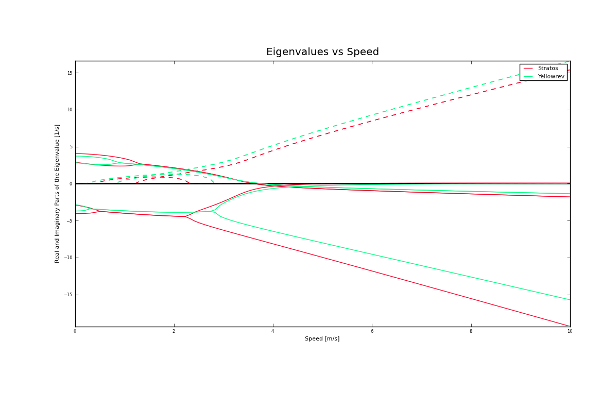
You can also compare the eigenvalues of two or more bicycles:
>>> yellowrev = bp.Bicycle('Yellowrev')
>>> bp.plot_eigenvalues([bicycle, yellowrev], speeds)
Tables¶
You can generate reStructuredText tables of the bicycle parameters with the Table class:
>>> from bicycleparameters import tables
>>> tab = tables.Table('Measured', False, bicycle, yellowrev)
>>> rst = tab.create_rst_table()
>>> print rst
+----------+------------------+------------------+
| | Stratos | Yellowrev |
+==========+=========+========+=========+========+
| Variable | v | sigma | v | sigma |
+----------+---------+--------+---------+--------+
| IBxx | 0.373 | 0.002 | 0.2254 | 0.0009 |
+----------+---------+--------+---------+--------+
| IBxz | -0.0383 | 0.0004 | 0.0179 | 0.0001 |
+----------+---------+--------+---------+--------+
| IByy | 0.717 | 0.003 | 0.388 | 0.005 |
+----------+---------+--------+---------+--------+
| IBzz | 0.455 | 0.002 | 0.2147 | 0.0009 |
+----------+---------+--------+---------+--------+
| IFxx | 0.0916 | 0.0004 | 0.0852 | 0.0003 |
+----------+---------+--------+---------+--------+
| IFyy | 0.157 | 0.001 | 0.147 | 0.002 |
+----------+---------+--------+---------+--------+
| IHxx | 0.1768 | 0.0008 | 0.1475 | 0.0006 |
+----------+---------+--------+---------+--------+
| IHxz | -0.0273 | 0.0006 | -0.0172 | 0.0005 |
+----------+---------+--------+---------+--------+
| IHyy | 0.144 | 0.002 | 0.120 | 0.002 |
+----------+---------+--------+---------+--------+
| IHzz | 0.0446 | 0.0003 | 0.0294 | 0.0004 |
+----------+---------+--------+---------+--------+
| IRxx | 0.0939 | 0.0004 | 0.0877 | 0.0004 |
+----------+---------+--------+---------+--------+
| IRyy | 0.154 | 0.001 | 0.149 | 0.001 |
+----------+---------+--------+---------+--------+
| c | 0.056 | 0.002 | 0.180 | 0.002 |
+----------+---------+--------+---------+--------+
| g | 9.81 | 0.01 | 9.81 | 0.01 |
+----------+---------+--------+---------+--------+
| lam | 0.295 | 0.003 | 0.339 | 0.003 |
+----------+---------+--------+---------+--------+
| mB | 7.22 | 0.02 | 3.31 | 0.02 |
+----------+---------+--------+---------+--------+
| mF | 3.33 | 0.02 | 1.90 | 0.02 |
+----------+---------+--------+---------+--------+
| mH | 3.04 | 0.02 | 2.45 | 0.02 |
+----------+---------+--------+---------+--------+
| mR | 3.96 | 0.02 | 2.57 | 0.02 |
+----------+---------+--------+---------+--------+
| rF | 0.3400 | 0.0001 | 0.3419 | 0.0001 |
+----------+---------+--------+---------+--------+
| rR | 0.3385 | 0.0001 | 0.3414 | 0.0001 |
+----------+---------+--------+---------+--------+
| w | 1.037 | 0.002 | 0.985 | 0.002 |
+----------+---------+--------+---------+--------+
| xB | 0.326 | 0.003 | 0.412 | 0.004 |
+----------+---------+--------+---------+--------+
| xH | 0.911 | 0.004 | 0.919 | 0.005 |
+----------+---------+--------+---------+--------+
| zB | -0.483 | 0.003 | -0.618 | 0.004 |
+----------+---------+--------+---------+--------+
| zH | -0.730 | 0.002 | -0.816 | 0.002 |
+----------+---------+--------+---------+--------+
Which renders in Sphinx like:
| Stratos | Yellowrev | |||
|---|---|---|---|---|
| Variable | v | sigma | v | sigma |
| IBxx | 0.373 | 0.002 | 0.2254 | 0.0009 |
| IBxz | -0.0383 | 0.0004 | 0.0179 | 0.0001 |
| IByy | 0.717 | 0.003 | 0.388 | 0.005 |
| IBzz | 0.455 | 0.002 | 0.2147 | 0.0009 |
| IFxx | 0.0916 | 0.0004 | 0.0852 | 0.0003 |
| IFyy | 0.157 | 0.001 | 0.147 | 0.002 |
| IHxx | 0.1768 | 0.0008 | 0.1475 | 0.0006 |
| IHxz | -0.0273 | 0.0006 | -0.0172 | 0.0005 |
| IHyy | 0.144 | 0.002 | 0.120 | 0.002 |
| IHzz | 0.0446 | 0.0003 | 0.0294 | 0.0004 |
| IRxx | 0.0939 | 0.0004 | 0.0877 | 0.0004 |
| IRyy | 0.154 | 0.001 | 0.149 | 0.001 |
| c | 0.056 | 0.002 | 0.180 | 0.002 |
| g | 9.81 | 0.01 | 9.81 | 0.01 |
| lam | 0.295 | 0.003 | 0.339 | 0.003 |
| mB | 7.22 | 0.02 | 3.31 | 0.02 |
| mF | 3.33 | 0.02 | 1.90 | 0.02 |
| mH | 3.04 | 0.02 | 2.45 | 0.02 |
| mR | 3.96 | 0.02 | 2.57 | 0.02 |
| rF | 0.3400 | 0.0001 | 0.3419 | 0.0001 |
| rR | 0.3385 | 0.0001 | 0.3414 | 0.0001 |
| w | 1.037 | 0.002 | 0.985 | 0.002 |
| xB | 0.326 | 0.003 | 0.412 | 0.004 |
| xH | 0.911 | 0.004 | 0.919 | 0.005 |
| zB | -0.483 | 0.003 | -0.618 | 0.004 |
| zH | -0.730 | 0.002 | -0.816 | 0.002 |
Rigid Rider¶
The program also allows one to add the inertial affects of a rigid rider to the Whipple bicycle system.
Rider Data¶
You can provide rider data in one of two ways, much in the same way as the bicycle. If you have the inertial parameters of a rider, e.g. Jason, simply add a file into the ./riders/Jason/Parameters/ directory. Or if you have raw measurements of the rider add the two files to ./riders/Jason/RawData/. The yeadon documentation explains how to collect the data for a rider.
Adding a Rider¶
To add a rider key in:
>>> bicycle.add_rider('Jason')
The program first looks for a parameter for for Jason sitting on the Stratos and if it can’t find one, it looks for the raw data for Jason and computes the inertial parameters. You can force calculation from raw data with:
>>> bicycle.add_rider('Jason', reCalc=True)
Exploring the rider¶
The bicycle has a few new attributes now that it has a rider:
>>> bicycle.hasRider
True
>>> bicycle.riderName
'Jason'
>>> bicycle.riderPar # inertial parmeters of the rider
{'Benchmark': {'IBxx': 7.8188533619237681,
'IBxz': -0.035425693766513083,
'IByy': 8.2729669089020437,
'IBzz': 2.354736583109867,
'mB': 79.152920866435153,
'xB': 0.46614935153554904,
'yB': 2.1457815736317352e-07,
'zB': -1.0385521459829261}}
>>> bicycle.human # this is a yeadon.human object representing the Jason
<yeadon.human.human instance at 0x2b19dd0>
The bicycle parameters now reflect that a rigid rider has been added to the bicycle frame:
>>> bicycle.parameters['Benchmark']['mB']
86.37292086643515+/-0.02
At this point, the uncertainties don’t necessarily offer much information for any of the parameters that are functions of the rider, because we do not have a good idea of the uncertainty in the human inertia calculations in the Yeadon method.
Analysis¶
The same linear analysis can be performed now that a rider has been added, albeit the reported values and graphs will reflect the fact that the bicycle frame has the added inertial effects of the rider.
Plots¶
The bicycle geometry plot now reflects that there is a rider on the bicycle and displays a simplified depiction:
>>> bicycle.plot_bicycle_geometry()
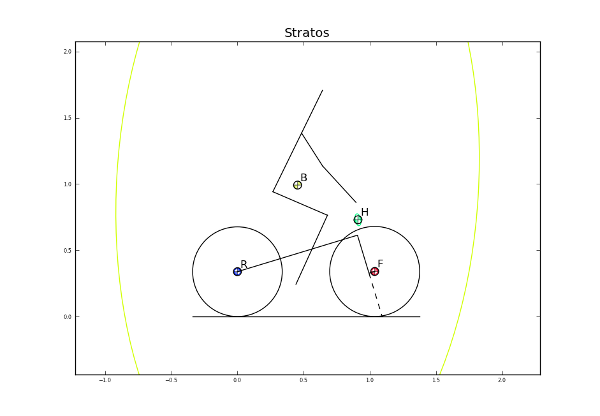
The eigenvalue plot also relfects the changes:
>>> bicycle.plot_eigenvalues_vs_speed(speeds)
Rider Visualization¶
If you have the optional dependency, visual python, for yeadon installed then you can output a three dimensional picture of the Yeadon model configured to be seated on the bicycle. This is a bit buggy due to the nature of visual python, but is useful none-the-less.:
>>> bicycle.add_rider('Jason', draw=True)
