Insert-Overlapping Performance

The tests measure the performance of sets and dicts with integer keys. The following implementation are compared:

• banyan_red_black_tree - banyan.SortedSet or banyan.SortedDict with key_type = int or key_type = str and alg = banyan.RED_BLACK_TREE
• banyan_splay_tree - banyan.SortedSet or banyan.SortedDict with key_type = int or key_type = str and alg = banyan.SPLAY_TREE
• banyan_sorted_list - banyan.SortedSet or banyan.SortedDict with key_type = int or key_type = str and alg = banyan.SORTEDLISt
• banyan_red_black_tree_gen - banyan.SortedSet or banyan.SortedDict without key-type specification and alg = banyan.RED_BLACK_TREE
• banyan_splay_tree_gen - banyan.SortedSet or banyan.SortedDict without key-type specification and alg = banyan.SPLAY_TREE
• banyan_sorted_list_gen - banyan.SortedSet or banyan.SortedDict without key-type specification alg = banyan.SORTEDLISt
• bintrees - A bintrees.FastRBTree (V 1.0.1) red-black tree.
• blist - A blist.sortedset (V 1.3.4) BTree
• btrees - A BTrees.OOBTree (V 4.0.5) BTree
• bx - A bx (V 0.7.1) tree
• dict - Python’s (hash-based) dict
• set - Python’s (hash-based) set

The following figure shows the running time of inserting integer intervals one by one into a set and, and finding the intervals overlapping the inserted interval after each insertion, as a function of the number of intervals (see _set_insert_overlapping_intervals.py for the source). It primarily shows the effect of key-type specificication:

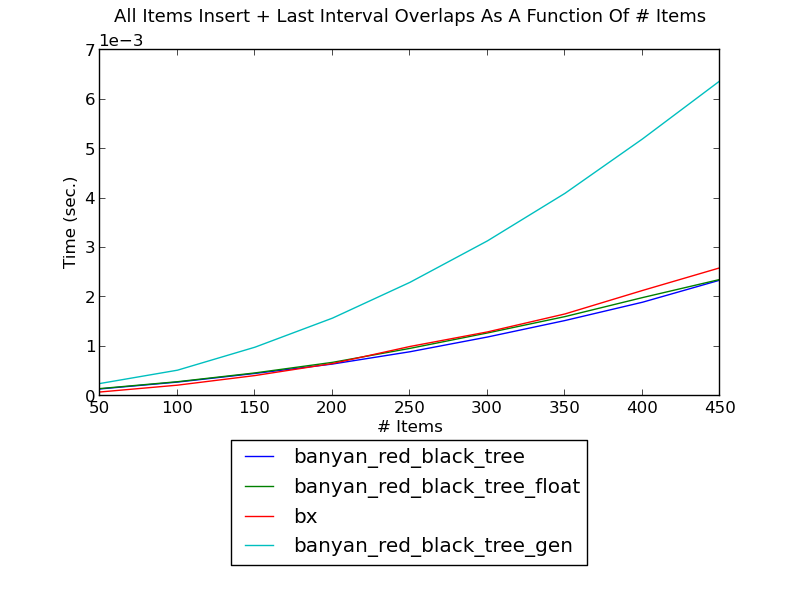
The faster Banyan implementations here are those which specify the key types, e.g.,

>>> # An integer-interval tree
>>> t = SortedSet(key_type = (int, int), updator = OverlappingIntervalsUpdator)
>>>
>>> # A float-interval tree
>>> t = SortedSet(key_type = (float, float), updator = OverlappingIntervalsUpdator)

following that is the bx implementation, which presumably uses some homogeneous keys internally as well. The slowest Banyan implementation is due to its flexibility: without key-type specification, “intervals” of any type can be used, e.g.,

>>> SortedSet([('a', 'aa'), ('bb', 'mmm')], updator = OverlappingIntervalsUpdator).overlap_point('a')
[('a', 'aa')]

This flexibility comes with a performance penalty.