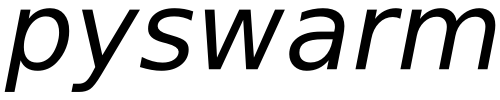
The pyswarm package is a gradient-free, evolutionary optimization package for python that supports constraints.
The package currently includes a single function for performing PSO: pso. It is both Python2 and Python3 compatible.
The installation commands below should be run in a DOS or Unix command shell (not in a Python shell).
Under Windows (version 7 and earlier), a command shell can be obtained by running cmd.exe (through the Run… menu item from the Start menu). Under Unix (Linux, Mac OS X,…), a Unix shell is available when opening a terminal (in Mac OS X, the Terminal program is found in the Utilities folder, which can be accessed through the Go menu in the Finder).
One of the automatic installation or upgrade procedures below might work on your system, if you have a Python package installer or use certain Linux distributions.
Under Unix, it may be necessary to prefix the commands below with sudo, so that the installation program has sufficient access rights to the system.
If you have pip, you can try to install the latest version with
pip install --upgrade pyswarm
If you have setuptools, you can try to automatically install or upgrade this package with
easy_install --upgrade pyswarm
Alternatively, you can simply download the package archive from the Python Package Index (PyPI) and unpack it. The package can then be installed by going into the unpacked directory (pyswarm-...), and running the provided setup.py program with
python setup.py install
or, for an installation in the user Python library (no additional access rights needed):
python setup.py install --user
or, for an installation in a custom directory my_directory:
python setup.py install --install-lib my_directory
or, if additional access rights are needed (Unix):
sudo python setup.py install
You can also simply move the pyswarm-py* directory that corresponds best to your version of Python to a location that Python can import from (directory in which scripts using pyswarm are run, etc.); the chosen pyswarm-py* directory should then be renamed pyswarm. Python 3 users should then run 2to3 -w . from inside this directory so as to automatically adapt the code to Python 3.
The latest, bleeding-edge but working code and documentation source are available on GitHub.
To illustrate how pyswarm is to be best utilized, we’ll start with a complete example, which will be explained step-by-step afterwards:
from pyswarm import pso
def banana(x):
x1 = x[0]
x2 = x[1]
return x1**4 - 2*x2*x1**2 + x2**2 + x1**2 - 2*x1 + 5
def con(x):
x1 = x[0]
x2 = x[1]
return [-(x1 + 0.25)**2 + 0.75*x2]
lb = [-3, -1]
ub = [2, 6]
xopt, fopt = pso(banana, lb, ub, f_ieqcons=con)
# Optimum should be around x=[0.5, 0.76] with banana(x)=4.5 and con(x)=0
Now let’s walk through each section of code. We start off with any necessary imports, in this case it’s just the optimizer function pso:
from pyswarm import pso
Then we define the objective function to be minimized, which should be defined like myfunction(x, *args, **kwargs). In other words, it takes as its first argument an 1-d array-like object, followed by any other (optional) arguments and (again, optional) keyword arguments. The function should return a single scalar value that is minimized. In this example, the banana function:
def banana(x):
x1 = x[0]
x2 = x[1]
return x1**4 - 2*x2*x1**2 + x2**2 + x1**2 - 2*x1 + 5
Optimizing with constraints is optional, but we include one here to illustrate how it might be done in the con function which has the same call syntax as the objective, but returns an array of values (even if it only has a single value in it):
def con(x):
x1 = x[0]
x2 = x[1]
return [-(x1 + 0.25)**2 + 0.75*x2]
Rather than specify a starting point for the algorithm, we define the limits of the input variables that the optimizer is allowed to search within. For the sake of clarity, we have defined them prior to calling the optimizer in the objects lb and ub, which stand for lower-bound and upper-bound, respectively:
lb = [-3, -1]
ub = [2, 6]
That is really all that needs to be defined to run pso, so we then call the optimizer:
xopt, fopt = pso(banana, lb, ub, f_ieqcons=con)
Using the kwarg f_ieqcons tells the routine that there’s a single constraint function that returns an array object.
Once complete, pso returns two objects: 1) the optimal input values and 2) the optimal objective value.
The full call syntax for pso is highly customizable and is defined as follows:
pso(func, lb, ub, ieqcons=[], f_ieqcons=None, args=(), kwargs={},
swarmsize=100, omega=0.5, phip=0.5, phig=0.5, maxiter=100, minstep=1e-8,
minfunc=1e-8, debug=False)
where the minimum required input arguments are:
- func : function
- The function to be minimized
- lb : array
- The lower bounds of the design variable(s)
- ub : array
- The upper bounds of the design variable(s)
and the optional input keyword-arguments are defined as:
- ieqcons : list
- A list of functions of length n such that ieqcons[j](x,*args) >= 0.0 in a successfully optimized problem (Default: empty list, [])
- f_ieqcons : function
- Returns a 1-D array in which each element must be greater or equal to 0.0 in a successfully optimized problem. If f_ieqcons is specified, ieqcons is ignored (Default: None)
- args : tuple
- Additional arguments passed to objective and constraint functions (Default: empty tuple, ())
- kwargs : dict
- Additional keyword arguments passed to objective and constraint functions (Default: empty dict, {})
- swarmsize : int
- The number of particles in the swarm (Default: 100)
- omega : scalar
- Particle velocity scaling factor (Default: 0.5)
- phip : scalar
- Scaling factor to search away from the particle’s best known position (Default: 0.5)
- phig : scalar
- Scaling factor to search away from the swarm’s best known position (Default: 0.5)
- maxiter : int
- The maximum number of iterations for the swarm to search (Default: 100)
- minstep : scalar
- The minimum stepsize of swarm’s best position before the search terminates (Default: 1e-8)
- minfunc : scalar
- The minimum change of swarm’s best objective value before the search terminates (Default: 1e-8)
- debug : boolean
- If True, progress statements will be displayed every iteration (Default: False)
We could have written the constraint function to return a scalar value instead of an array-like object, like:
def con(x):
x1 = x[0]
x2 = x[1]
return -(x1 + 0.25)**2 + 0.75*x2
In which case, we would have utilized the keyword-argument ieqcons, which takes an array of function handles, like:
xopt, fopt = pso(banana, lb, ub, ieqcons=[con])
The parameters args and kwargs are used to pass any additional parameters to the objective and constraint functions and are not changed during the optimization process.
The parameters omega, phig and phip are a way of controlling how closely the particles move away from their own best known position and the best known position of all the particles in the swarm. These can take any scalar value, but values between 0 and 1 seem to work best.
Finally, the parameters maxiter, minstep and minfunc are used to tell the swarm when to stop searching. The last parameter debug can be used to print out progress statements about the swarm.
Another useful example is in the design of a two-bar truss in the shape of an A-frame. The objective of the problem is to minimize the weight of the truss while satisfying three design constraints:
The design variables are:
Other parameters that will be held constant are:
This example shows how the optional args parameter may be used to pass other needed values to the objective and constraint functions. The complete code is as follows:
import numpy as np
from pyswarm import pso
# Define the objective (to be minimize)
def weight(x, *args):
H, d, t = x
B, rho, E, P = args
return rho*2*np.pi*d*t*np.sqrt((B/2)**2 + H**2)
# Setup the constraint functions
def yield_stress(x, *args):
H, d, t = x
B, rho, E, P = args
return (P*np.sqrt((B/2)**2 + H**2))/(2*t*np.pi*d*H)
def buckling_stress(x, *args):
H, d, t = x
B, rho, E, P = args
return (np.pi**2*E*(d**2 + t**2))/(8*((B/2)**2 + H**2))
def deflection(x, *args):
H, d, t = x
B, rho, E, P = args
return (P*np.sqrt((B/2)**2 + H**2)**3)/(2*t*np.pi*d*H**2*E)
def constraints(x, *args):
strs = yield_stress(x, *args)
buck = buckling_stress(x, *args)
defl = deflection(x, *args)
return [100 - strs, buck - strs, 0.25 - defl]
# Define the other parameters
B = 60 # inches
rho = 0.3 # lb/in^3
E = 30000 # kpsi (1000-psi)
P = 66 # kip (1000-lbs, force)
args = (B, rho, E, P)
# Define the lower and upper bounds for H, d, t, respectively
lb = [10, 1, 0.01]
ub = [30, 3, 0.25]
xopt, fopt = pso(weight, lb, ub, f_ieqcons=constraints, args=args)
# The optimal input values are approximately
# xopt = [29, 2.4, 0.06]
# with function values approximately
# weight = 12 lbs
# yield stress = 100 kpsi (binding constraint)
# buckling stress = 150 kpsi
# deflection = 0.2 in
Because there’s an aspect of randomness in the algorithm, it is common to get a slightly different result each time it is run. This is to be expected.
Keeping everything else the same, we could have also defined the constraints using ieqcons like this:
...
# Setup the constraint functions
def yield_stress(x, *args):
H, d, t = x
B, rho, E, P = args
strs = (P*np.sqrt((B/2)**2 + H**2))/(2*t*np.pi*d*H)
return 100 - strs
def buckling_stress(x, *args):
H, d, t = x
B, rho, E, P = args
buck = (np.pi**2*E*(d**2 + t**2))/(8*((B/2)**2 + H**2))
strs = yield_stress(x, *args)
return buck - strs
def deflection(x, *args):
H, d, t = x
B, rho, E, P = args
defl = (P*np.sqrt((B/2)**2 + H**2)**3)/(2*t*np.pi*d*H**2*E)
return 0.25 - defl
...
cons = [yield_stress, buckling_stress, deflection]
...
xopt, fopt = pso(weight, lb, ub, ieqcons=cons, args=args)
And this would function the same way as the prior formulation. Use whichever way works best for your application!
Any feedback, questions, bug reports, or success stores should be sent to the author. I’d love to hear from you!
This package is provided under two licenses: