Belief Functions

class improb.lowprev.belfunc.BelFunc(pspace=None, mapping=None, lprev=None, uprev=None, prev=None, lprob=None, uprob=None, prob=None, bba=None, credalset=None, number_type=None)

Bases: improb.lowprev.lowprob.LowProb

A belief function, implemented as a LowProb, except that it uses the Mobius transform to calculate the natural extension; see get_lower().

See also

improb.lowprev.lowprob.LowProb.is_completely_monotone()

To check for complete monotonicity.

get_lower(gamble, event=True, algorithm='mobius')

Calculate the lower expectation of a gamble.

The default algorithm is to use the Mobius transform 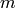of the lower probability :

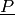See also

improb.setfunction.SetFunction.get_bba_choquet()

Find Choquet integral via Mobius transform of an arbitrary set function.

Warning

To use the Mobius transform, the domain of the lower probability must contain all events. If needed, call extend():

>>> bel = BelFunc(2, lprob=['0.2', '0.25']) 
>>> print(bel)
0   : 1/5
  1 : 1/4
>>> bel.get_lower([1, 3]) # oops! fails... 
Traceback (most recent call last):
    ...
KeyError: ...
>>> # solve linear program instead of trying Mobius transform
>>> bel.get_lower([1, 3], algorithm='linprog') # 1 * 0.75 + 3 * 0.25 = 1.5
Fraction(3, 2)
>>> bel.extend()
>>> print(bel)
    : 0
0   : 1/5
  1 : 1/4
0 1 : 1
>>> # now try with Mobius transform; should give same result
>>> bel.get_lower([1, 3]) # now it works
Fraction(3, 2)

Warning

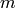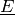With the Mobius algorithm, this method will not raise an exception even if the assessments are not completely monotone, or even incoherent—the Mobius transform is in such case still defined, although some of the values of will be negative. In fact, if the assessments are not 2-monotone, then will be incoherent as well.

>>> bel = BelFunc(
...     pspace='abcd',
...     lprob={'ab': '0.2', 'bc': '0.2', 'abc': '0.2', 'b': '0.1'})
>>> bel.extend()
>>> bel.is_n_monotone(2)
False
>>> # exact linear programming algorithm
>>> bel.get_lower([1, 2, 1, 0], algorithm='linprog')
Fraction(2, 5)
>>> # mobius algorithm: different result!!
>>> bel.get_lower([1, 2, 1, 0])
Fraction(3, 10)

>>> from improb.lowprev.belfunc import BelFunc
>>> from improb.lowprev.lowprob import LowProb
>>> from improb import PSpace
>>> pspace = PSpace(2)
>>> lowprob = LowProb(pspace, lprob=['0.3', '0.2'])
>>> lowprob.extend()
>>> lowprob.is_completely_monotone()
True
>>> print(lowprob)
    : 0
0   : 3/10
  1 : 1/5
0 1 : 1
>>> print(lowprob.mobius)
    : 0
0   : 3/10
  1 : 1/5
0 1 : 1/2
>>> lpr = BelFunc(pspace, bba=lowprob.mobius)
>>> lpr.is_completely_monotone()
True
>>> print(lpr)
    : 0
0   : 3/10
  1 : 1/5
0 1 : 1
>>> print(lpr.mobius)
    : 0
0   : 3/10
  1 : 1/5
0 1 : 1/2
>>> print(lpr.get_lower([1,0]))
3/10
>>> print(lpr.get_lower([0,1]))
1/5
>>> print(lpr.get_lower([4,9])) # 0.8 * 4 + 0.2 * 9
5
>>> print(lpr.get_lower([5,1])) # 0.3 * 5 + 0.7 * 1
11/5